From Dense to Sparse: Event Response for Enhanced Residential Load Forecasting

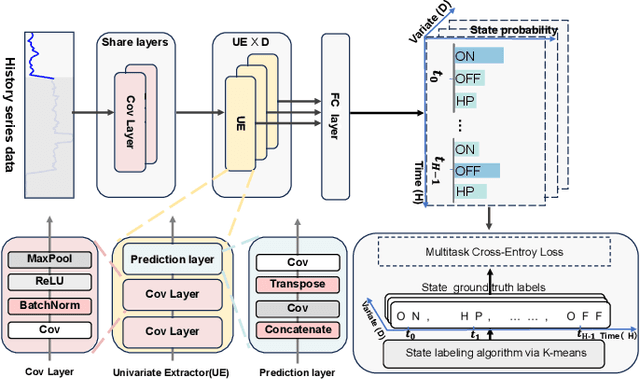
Residential load forecasting (RLF) is crucial for resource scheduling in power systems. Most existing methods utilize all given load records (dense data) to indiscriminately extract the dependencies between historical and future time series. However, there exist important regular patterns residing in the event-related associations among different appliances (sparse knowledge), which have yet been ignored. In this paper, we propose an Event-Response Knowledge Guided approach (ERKG) for RLF by incorporating the estimation of electricity usage events for different appliances, mining event-related sparse knowledge from the load series. With ERKG, the event-response estimation enables portraying the electricity consumption behaviors of residents, revealing regular variations in appliance operational states. To be specific, ERKG consists of knowledge extraction and guidance: i) a forecasting model is designed for the electricity usage events by estimating appliance operational states, aiming to extract the event-related sparse knowledge; ii) a novel knowledge-guided mechanism is established by fusing such state estimates of the appliance events into the RLF model, which can give particular focuses on the patterns of users' electricity consumption behaviors. Notably, ERKG can flexibly serve as a plug-in module to boost the capability of existing forecasting models by leveraging event response. In numerical experiments, extensive comparisons and ablation studies have verified the effectiveness of our ERKG, e.g., over 8% MAE can be reduced on the tested state-of-the-art forecasting models.

DDoS: Diffusion Distribution Similarity for Out-of-Distribution Detection

Out-of-Distribution (OoD) detection determines whether the given samples are from the training distribution of the classifier-under-protection, i.e., the In-Distribution (InD), or from a different OoD. Latest researches introduce diffusion models pre-trained on InD data to advocate OoD detection by transferring an OoD image into a generated one that is close to InD, so that one could capture the distribution disparities between original and generated images to detect OoD data. Existing diffusion-based detectors adopt perceptual metrics on the two images to measure such disparities, but ignore a fundamental fact: Perceptual metrics are devised essentially for human-perceived similarities of low-level image patterns, e.g., textures and colors, and are not advisable in evaluating distribution disparities, since images with different low-level patterns could possibly come from the same distribution. To address this issue, we formulate a diffusion-based detection framework that considers the distribution similarity between a tested image and its generated counterpart via a novel proper similarity metric in the informative feature space and probability space learned by the classifier-under-protection. An anomaly-removal strategy is further presented to enlarge such distribution disparities by removing abnormal OoD information in the feature space to facilitate the detection. Extensive empirical results unveil the insufficiency of perceptual metrics and the effectiveness of our distribution similarity framework with new state-of-the-art detection performance.

Learning in Feature Spaces via Coupled Covariances: Asymmetric Kernel SVD and Nyström method

In contrast with Mercer kernel-based approaches as used e.g., in Kernel Principal Component Analysis (KPCA), it was previously shown that Singular Value Decomposition (SVD) inherently relates to asymmetric kernels and Asymmetric Kernel Singular Value Decomposition (KSVD) has been proposed. However, the existing formulation to KSVD cannot work with infinite-dimensional feature mappings, the variational objective can be unbounded, and needs further numerical evaluation and exploration towards machine learning. In this work, i) we introduce a new asymmetric learning paradigm based on coupled covariance eigenproblem (CCE) through covariance operators, allowing infinite-dimensional feature maps. The solution to CCE is ultimately obtained from the SVD of the induced asymmetric kernel matrix, providing links to KSVD. ii) Starting from the integral equations corresponding to a pair of coupled adjoint eigenfunctions, we formalize the asymmetric Nystr\"om method through a finite sample approximation to speed up training. iii) We provide the first empirical evaluations verifying the practical utility and benefits of KSVD and compare with methods resorting to symmetrization or linear SVD across multiple tasks.

Revisiting Random Weight Perturbation for Efficiently Improving Generalization

Improving the generalization ability of modern deep neural networks (DNNs) is a fundamental challenge in machine learning. Two branches of methods have been proposed to seek flat minima and improve generalization: one led by sharpness-aware minimization (SAM) minimizes the worst-case neighborhood loss through adversarial weight perturbation (AWP), and the other minimizes the expected Bayes objective with random weight perturbation (RWP). While RWP offers advantages in computation and is closely linked to AWP on a mathematical basis, its empirical performance has consistently lagged behind that of AWP. In this paper, we revisit the use of RWP for improving generalization and propose improvements from two perspectives: i) the trade-off between generalization and convergence and ii) the random perturbation generation. Through extensive experimental evaluations, we demonstrate that our enhanced RWP methods achieve greater efficiency in enhancing generalization, particularly in large-scale problems, while also offering comparable or even superior performance to SAM. The code is released at https://github.com/nblt/mARWP.

Sparsity via Sparse Group $k$-max Regularization

For the linear inverse problem with sparsity constraints, the $l_0$ regularized problem is NP-hard, and existing approaches either utilize greedy algorithms to find almost-optimal solutions or to approximate the $l_0$ regularization with its convex counterparts. In this paper, we propose a novel and concise regularization, namely the sparse group $k$-max regularization, which can not only simultaneously enhance the group-wise and in-group sparsity, but also casts no additional restraints on the magnitude of variables in each group, which is especially important for variables at different scales, so that it approximate the $l_0$ norm more closely. We also establish an iterative soft thresholding algorithm with local optimality conditions and complexity analysis provided. Through numerical experiments on both synthetic and real-world datasets, we verify the effectiveness and flexibility of the proposed method.

Kernel PCA for Out-of-Distribution Detection

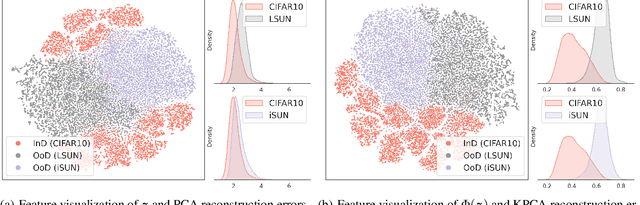
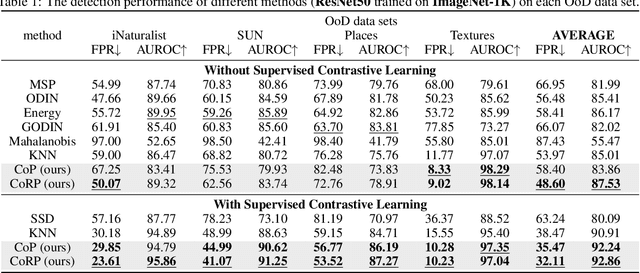
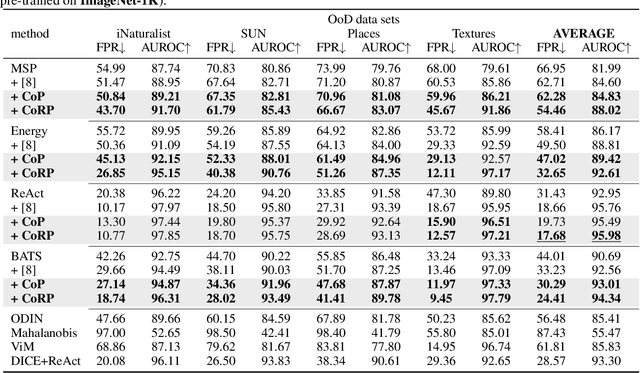
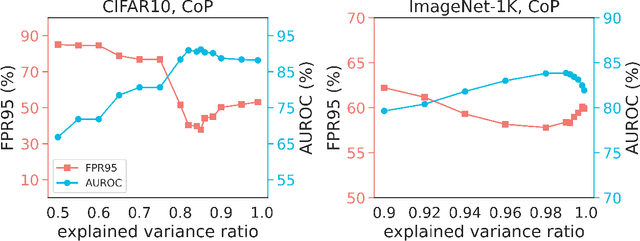
Out-of-Distribution (OoD) detection is vital for the reliability of Deep Neural Networks (DNNs). Existing works have shown the insufficiency of Principal Component Analysis (PCA) straightforwardly applied on the features of DNNs in detecting OoD data from In-Distribution (InD) data. The failure of PCA suggests that the network features residing in OoD and InD are not well separated by simply proceeding in a linear subspace, which instead can be resolved through proper nonlinear mappings. In this work, we leverage the framework of Kernel PCA (KPCA) for OoD detection, seeking subspaces where OoD and InD features are allocated with significantly different patterns. We devise two feature mappings that induce non-linear kernels in KPCA to advocate the separability between InD and OoD data in the subspace spanned by the principal components. Given any test sample, the reconstruction error in such subspace is then used to efficiently obtain the detection result with $\mathcal{O}(1)$ time complexity in inference. Extensive empirical results on multiple OoD data sets and network structures verify the superiority of our KPCA-based detector in efficiency and efficacy with state-of-the-art OoD detection performances.

Self-Attention through Kernel-Eigen Pair Sparse Variational Gaussian Processes

While the great capability of Transformers significantly boosts prediction accuracy, it could also yield overconfident predictions and require calibrated uncertainty estimation, which can be commonly tackled by Gaussian processes (GPs). Existing works apply GPs with symmetric kernels under variational inference to the attention kernel; however, omitting the fact that attention kernels are in essence asymmetric. Moreover, the complexity of deriving the GP posteriors remains high for large-scale data. In this work, we propose Kernel-Eigen Pair Sparse Variational Gaussian Processes (KEP-SVGP) for building uncertainty-aware self-attention where the asymmetry of attention kernels is tackled by Kernel SVD (KSVD) and a reduced complexity is acquired. Through KEP-SVGP, i) the SVGP pair induced by the two sets of singular vectors from KSVD w.r.t. the attention kernel fully characterizes the asymmetry; ii) using only a small set of adjoint eigenfunctions from KSVD, the derivation of SVGP posteriors can be based on the inversion of a diagonal matrix containing singular values, contributing to a reduction in time complexity; iii) an evidence lower bound is derived so that variational parameters can be optimized towards this objective. Experiments verify our excellent performances and efficiency on in-distribution, distribution-shift and out-of-distribution benchmarks.

Revisiting Deep Ensemble for Out-of-Distribution Detection: A Loss Landscape Perspective

Existing Out-of-Distribution (OoD) detection methods address to detect OoD samples from In-Distribution data (InD) mainly by exploring differences in features, logits and gradients in Deep Neural Networks (DNNs). We in this work propose a new perspective upon loss landscape and mode ensemble to investigate OoD detection. In the optimization of DNNs, there exist many local optima in the parameter space, or namely modes. Interestingly, we observe that these independent modes, which all reach low-loss regions with InD data (training and test data), yet yield significantly different loss landscapes with OoD data. Such an observation provides a novel view to investigate the OoD detection from the loss landscape and further suggests significantly fluctuating OoD detection performance across these modes. For instance, FPR values of the RankFeat method can range from 46.58% to 84.70% among 5 modes, showing uncertain detection performance evaluations across independent modes. Motivated by such diversities on OoD loss landscape across modes, we revisit the deep ensemble method for OoD detection through mode ensemble, leading to improved performance and benefiting the OoD detector with reduced variances. Extensive experiments covering varied OoD detectors and network structures illustrate high variances across modes and also validate the superiority of mode ensemble in boosting OoD detection. We hope this work could attract attention in the view of independent modes in the OoD loss landscape and more reliable evaluations on OoD detectors.

Low-Rank Multitask Learning based on Tensorized SVMs and LSSVMs

Multitask learning (MTL) leverages task-relatedness to enhance performance. With the emergence of multimodal data, tasks can now be referenced by multiple indices. In this paper, we employ high-order tensors, with each mode corresponding to a task index, to naturally represent tasks referenced by multiple indices and preserve their structural relations. Based on this representation, we propose a general framework of low-rank MTL methods with tensorized support vector machines (SVMs) and least square support vector machines (LSSVMs), where the CP factorization is deployed over the coefficient tensor. Our approach allows to model the task relation through a linear combination of shared factors weighted by task-specific factors and is generalized to both classification and regression problems. Through the alternating optimization scheme and the Lagrangian function, each subproblem is transformed into a convex problem, formulated as a quadratic programming or linear system in the dual form. In contrast to previous MTL frameworks, our decision function in the dual induces a weighted kernel function with a task-coupling term characterized by the similarities of the task-specific factors, better revealing the explicit relations across tasks in MTL. Experimental results validate the effectiveness and superiority of our proposed methods compared to existing state-of-the-art approaches in MTL. The code of implementation will be available at https://github.com/liujiani0216/TSVM-MTL.

Nonlinear SVD with Asymmetric Kernels: feature learning and asymmetric Nyström method

Asymmetric data naturally exist in real life, such as directed graphs. Different from the common kernel methods requiring Mercer kernels, this paper tackles the asymmetric kernel-based learning problem. We describe a nonlinear extension of the matrix Singular Value Decomposition through asymmetric kernels, namely KSVD. First, we construct two nonlinear feature mappings w.r.t. rows and columns of the given data matrix. The proposed optimization problem maximizes the variance of each mapping projected onto the subspace spanned by the other, subject to a mutual orthogonality constraint. Through Lagrangian duality, we show that it can be solved by the left and right singular vectors in the feature space induced by the asymmetric kernel. Moreover, we start from the integral equations with a pair of adjoint eigenfunctions corresponding to the singular vectors on an asymmetrical kernel, and extend the Nystr\"om method to asymmetric cases through the finite sample approximation, which can be applied to speedup the training in KSVD. Experiments show that asymmetric KSVD learns features outperforming Mercer-kernel based methods that resort to symmetrization, and also verify the effectiveness of the asymmetric Nystr\"om method.