Kernel PCA for Out-of-Distribution Detection

Out-of-Distribution (OoD) detection is vital for the reliability of Deep Neural Networks (DNNs). Existing works have shown the insufficiency of Principal Component Analysis (PCA) straightforwardly applied on the features of DNNs in detecting OoD data from In-Distribution (InD) data. The failure of PCA suggests that the network features residing in OoD and InD are not well separated by simply proceeding in a linear subspace, which instead can be resolved through proper nonlinear mappings. In this work, we leverage the framework of Kernel PCA (KPCA) for OoD detection, seeking subspaces where OoD and InD features are allocated with significantly different patterns. We devise two feature mappings that induce non-linear kernels in KPCA to advocate the separability between InD and OoD data in the subspace spanned by the principal components. Given any test sample, the reconstruction error in such subspace is then used to efficiently obtain the detection result with $\mathcal{O}(1)$ time complexity in inference. Extensive empirical results on multiple OoD data sets and network structures verify the superiority of our KPCA-based detector in efficiency and efficacy with state-of-the-art OoD detection performances.

Learn What You Need in Personalized Federated Learning

Personalized federated learning aims to address data heterogeneity across local clients in federated learning. However, current methods blindly incorporate either full model parameters or predefined partial parameters in personalized federated learning. They fail to customize the collaboration manner according to each local client's data characteristics, causing unpleasant aggregation results. To address this essential issue, we propose $\textit{Learn2pFed}$, a novel algorithm-unrolling-based personalized federated learning framework, enabling each client to adaptively select which part of its local model parameters should participate in collaborative training. The key novelty of the proposed $\textit{Learn2pFed}$ is to optimize each local model parameter's degree of participant in collaboration as learnable parameters via algorithm unrolling methods. This approach brings two benefits: 1) mathmatically determining the participation degree of local model parameters in the federated collaboration, and 2) obtaining more stable and improved solutions. Extensive experiments on various tasks, including regression, forecasting, and image classification, demonstrate that $\textit{Learn2pFed}$ significantly outperforms previous personalized federated learning methods.

One-shot Distributed Algorithm for Generalized Eigenvalue Problem

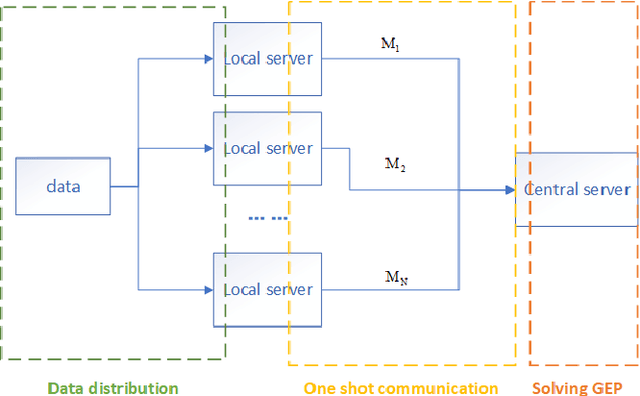
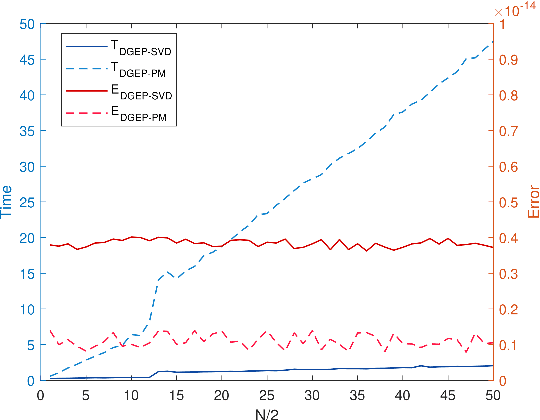
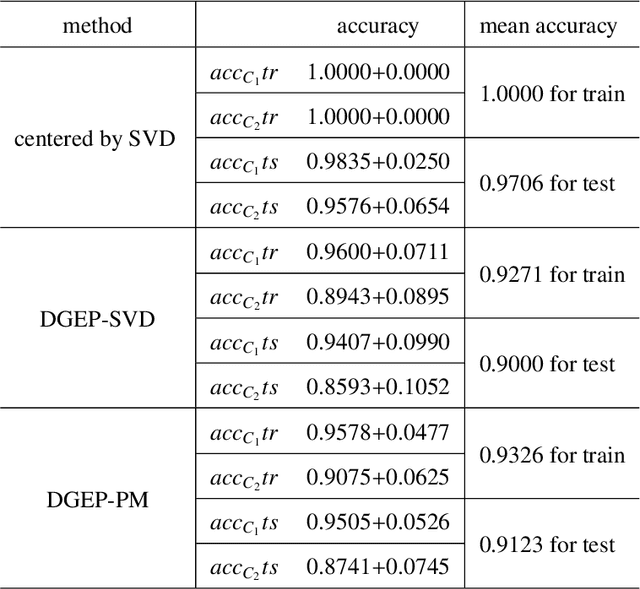
Nowadays, more and more datasets are stored in a distributed way for the sake of memory storage or data privacy. The generalized eigenvalue problem (GEP) plays a vital role in a large family of high-dimensional statistical models. However, the existing distributed method for eigenvalue decomposition cannot be applied in GEP for the divergence of the empirical covariance matrix. Here we propose a general distributed GEP framework with one-shot communication for GEP. If the symmetric data covariance has repeated eigenvalues, e.g., in canonical component analysis, we further modify the method for better convergence. The theoretical analysis on approximation error is conducted and the relation to the divergence of the data covariance, the eigenvalues of the empirical data covariance, and the number of local servers is analyzed. Numerical experiments also show the effectiveness of the proposed algorithms.

A Communication-Efficient Distributed Algorithm for Kernel Principal Component Analysis

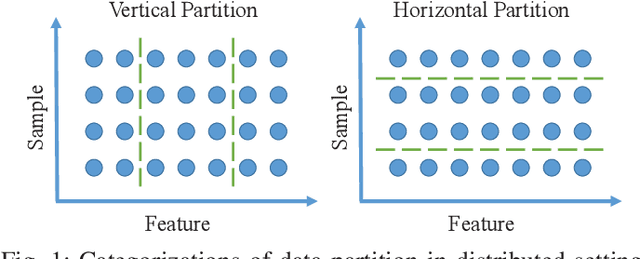
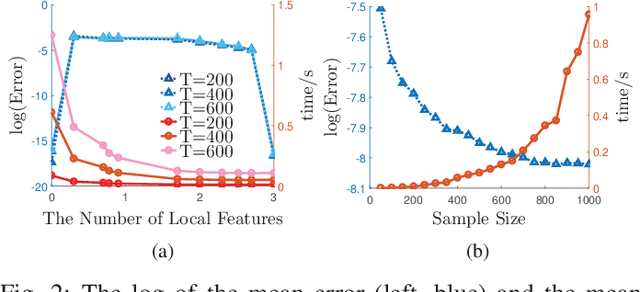
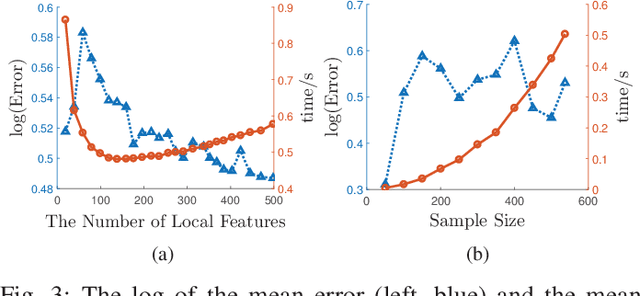
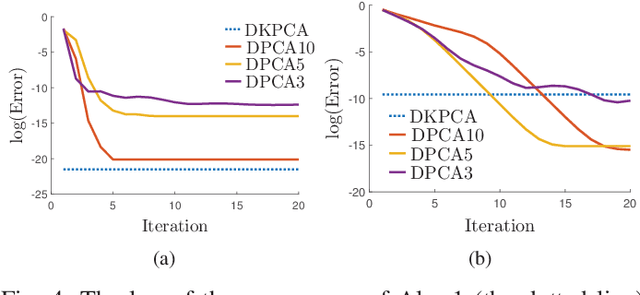
Principal Component Analysis (PCA) is a fundamental technology in machine learning. Nowadays many high-dimension large datasets are acquired in a distributed manner, which precludes the use of centralized PCA due to the high communication cost and privacy risk. Thus, many distributed PCA algorithms are proposed, most of which, however, focus on linear cases. To efficiently extract non-linear features, this brief proposes a communication-efficient distributed kernel PCA algorithm, where linear and RBF kernels are applied. The key is to estimate the global empirical kernel matrix from the eigenvectors of local kernel matrices. The approximate error of the estimators is theoretically analyzed for both linear and RBF kernels. The result suggests that when eigenvalues decay fast, which is common for RBF kernels, the proposed algorithm gives high quality results with low communication cost. Results of simulation experiments verify our theory analysis and experiments on GSE2187 dataset show the effectiveness of the proposed algorithm.

Sparse Generalized Canonical Correlation Analysis: Distributed Alternating Iteration based Approach

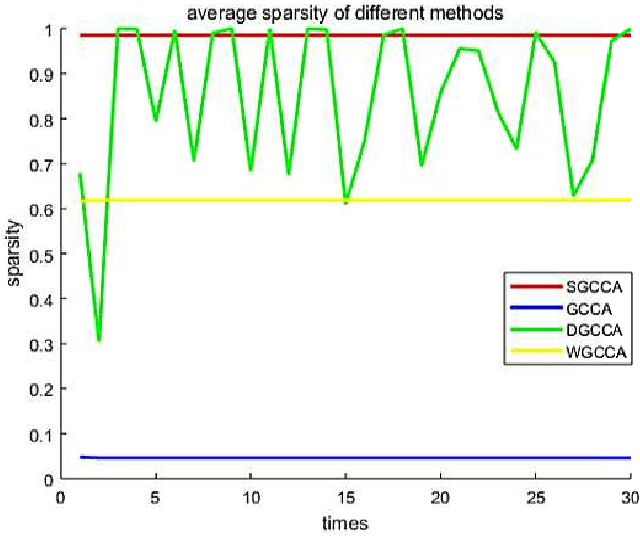
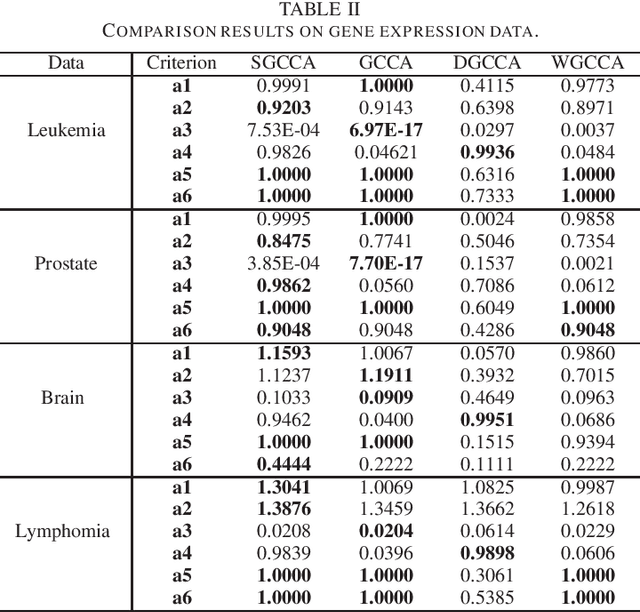
Sparse canonical correlation analysis (CCA) is a useful statistical tool to detect latent information with sparse structures. However, sparse CCA works only for two datasets, i.e., there are only two views or two distinct objects. To overcome this limitation, in this paper, we propose a sparse generalized canonical correlation analysis (GCCA), which could detect the latent relations of multiview data with sparse structures. Moreover, the introduced sparsity could be considered as Laplace prior on the canonical variates. Specifically, we convert the GCCA into a linear system of equations and impose $\ell_1$ minimization penalty for sparsity pursuit. This results in a nonconvex problem on Stiefel manifold, which is difficult to solve. Motivated by Boyd's consensus problem, an algorithm based on distributed alternating iteration approach is developed and theoretical consistency analysis is investigated elaborately under mild conditions. Experiments on several synthetic and real world datasets demonstrate the effectiveness of the proposed algorithm.