Kernel PCA for Out-of-Distribution Detection
Paper and Code
Feb 05, 2024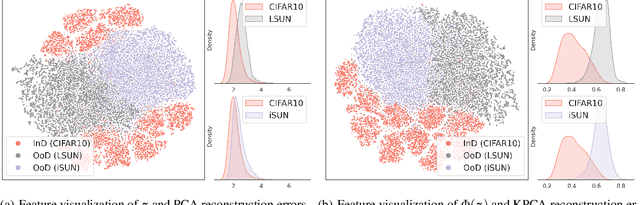
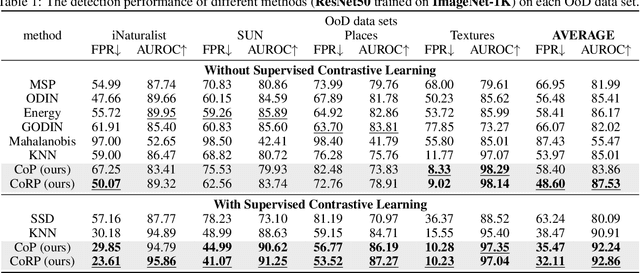
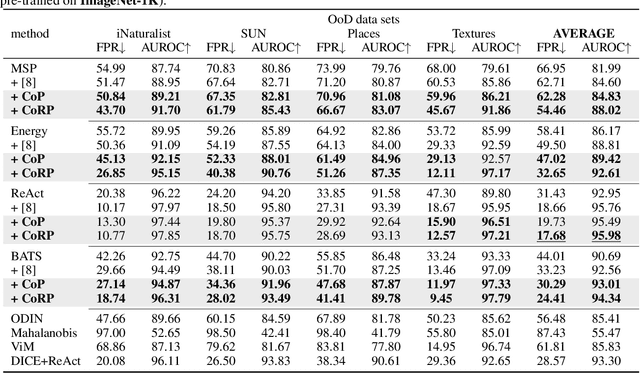
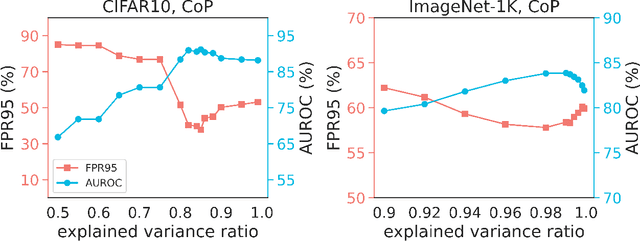
Out-of-Distribution (OoD) detection is vital for the reliability of Deep Neural Networks (DNNs). Existing works have shown the insufficiency of Principal Component Analysis (PCA) straightforwardly applied on the features of DNNs in detecting OoD data from In-Distribution (InD) data. The failure of PCA suggests that the network features residing in OoD and InD are not well separated by simply proceeding in a linear subspace, which instead can be resolved through proper nonlinear mappings. In this work, we leverage the framework of Kernel PCA (KPCA) for OoD detection, seeking subspaces where OoD and InD features are allocated with significantly different patterns. We devise two feature mappings that induce non-linear kernels in KPCA to advocate the separability between InD and OoD data in the subspace spanned by the principal components. Given any test sample, the reconstruction error in such subspace is then used to efficiently obtain the detection result with $\mathcal{O}(1)$ time complexity in inference. Extensive empirical results on multiple OoD data sets and network structures verify the superiority of our KPCA-based detector in efficiency and efficacy with state-of-the-art OoD detection performances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge