Fan He
Learning Analysis of Kernel Ridgeless Regression with Asymmetric Kernel Learning
Jun 03, 2024



Abstract:Ridgeless regression has garnered attention among researchers, particularly in light of the ``Benign Overfitting'' phenomenon, where models interpolating noisy samples demonstrate robust generalization. However, kernel ridgeless regression does not always perform well due to the lack of flexibility. This paper enhances kernel ridgeless regression with Locally-Adaptive-Bandwidths (LAB) RBF kernels, incorporating kernel learning techniques to improve performance in both experiments and theory. For the first time, we demonstrate that functions learned from LAB RBF kernels belong to an integral space of Reproducible Kernel Hilbert Spaces (RKHSs). Despite the absence of explicit regularization in the proposed model, its optimization is equivalent to solving an $\ell_0$-regularized problem in the integral space of RKHSs, elucidating the origin of its generalization ability. Taking an approximation analysis viewpoint, we introduce an $l_q$-norm analysis technique (with $0<q<1$) to derive the learning rate for the proposed model under mild conditions. This result deepens our theoretical understanding, explaining that our algorithm's robust approximation ability arises from the large capacity of the integral space of RKHSs, while its generalization ability is ensured by sparsity, controlled by the number of support vectors. Experimental results on both synthetic and real datasets validate our theoretical conclusions.
Data Imputation by Pursuing Better Classification: A Supervised Kernel-Based Method
May 13, 2024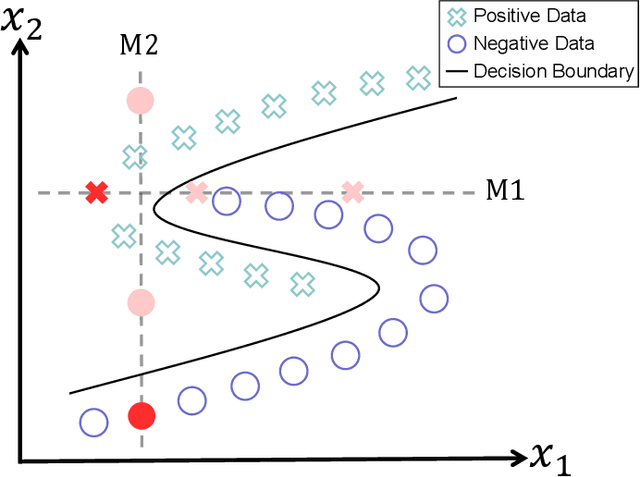
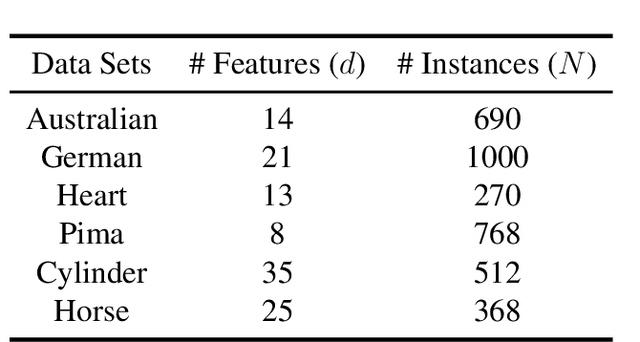

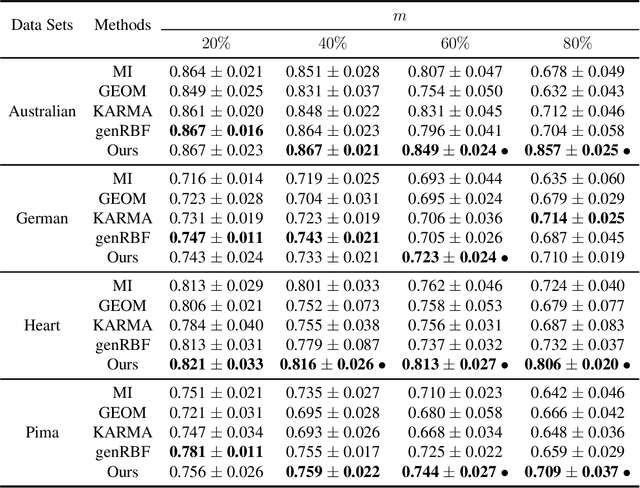
Abstract:Data imputation, the process of filling in missing feature elements for incomplete data sets, plays a crucial role in data-driven learning. A fundamental belief is that data imputation is helpful for learning performance, and it follows that the pursuit of better classification can guide the data imputation process. While some works consider using label information to assist in this task, their simplistic utilization of labels lacks flexibility and may rely on strict assumptions. In this paper, we propose a new framework that effectively leverages supervision information to complete missing data in a manner conducive to classification. Specifically, this framework operates in two stages. Firstly, it leverages labels to supervise the optimization of similarity relationships among data, represented by the kernel matrix, with the goal of enhancing classification accuracy. To mitigate overfitting that may occur during this process, a perturbation variable is introduced to improve the robustness of the framework. Secondly, the learned kernel matrix serves as additional supervision information to guide data imputation through regression, utilizing the block coordinate descent method. The superiority of the proposed method is evaluated on four real-world data sets by comparing it with state-of-the-art imputation methods. Remarkably, our algorithm significantly outperforms other methods when the data is missing more than 60\% of the features
Decentralized Kernel Ridge Regression Based on Data-dependent Random Feature
May 13, 2024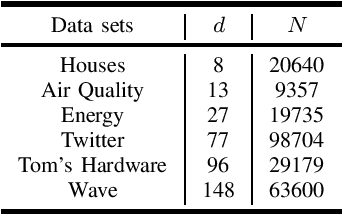
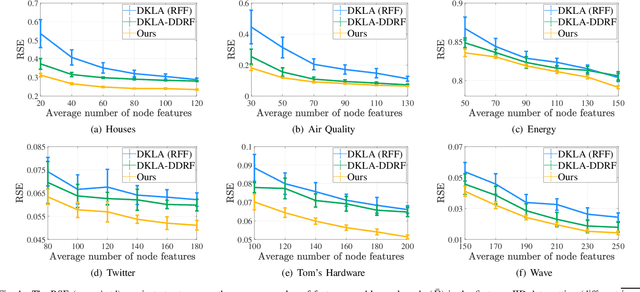
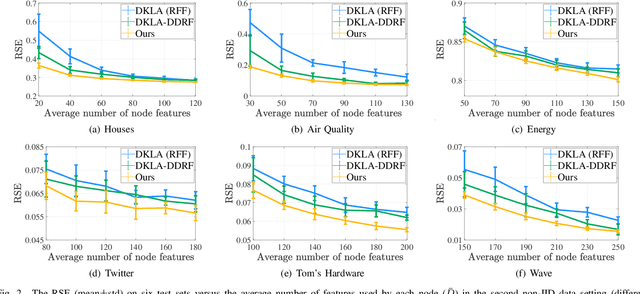
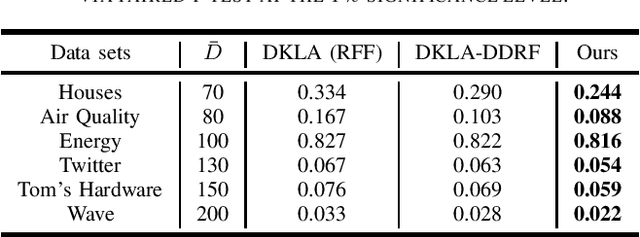
Abstract:Random feature (RF) has been widely used for node consistency in decentralized kernel ridge regression (KRR). Currently, the consistency is guaranteed by imposing constraints on coefficients of features, necessitating that the random features on different nodes are identical. However, in many applications, data on different nodes varies significantly on the number or distribution, which calls for adaptive and data-dependent methods that generate different RFs. To tackle the essential difficulty, we propose a new decentralized KRR algorithm that pursues consensus on decision functions, which allows great flexibility and well adapts data on nodes. The convergence is rigorously given and the effectiveness is numerically verified: by capturing the characteristics of the data on each node, while maintaining the same communication costs as other methods, we achieved an average regression accuracy improvement of 25.5\% across six real-world data sets.
Enhancing Kernel Flexibility via Learning Asymmetric Locally-Adaptive Kernels
Oct 08, 2023Abstract:The lack of sufficient flexibility is the key bottleneck of kernel-based learning that relies on manually designed, pre-given, and non-trainable kernels. To enhance kernel flexibility, this paper introduces the concept of Locally-Adaptive-Bandwidths (LAB) as trainable parameters to enhance the Radial Basis Function (RBF) kernel, giving rise to the LAB RBF kernel. The parameters in LAB RBF kernels are data-dependent, and its number can increase with the dataset, allowing for better adaptation to diverse data patterns and enhancing the flexibility of the learned function. This newfound flexibility also brings challenges, particularly with regards to asymmetry and the need for an efficient learning algorithm. To address these challenges, this paper for the first time establishes an asymmetric kernel ridge regression framework and introduces an iterative kernel learning algorithm. This novel approach not only reduces the demand for extensive support data but also significantly improves generalization by training bandwidths on the available training data. Experimental results on real datasets underscore the remarkable performance of the proposed algorithm, showcasing its superior capability in handling large-scale datasets compared to Nystr\"om approximation-based algorithms. Moreover, it demonstrates a significant improvement in regression accuracy over existing kernel-based learning methods and even surpasses residual neural networks.
Distilling Object Detectors With Global Knowledge
Oct 17, 2022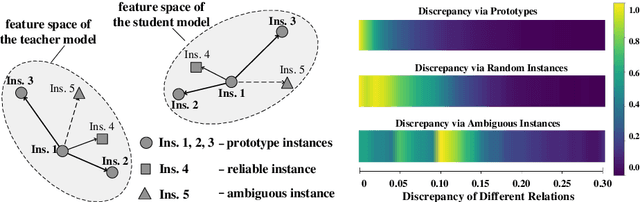
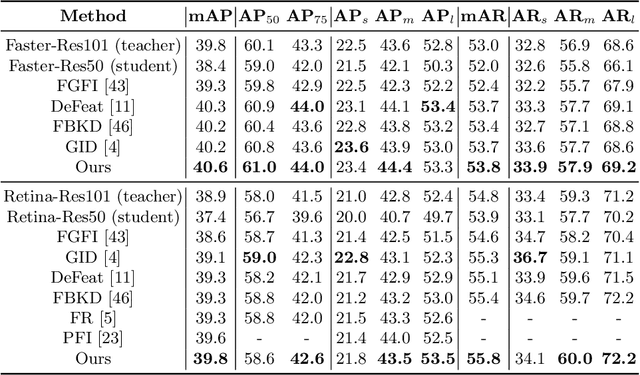
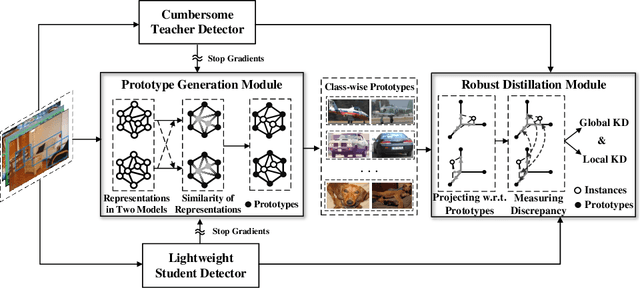
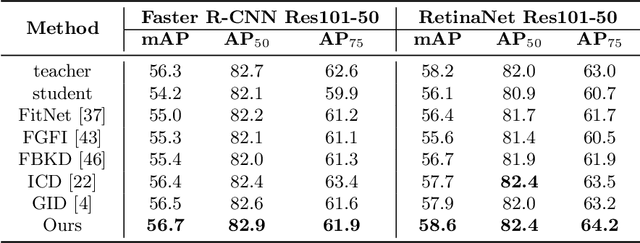
Abstract:Knowledge distillation learns a lightweight student model that mimics a cumbersome teacher. Existing methods regard the knowledge as the feature of each instance or their relations, which is the instance-level knowledge only from the teacher model, i.e., the local knowledge. However, the empirical studies show that the local knowledge is much noisy in object detection tasks, especially on the blurred, occluded, or small instances. Thus, a more intrinsic approach is to measure the representations of instances w.r.t. a group of common basis vectors in the two feature spaces of the teacher and the student detectors, i.e., global knowledge. Then, the distilling algorithm can be applied as space alignment. To this end, a novel prototype generation module (PGM) is proposed to find the common basis vectors, dubbed prototypes, in the two feature spaces. Then, a robust distilling module (RDM) is applied to construct the global knowledge based on the prototypes and filtrate noisy global and local knowledge by measuring the discrepancy of the representations in two feature spaces. Experiments with Faster-RCNN and RetinaNet on PASCAL and COCO datasets show that our method achieves the best performance for distilling object detectors with various backbones, which even surpasses the performance of the teacher model. We also show that the existing methods can be easily combined with global knowledge and obtain further improvement. Code is available: https://github.com/hikvision-research/DAVAR-Lab-ML.
Random Fourier Features for Asymmetric Kernels
Sep 18, 2022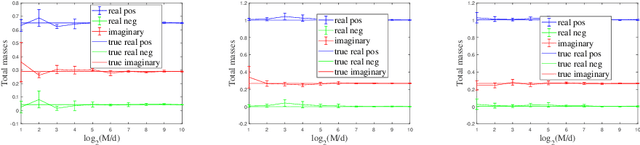
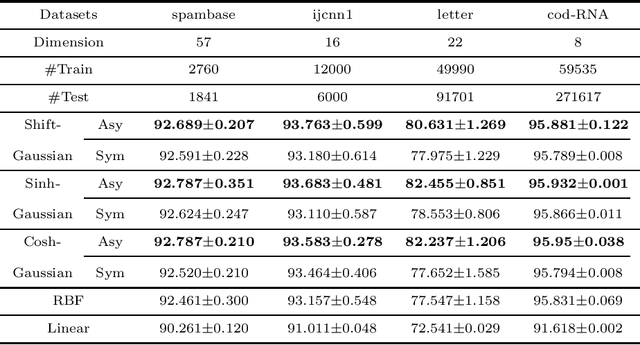
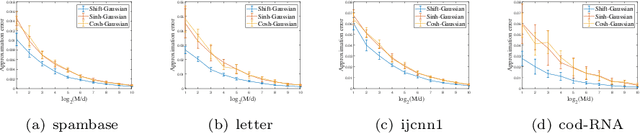
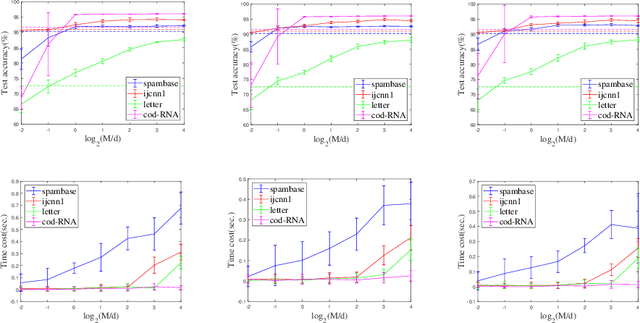
Abstract:The random Fourier features (RFFs) method is a powerful and popular technique in kernel approximation for scalability of kernel methods. The theoretical foundation of RFFs is based on the Bochner theorem that relates symmetric, positive definite (PD) functions to probability measures. This condition naturally excludes asymmetric functions with a wide range applications in practice, e.g., directed graphs, conditional probability, and asymmetric kernels. Nevertheless, understanding asymmetric functions (kernels) and its scalability via RFFs is unclear both theoretically and empirically. In this paper, we introduce a complex measure with the real and imaginary parts corresponding to four finite positive measures, which expands the application scope of the Bochner theorem. By doing so, this framework allows for handling classical symmetric, PD kernels via one positive measure; symmetric, non-positive definite kernels via signed measures; and asymmetric kernels via complex measures, thereby unifying them into a general framework by RFFs, named AsK-RFFs. Such approximation scheme via complex measures enjoys theoretical guarantees in the perspective of the uniform convergence. In algorithmic implementation, to speed up the kernel approximation process, which is expensive due to the calculation of total mass, we employ a subset-based fast estimation method that optimizes total masses on a sub-training set, which enjoys computational efficiency in high dimensions. Our AsK-RFFs method is empirically validated on several typical large-scale datasets and achieves promising kernel approximation performance, which demonstrate the effectiveness of AsK-RFFs.
Learning with Asymmetric Kernels: Least Squares and Feature Interpretation
Feb 03, 2022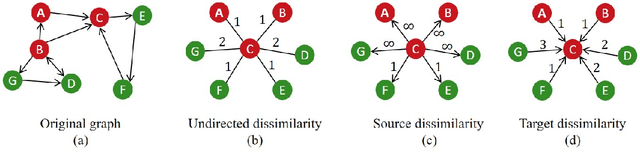
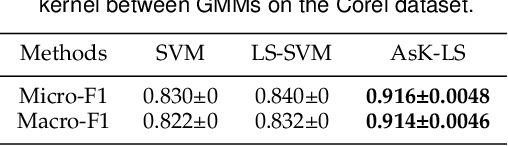
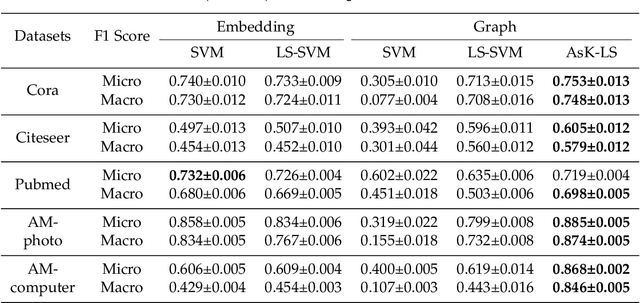
Abstract:Asymmetric kernels naturally exist in real life, e.g., for conditional probability and directed graphs. However, most of the existing kernel-based learning methods require kernels to be symmetric, which prevents the use of asymmetric kernels. This paper addresses the asymmetric kernel-based learning in the framework of the least squares support vector machine named AsK-LS, resulting in the first classification method that can utilize asymmetric kernels directly. We will show that AsK-LS can learn with asymmetric features, namely source and target features, while the kernel trick remains applicable, i.e., the source and target features exist but are not necessarily known. Besides, the computational burden of AsK-LS is as cheap as dealing with symmetric kernels. Experimental results on the Corel database, directed graphs, and the UCI database will show that in the case asymmetric information is crucial, the proposed AsK-LS can learn with asymmetric kernels and performs much better than the existing kernel methods that have to do symmetrization to accommodate asymmetric kernels.
One-shot Distributed Algorithm for Generalized Eigenvalue Problem
Oct 22, 2020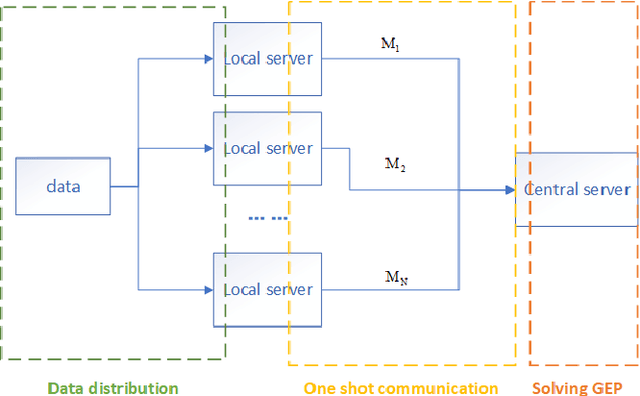
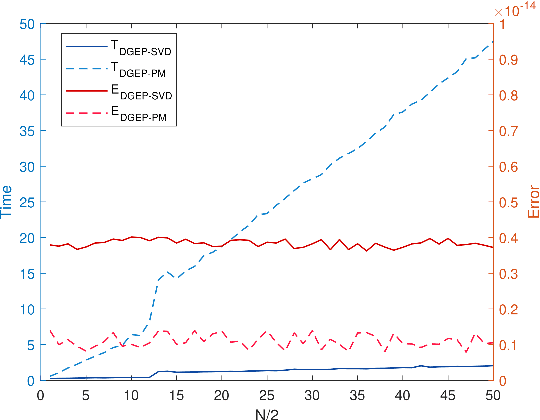
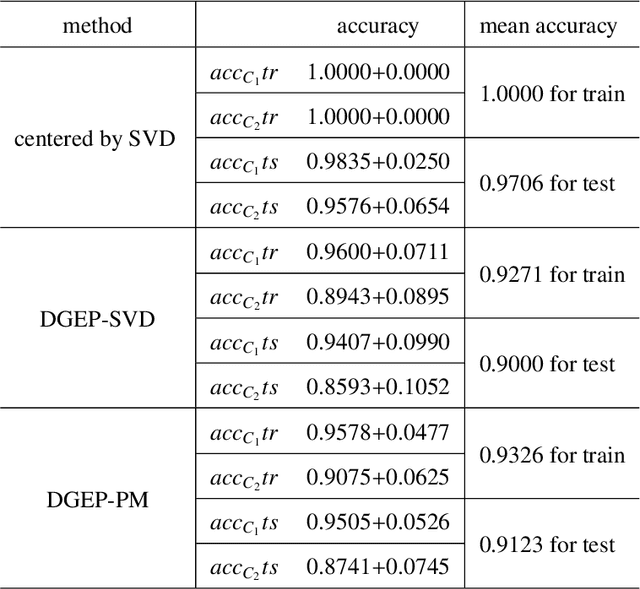

Abstract:Nowadays, more and more datasets are stored in a distributed way for the sake of memory storage or data privacy. The generalized eigenvalue problem (GEP) plays a vital role in a large family of high-dimensional statistical models. However, the existing distributed method for eigenvalue decomposition cannot be applied in GEP for the divergence of the empirical covariance matrix. Here we propose a general distributed GEP framework with one-shot communication for GEP. If the symmetric data covariance has repeated eigenvalues, e.g., in canonical component analysis, we further modify the method for better convergence. The theoretical analysis on approximation error is conducted and the relation to the divergence of the data covariance, the eigenvalues of the empirical data covariance, and the number of local servers is analyzed. Numerical experiments also show the effectiveness of the proposed algorithms.
Attack on Multi-Node Attention for Object Detection
Aug 16, 2020
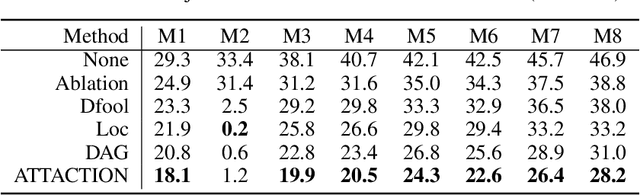
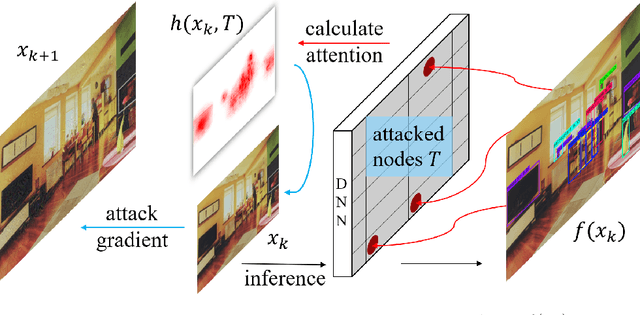
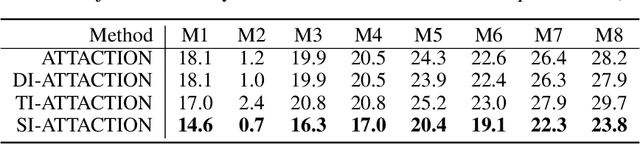
Abstract:This paper focuses on high-transferable adversarial attacks on detection networks, which are crucial for life-concerning systems such as autonomous driving and security surveillance. Detection networks are hard to attack in a black-box manner, because of their multiple-output property and diversity across architectures. To pursue a high attacking transferability, one needs to find a common property shared by different models. Multi-node attention heat map obtained by our newly proposed method is such a property. Based on it, we design the ATTACk on multi-node attenTION for object detecTION (ATTACTION). ATTACTION achieves a state-of-the-art transferability in numerical experiments. On MS COCO, the detection mAP for all 7 tested black-box architectures is halved and the performance of semantic segmentation is greatly influenced. Given the great transferability of ATTACTION, we generate Adversarial Objects in COntext (AOCO), the first adversarial dataset on object detection networks, which could help designers to quickly evaluate and improve the robustness of detection networks.
A Communication-Efficient Distributed Algorithm for Kernel Principal Component Analysis
May 06, 2020
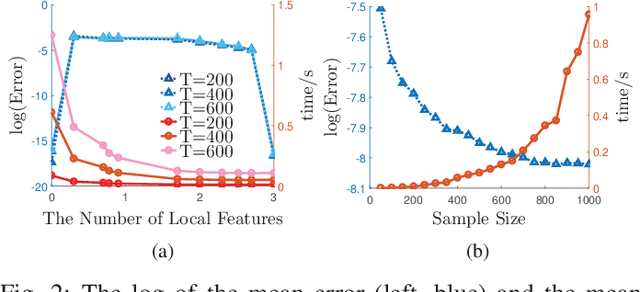
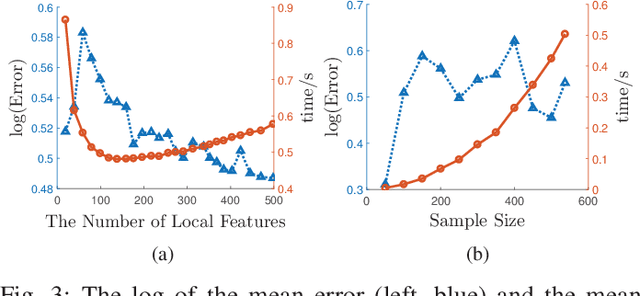
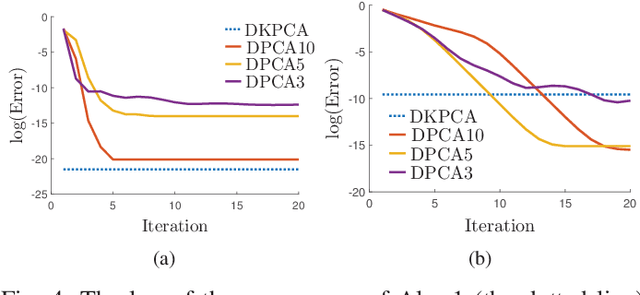
Abstract:Principal Component Analysis (PCA) is a fundamental technology in machine learning. Nowadays many high-dimension large datasets are acquired in a distributed manner, which precludes the use of centralized PCA due to the high communication cost and privacy risk. Thus, many distributed PCA algorithms are proposed, most of which, however, focus on linear cases. To efficiently extract non-linear features, this brief proposes a communication-efficient distributed kernel PCA algorithm, where linear and RBF kernels are applied. The key is to estimate the global empirical kernel matrix from the eigenvectors of local kernel matrices. The approximate error of the estimators is theoretically analyzed for both linear and RBF kernels. The result suggests that when eigenvalues decay fast, which is common for RBF kernels, the proposed algorithm gives high quality results with low communication cost. Results of simulation experiments verify our theory analysis and experiments on GSE2187 dataset show the effectiveness of the proposed algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge