One-shot Distributed Algorithm for Generalized Eigenvalue Problem
Paper and Code
Oct 22, 2020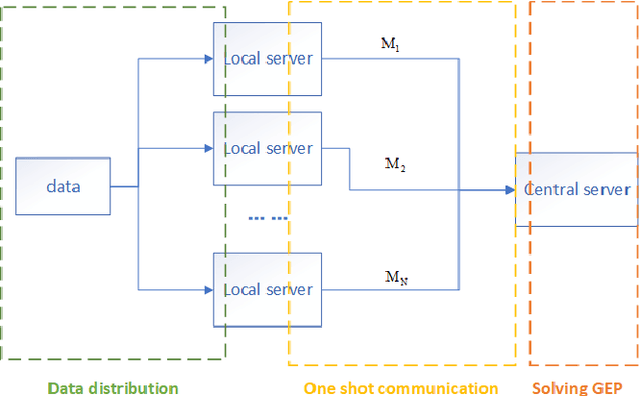
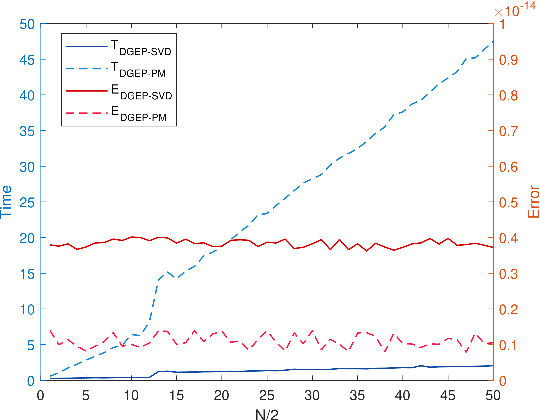
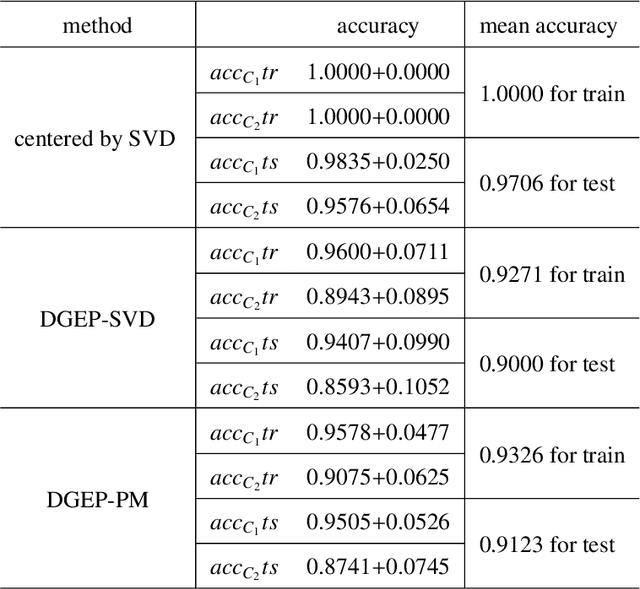

Nowadays, more and more datasets are stored in a distributed way for the sake of memory storage or data privacy. The generalized eigenvalue problem (GEP) plays a vital role in a large family of high-dimensional statistical models. However, the existing distributed method for eigenvalue decomposition cannot be applied in GEP for the divergence of the empirical covariance matrix. Here we propose a general distributed GEP framework with one-shot communication for GEP. If the symmetric data covariance has repeated eigenvalues, e.g., in canonical component analysis, we further modify the method for better convergence. The theoretical analysis on approximation error is conducted and the relation to the divergence of the data covariance, the eigenvalues of the empirical data covariance, and the number of local servers is analyzed. Numerical experiments also show the effectiveness of the proposed algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge