Astra: Toward General-Purpose Mobile Robots via Hierarchical Multimodal Learning

Modern robot navigation systems encounter difficulties in diverse and complex indoor environments. Traditional approaches rely on multiple modules with small models or rule-based systems and thus lack adaptability to new environments. To address this, we developed Astra, a comprehensive dual-model architecture, Astra-Global and Astra-Local, for mobile robot navigation. Astra-Global, a multimodal LLM, processes vision and language inputs to perform self and goal localization using a hybrid topological-semantic graph as the global map, and outperforms traditional visual place recognition methods. Astra-Local, a multitask network, handles local path planning and odometry estimation. Its 4D spatial-temporal encoder, trained through self-supervised learning, generates robust 4D features for downstream tasks. The planning head utilizes flow matching and a novel masked ESDF loss to minimize collision risks for generating local trajectories, and the odometry head integrates multi-sensor inputs via a transformer encoder to predict the relative pose of the robot. Deployed on real in-house mobile robots, Astra achieves high end-to-end mission success rate across diverse indoor environments.

Data Imputation by Pursuing Better Classification: A Supervised Kernel-Based Method

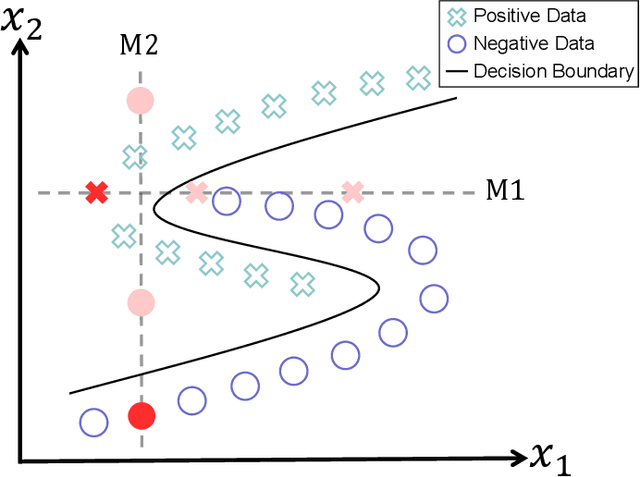
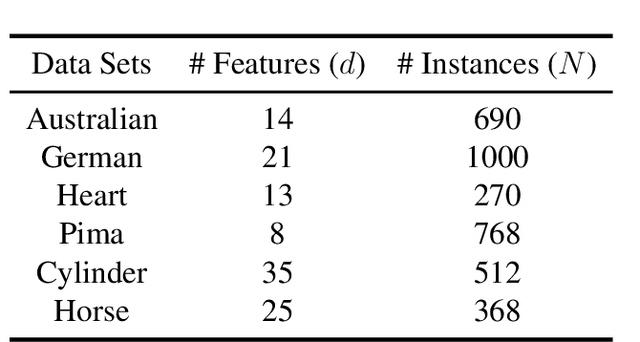
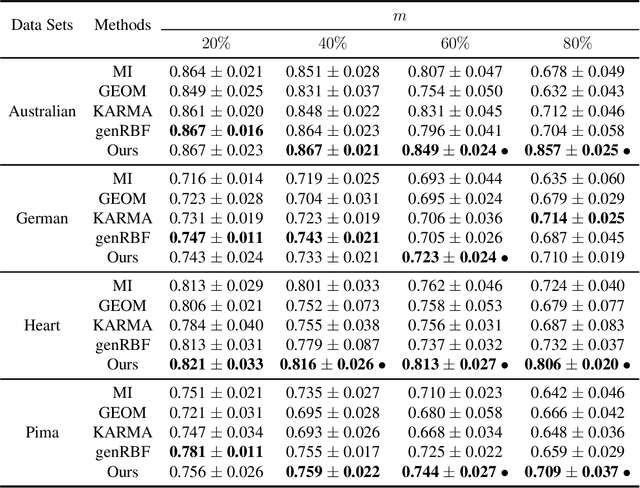
Data imputation, the process of filling in missing feature elements for incomplete data sets, plays a crucial role in data-driven learning. A fundamental belief is that data imputation is helpful for learning performance, and it follows that the pursuit of better classification can guide the data imputation process. While some works consider using label information to assist in this task, their simplistic utilization of labels lacks flexibility and may rely on strict assumptions. In this paper, we propose a new framework that effectively leverages supervision information to complete missing data in a manner conducive to classification. Specifically, this framework operates in two stages. Firstly, it leverages labels to supervise the optimization of similarity relationships among data, represented by the kernel matrix, with the goal of enhancing classification accuracy. To mitigate overfitting that may occur during this process, a perturbation variable is introduced to improve the robustness of the framework. Secondly, the learned kernel matrix serves as additional supervision information to guide data imputation through regression, utilizing the block coordinate descent method. The superiority of the proposed method is evaluated on four real-world data sets by comparing it with state-of-the-art imputation methods. Remarkably, our algorithm significantly outperforms other methods when the data is missing more than 60\% of the features

Nonasymptotic Performance Analysis of Direct-Augmentation and Spatial-Smoothing ESPRIT for Localization of More Sources Than Sensors Using Sparse Arrays

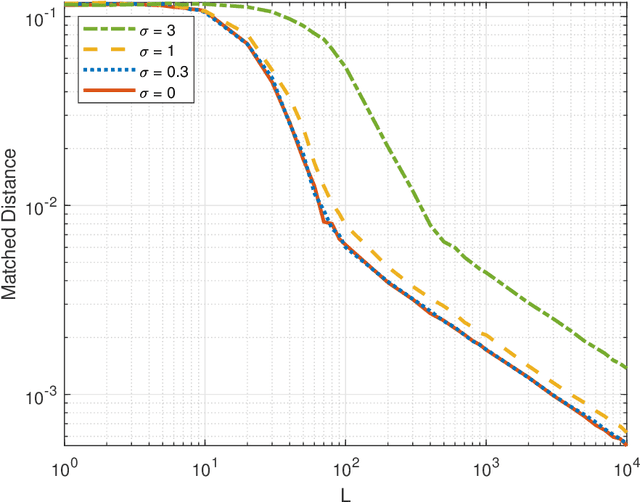
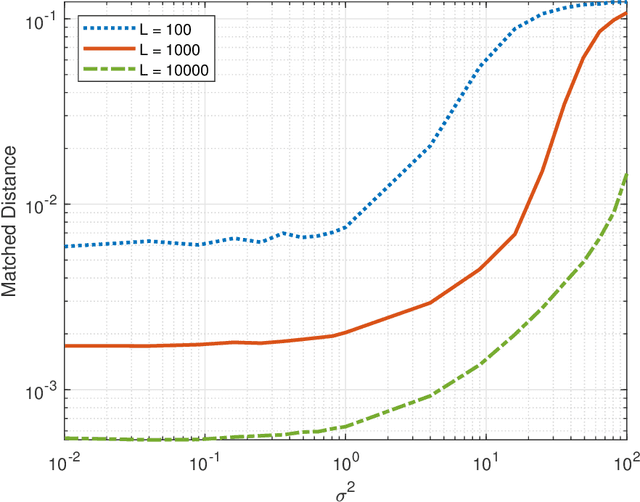
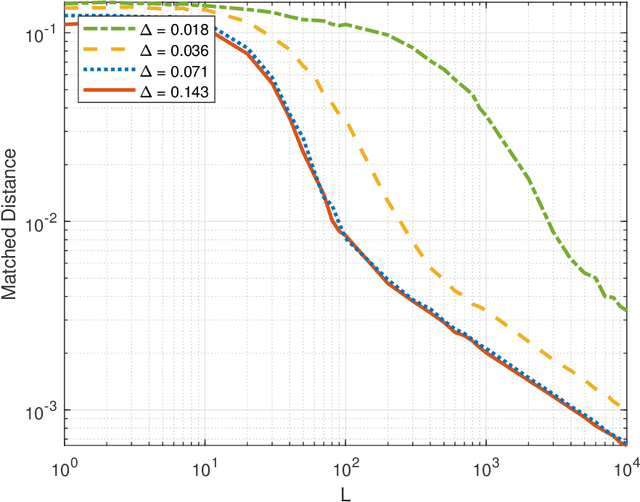
Direction augmentation (DA) and spatial smoothing (SS), followed by a subspace method such as ESPRIT or MUSIC, are two simple and successful approaches that enable localization of more uncorrelated sources than sensors with a proper sparse array. In this paper, we carry out nonasymptotic performance analyses of DA-ESPRIT and SS-ESPRIT in the practical finite-snapshot regime. We show that their absolute localization errors are bounded from above by $C_1\frac{\max\{\sigma^2, C_2\}}{\sqrt{L}}$ with overwhelming probability, where $L$ is the snapshot number, $\sigma^2$ is the Gaussian noise power, and $C_1,C_2$ are constants independent of $L$ and $\sigma^2$, if and only if they can do exact source localization with infinitely many snapshots. We also show that their resolution increases with the snapshot number, without a substantial limit. Numerical results corroborating our analysis are provided.

Deep Kernel Learning via Random Fourier Features

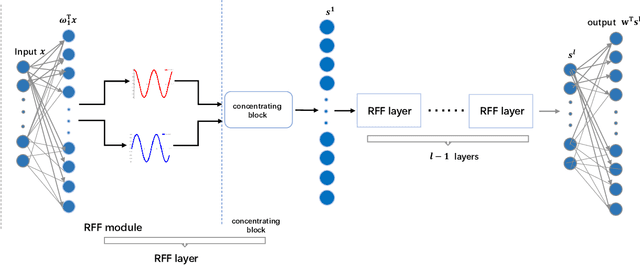
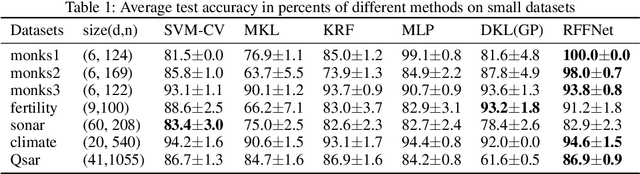
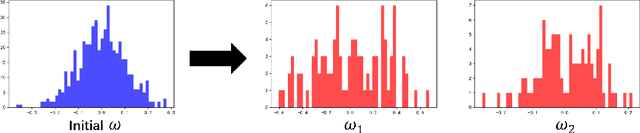
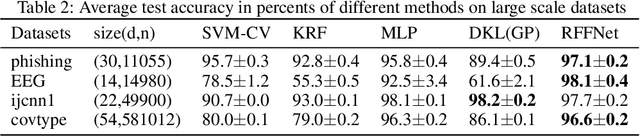
Kernel learning methods are among the most effective learning methods and have been vigorously studied in the past decades. However, when tackling with complicated tasks, classical kernel methods are not flexible or "rich" enough to describe the data and hence could not yield satisfactory performance. In this paper, via Random Fourier Features (RFF), we successfully incorporate the deep architecture into kernel learning, which significantly boosts the flexibility and richness of kernel machines while keeps kernels' advantage of pairwise handling small data. With RFF, we could establish a deep structure and make every kernel in RFF layers could be trained end-to-end. Since RFF with different distributions could represent different kernels, our model has the capability of finding suitable kernels for each layer, which is much more flexible than traditional kernel-based methods where the kernel is pre-selected. This fact also helps yield a more sophisticated kernel cascade connection in the architecture. On small datasets (less than 1000 samples), for which deep learning is generally not suitable due to overfitting, our method achieves superior performance compared to advanced kernel methods. On large-scale datasets, including non-image and image classification tasks, our method also has competitive performance.