UAV-Enabled Secure ISAC Against Dual Eavesdropping Threats: Joint Beamforming and Trajectory Design

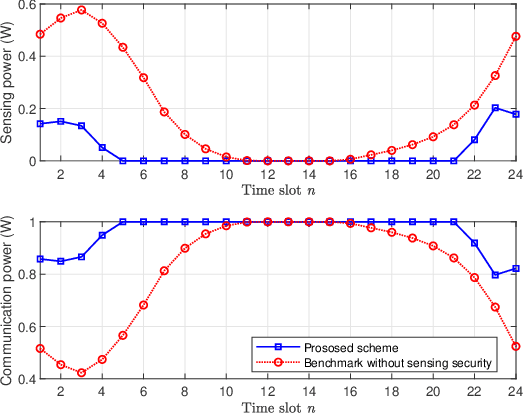
In this work, we study an unmanned aerial vehicle (UAV)-enabled secure integrated sensing and communication (ISAC) system, where a UAV serves as an aerial base station (BS) to simultaneously perform communication with a user and detect a target on the ground, while a dual-functional eavesdropper attempts to intercept the signals for both sensing and communication. Facing the dual eavesdropping threats, we aim to enhance the average achievable secrecy rate for the communication user by jointly designing the UAV trajectory together with the transmit information and sensing beamforming, while satisfying the requirements on sensing performance and sensing security, as well as the UAV power and flight constraints. To address the non-convex nature of the optimization problem, we employ the alternating optimization (AO) strategy, jointly with the successive convex approximation (SCA) and semidefinite relaxation (SDR) methods. Numerical results validate the proposed approach, demonstrating its ability to achieve a high secrecy rate while meeting the required sensing and security constraints.

Bit Efficient Toeplitz Covariance Estimation

This paper addresses the challenge of Toeplitz covariance matrix estimation from partial entries of random quantized samples. To balance trade-offs among the number of samples, the number of entries observed per sample, and the data resolution, we propose a ruler-based quantized Toeplitz covariance estimator. We derive non-asymptotic error bounds and analyze the convergence rates of the proposed estimator. Our results show that the estimator is near-optimal and imply that reducing data resolution within a certain range has a limited impact on the estimation accuracy. Numerical experiments are provided that validate our theoretical findings and show effectiveness of the proposed estimator.

RIS-aided MIMO Beamforming: Piece-Wise Near-field Channel Model

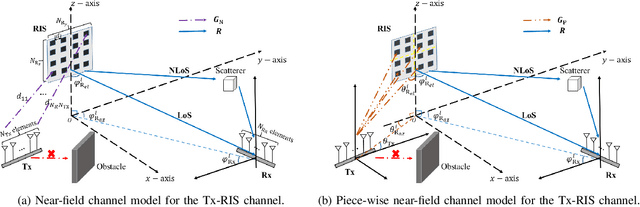
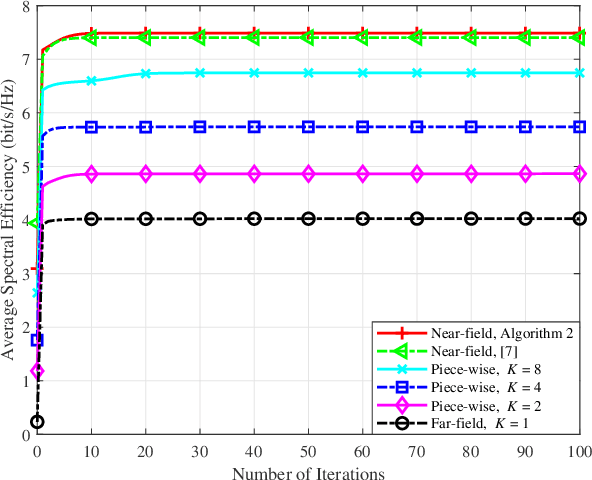
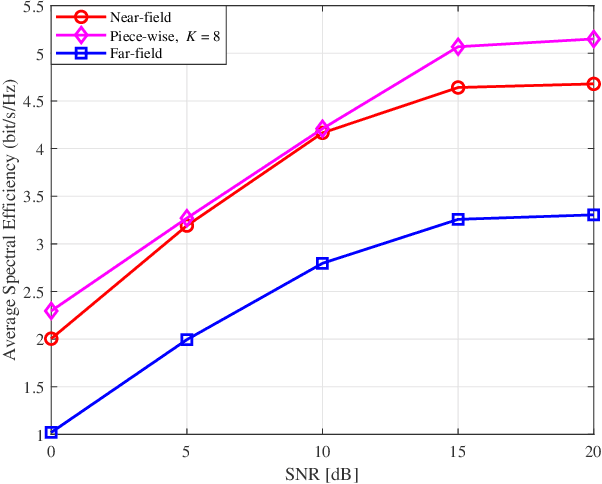
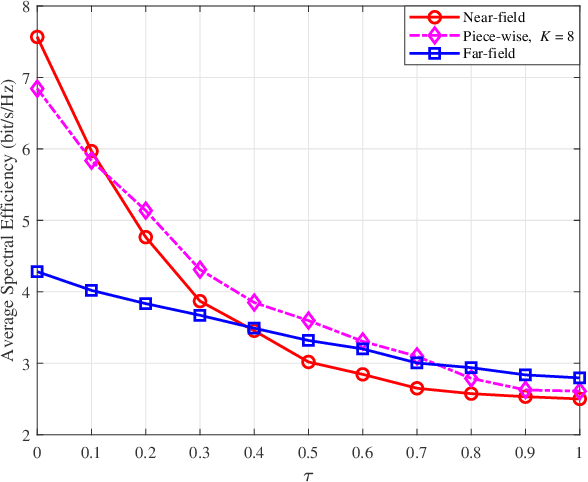
This paper proposes a joint active and passive beamforming design for reconfigurable intelligent surface (RIS)-aided wireless communication systems, adopting a piece-wise near-field channel model. While a traditional near-field channel model, applied without any approximations, offers higher modeling accuracy than a far-field model, it renders the system design more sensitive to channel estimation errors (CEEs). As a remedy, we propose to adopt a piece-wise near-field channel model that leverages the advantages of the near-field approach while enhancing its robustness against CEEs. Our study analyzes the impact of different channel models, including the traditional near-field, the proposed piece-wise near-field and far-field channel models, on the interference distribution caused by CEEs and model mismatches. Subsequently, by treating the interference as noise, we formulate a joint active and passive beamforming design problem to maximize the spectral efficiency (SE). The formulated problem is then recast as a mean squared error (MSE) minimization problem and a suboptimal algorithm is developed to iteratively update the active and passive beamforming strategies. Simulation results demonstrate that adopting the piece-wise near-field channel model leads to an improved SE compared to both the near-field and far-field models in the presence of CEEs. Furthermore, the proposed piece-wise near-field model achieves a good trade-off between modeling accuracy and system's degrees of freedom (DoF).

A Robust Super-resolution Gridless Imaging Framework for UAV-borne SAR Tomography

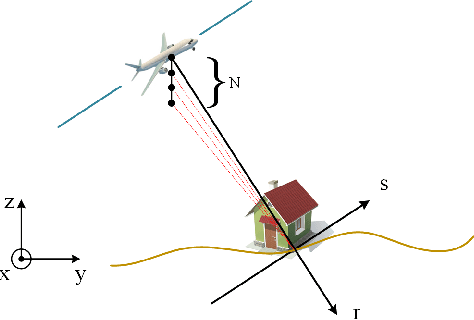
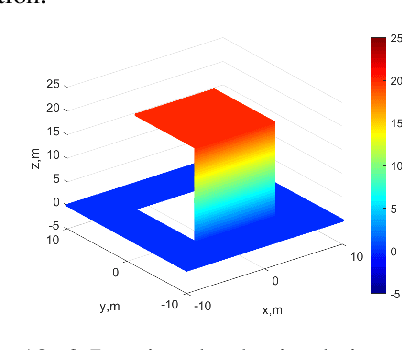
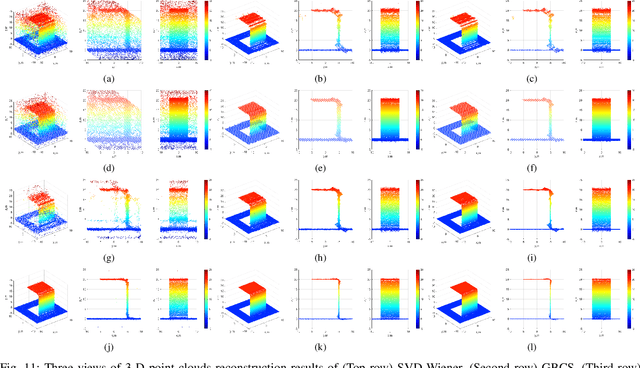
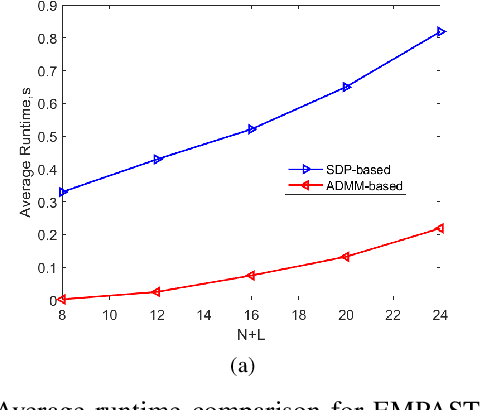
Synthetic aperture radar (SAR) tomography (TomoSAR) retrieves three-dimensional (3-D) information from multiple SAR images, effectively addresses the layover problem, and has become pivotal in urban mapping. Unmanned aerial vehicle (UAV) has gained popularity as a TomoSAR platform, offering distinct advantages such as the ability to achieve 3-D imaging in a single flight, cost-effectiveness, rapid deployment, and flexible trajectory planning. The evolution of compressed sensing (CS) has led to the widespread adoption of sparse reconstruction techniques in TomoSAR signal processing, with a focus on $\ell _1$ norm regularization and other grid-based CS methods. However, the discretization of illuminated scene along elevation introduces modeling errors, resulting in reduced reconstruction accuracy, known as the "off-grid" effect. Recent advancements have introduced gridless CS algorithms to mitigate this issue. This paper presents an innovative gridless 3-D imaging framework tailored for UAV-borne TomoSAR. Capitalizing on the pulse repetition frequency (PRF) redundancy inherent in slow UAV platforms, a multiple measurement vectors (MMV) model is constructed to enhance noise immunity without compromising azimuth-range resolution. Given the sparsely placed array elements due to mounting platform constraints, an atomic norm soft thresholding algorithm is proposed for partially observed MMV, offering gridless reconstruction capability and super-resolution. An efficient alternative optimization algorithm is also employed to enhance computational efficiency. Validation of the proposed framework is achieved through computer simulations and flight experiments, affirming its efficacy in UAV-borne TomoSAR applications.

Multichannel Frequency Estimation in Challenging Scenarios via Structured Matrix Embedding and Recovery (StruMER)

Multichannel frequency estimation with incomplete data and miscellaneous noises arises in array signal processing, modal analysis, wireless communications, and so on. In this paper, we consider maximum-likelihood(-like) optimization methods for frequency estimation in which proper objective functions are adopted subject to observed data patterns and noise types. We propose a universal signal-domain approach to solve the optimization problems by embedding the noiseless multichannel signal of interest into a series of low-rank positive-semidefinite block matrices of Hankel and Toeplitz submatrices and formulating the original parameter-domain optimization problems as equivalent structured matrix recovery problems. The alternating direction method of multipliers (ADMM) is applied to solve the resulting matrix recovery problems in which both subproblems of ADMM are solved in (nearly) closed form. The proposed approach is termed as structured matrix embedding and recovery (StruMER). Extensive numerical simulations are provided to demonstrate that StruMER has improved threshold performances in various challenging scenarios, e.g., limited data, low signal-to-noise ratio, impulsive noise, and closely spaced frequencies, as compared with state-of-the-art methods.

Direction-of-Arrival Estimation for Constant Modulus Signals Using a Structured Matrix Recovery Technique

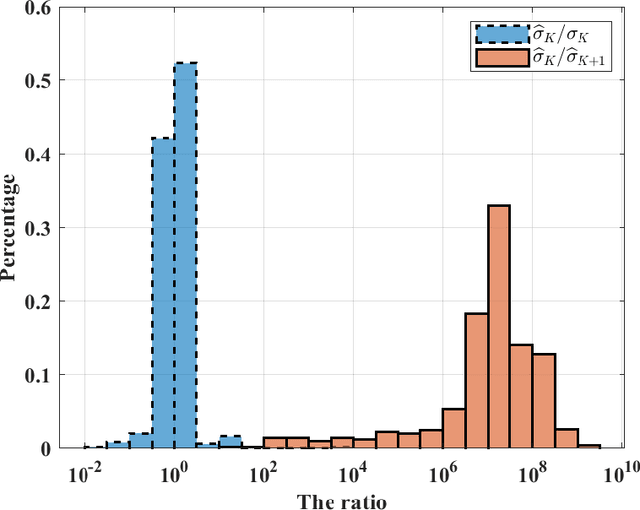
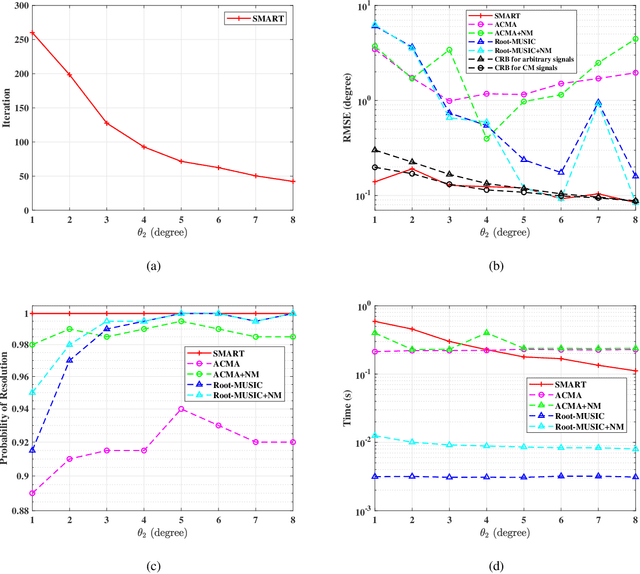
This paper addresses the problem of direction-of-arrival (DOA) estimation for constant modulus (CM) source signals using a uniform or sparse linear array. Existing methods typically exploit either the Vandermonde structure of the steering matrix or the CM structure of source signals only. In this paper, we propose a structured matrix recovery technique (SMART) for CM DOA estimation via fully exploiting the two structures. In particular, we reformulate the highly nonconvex CM DOA estimation problems in the noiseless and noisy cases as equivalent rank-constrained Hankel-Toeplitz matrix recovery problems, in which the Vandermonde structure is captured by a series of Hankel-Toeplitz block matrices, of which the number equals the number of snapshots, and the CM structure is guaranteed by letting the block matrices share a same Toeplitz submatrix. The alternating direction method of multipliers (ADMM) is applied to solve the resulting rank-constrained problems and the DOAs are uniquely retrieved from the numerical solution. Extensive simulations are carried out to corroborate our analysis and confirm that the proposed SMART outperforms state-of-the-art algorithms in terms of the maximum number of locatable sources and statistical efficiency.

Integrated Sensing, Navigation, and Communication for Secure UAV Networks with a Mobile Eavesdropper

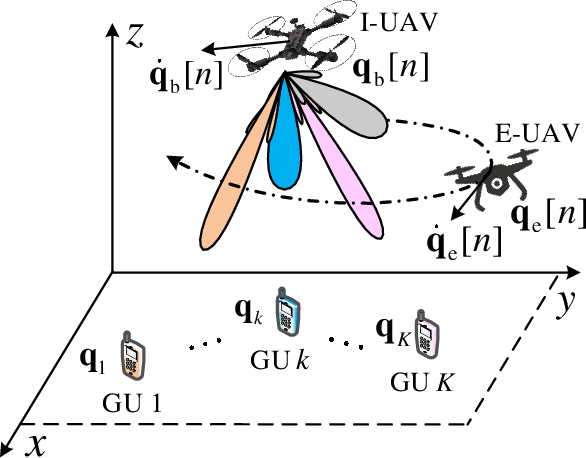
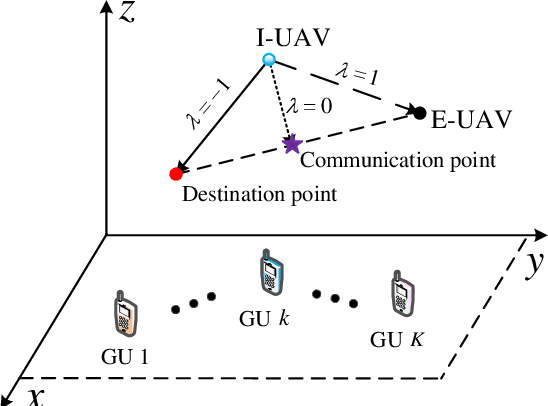
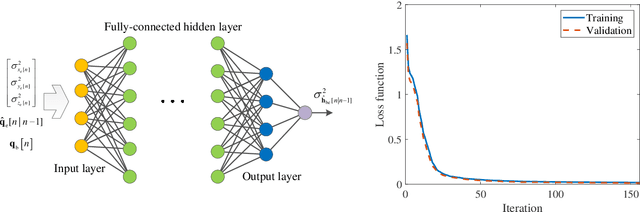
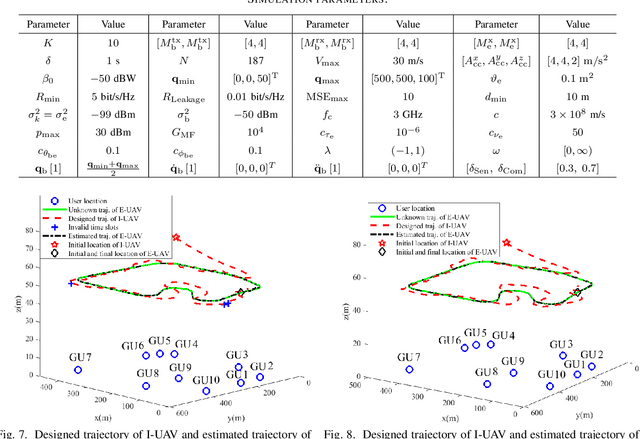
This paper proposes an integrated sensing, navigation, and communication (ISNC) framework for safeguarding unmanned aerial vehicle (UAV)-enabled wireless networks against a mobile eavesdropping UAV (E-UAV). To cope with the mobility of the E-UAV, the proposed framework advocates the dual use of artificial noise transmitted by the information UAV (I-UAV) for simultaneous jamming and sensing to facilitate navigation and secure communication. In particular, the I-UAV communicates with legitimate downlink ground users, while avoiding potential information leakage by emitting jamming signals, and estimates the state of the E-UAV with an extended Kalman filter based on the backscattered jamming signals. Exploiting the estimated state of the E-UAV in the previous time slot, the I-UAV determines its flight planning strategy, predicts the wiretap channel, and designs its communication resource allocation policy for the next time slot. To circumvent the severe coupling between these three tasks, a divide-and-conquer approach is adopted. The online navigation design has the objective to minimize the distance between the I-UAV and a pre-defined destination point considering kinematic and geometric constraints. Subsequently, given the predicted wiretap channel, the robust resource allocation design is formulated as an optimization problem to achieve the optimal trade-off between sensing and communication in the next time slot, while taking into account the wiretap channel prediction error and the quality-of-service (QoS) requirements of secure communication. Simulation results demonstrate the superior performance of the proposed design compared with baseline schemes and validate the benefits of integrating sensing and navigation into secure UAV communication systems.

Nonasymptotic Performance Analysis of Direct-Augmentation and Spatial-Smoothing ESPRIT for Localization of More Sources Than Sensors Using Sparse Arrays

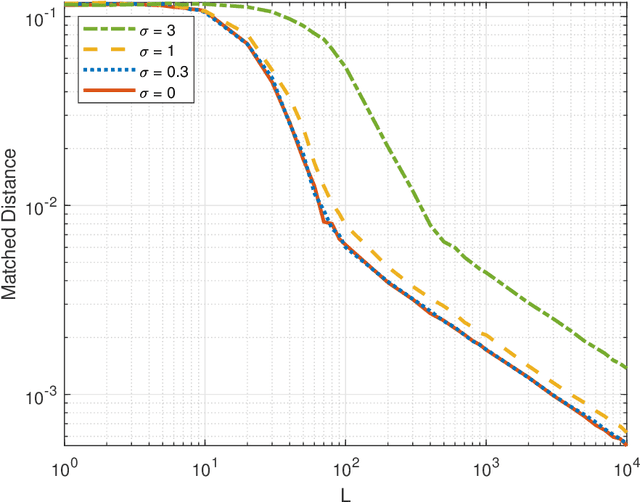
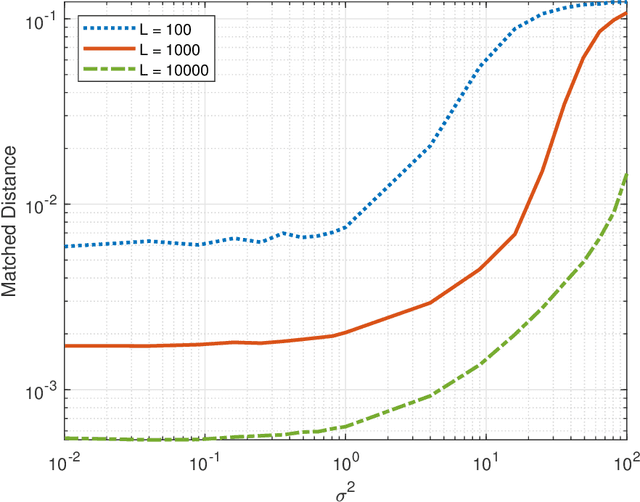
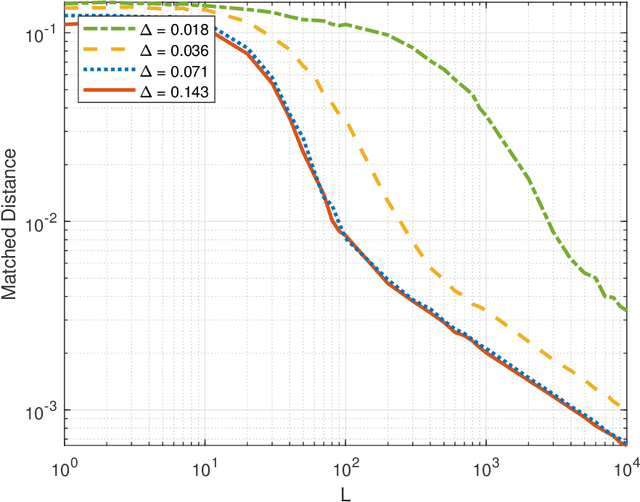
Direction augmentation (DA) and spatial smoothing (SS), followed by a subspace method such as ESPRIT or MUSIC, are two simple and successful approaches that enable localization of more uncorrelated sources than sensors with a proper sparse array. In this paper, we carry out nonasymptotic performance analyses of DA-ESPRIT and SS-ESPRIT in the practical finite-snapshot regime. We show that their absolute localization errors are bounded from above by $C_1\frac{\max\{\sigma^2, C_2\}}{\sqrt{L}}$ with overwhelming probability, where $L$ is the snapshot number, $\sigma^2$ is the Gaussian noise power, and $C_1,C_2$ are constants independent of $L$ and $\sigma^2$, if and only if they can do exact source localization with infinitely many snapshots. We also show that their resolution increases with the snapshot number, without a substantial limit. Numerical results corroborating our analysis are provided.

Separation-Free Spectral Super-Resolution via Convex Optimization

Atomic norm methods have recently been proposed for spectral super-resolution with flexibility in dealing with missing data and miscellaneous noises. A notorious drawback of these convex optimization methods however is their lower resolution in the high signal-to-noise (SNR) regime as compared to conventional methods such as ESPRIT. In this paper, we devise a simple weighting scheme in existing atomic norm methods and show that the resolution of the resulting convex optimization method can be made arbitrarily high in the absence of noise, achieving the so-called separation-free super-resolution. This is proved by a novel, kernel-free construction of the dual certificate whose existence guarantees exact super-resolution using the proposed method. Numerical results corroborating our analysis are provided.

A Robust and Statistically Efficient Maximum-Likelihood Method for DOA Estimation Using Sparse Linear Arrays

A recent trend of research on direction-of-arrival (DOA) estimation is to localize more uncorrelated sources than sensors by using a proper sparse linear array (SLA) and the Toeplitz covariance structure, at a cost of robustness to source correlations. In this paper, we make an attempt to achieve the two goals simultaneously by using a single algorithm. In order to statistically efficiently localize a maximal number of uncorrelated sources, we propose an effective algorithm for the stochastic maximum likelihood (SML) method based on elegant problem reformulations and the alternating direction method of multipliers (ADMM). We prove that the SML is robust to source correlations though it is derived under the assumption of uncorrelated sources. The proposed algorithm is usable for arbitrary SLAs (e.g., minimum redundancy arrays, nested arrays and coprime arrays) and is named as {\em m}aximum-likelihood {\em e}stimation via {\em s}equential {\em A}DMM (MESA). Extensive numerical results are provided that collaborate our analysis and demonstrate the statistical efficiency and robustness of MESA among state-of-the-art algorithms.