A Robust and Statistically Efficient Maximum-Likelihood Method for DOA Estimation Using Sparse Linear Arrays
Paper and Code
Mar 25, 2022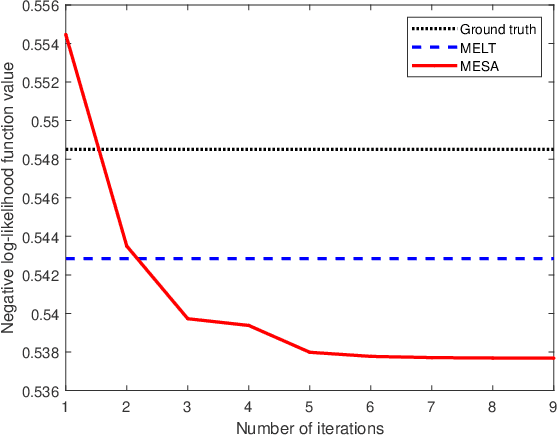

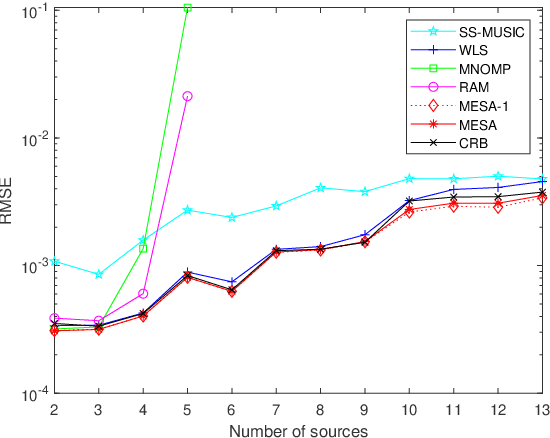

A recent trend of research on direction-of-arrival (DOA) estimation is to localize more uncorrelated sources than sensors by using a proper sparse linear array (SLA) and the Toeplitz covariance structure, at a cost of robustness to source correlations. In this paper, we make an attempt to achieve the two goals simultaneously by using a single algorithm. In order to statistically efficiently localize a maximal number of uncorrelated sources, we propose an effective algorithm for the stochastic maximum likelihood (SML) method based on elegant problem reformulations and the alternating direction method of multipliers (ADMM). We prove that the SML is robust to source correlations though it is derived under the assumption of uncorrelated sources. The proposed algorithm is usable for arbitrary SLAs (e.g., minimum redundancy arrays, nested arrays and coprime arrays) and is named as {\em m}aximum-likelihood {\em e}stimation via {\em s}equential {\em A}DMM (MESA). Extensive numerical results are provided that collaborate our analysis and demonstrate the statistical efficiency and robustness of MESA among state-of-the-art algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge