Direction-of-Arrival Estimation for Constant Modulus Signals Using a Structured Matrix Recovery Technique

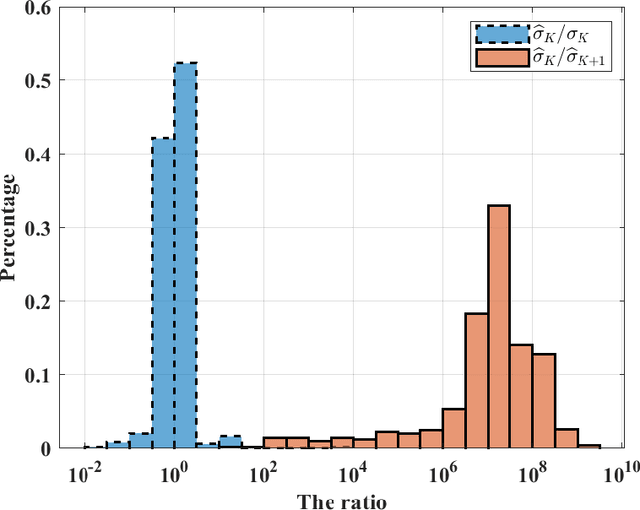
This paper addresses the problem of direction-of-arrival (DOA) estimation for constant modulus (CM) source signals using a uniform or sparse linear array. Existing methods typically exploit either the Vandermonde structure of the steering matrix or the CM structure of source signals only. In this paper, we propose a structured matrix recovery technique (SMART) for CM DOA estimation via fully exploiting the two structures. In particular, we reformulate the highly nonconvex CM DOA estimation problems in the noiseless and noisy cases as equivalent rank-constrained Hankel-Toeplitz matrix recovery problems, in which the Vandermonde structure is captured by a series of Hankel-Toeplitz block matrices, of which the number equals the number of snapshots, and the CM structure is guaranteed by letting the block matrices share a same Toeplitz submatrix. The alternating direction method of multipliers (ADMM) is applied to solve the resulting rank-constrained problems and the DOAs are uniquely retrieved from the numerical solution. Extensive simulations are carried out to corroborate our analysis and confirm that the proposed SMART outperforms state-of-the-art algorithms in terms of the maximum number of locatable sources and statistical efficiency.

Multichannel Frequency Estimation in Challenging Scenarios via Structured Matrix Embedding and Recovery (StruMER)

Multichannel frequency estimation with incomplete data and miscellaneous noises arises in array signal processing, modal analysis, wireless communications, and so on. In this paper, we consider maximum-likelihood(-like) optimization methods for frequency estimation in which proper objective functions are adopted subject to observed data patterns and noise types. We propose a universal signal-domain approach to solve the optimization problems by embedding the noiseless multichannel signal of interest into a series of low-rank positive-semidefinite block matrices of Hankel and Toeplitz submatrices and formulating the original parameter-domain optimization problems as equivalent structured matrix recovery problems. The alternating direction method of multipliers (ADMM) is applied to solve the resulting matrix recovery problems in which both subproblems of ADMM are solved in (nearly) closed form. The proposed approach is termed as structured matrix embedding and recovery (StruMER). Extensive numerical simulations are provided to demonstrate that StruMER has improved threshold performances in various challenging scenarios, e.g., limited data, low signal-to-noise ratio, impulsive noise, and closely spaced frequencies, as compared with state-of-the-art methods.

A Robust and Statistically Efficient Maximum-Likelihood Method for DOA Estimation Using Sparse Linear Arrays

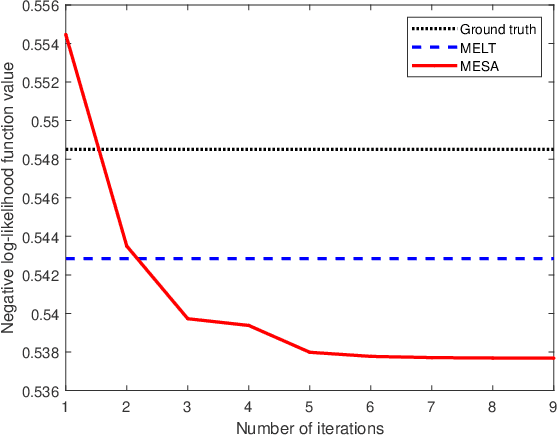
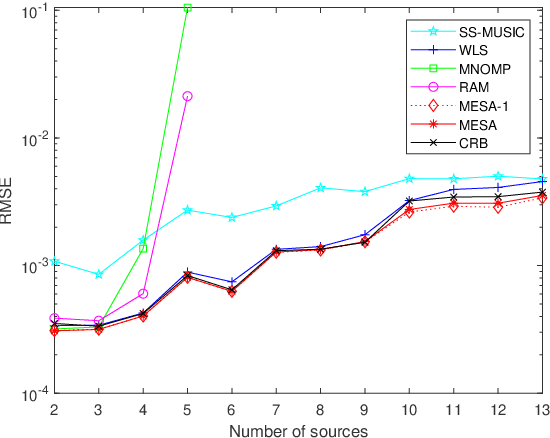
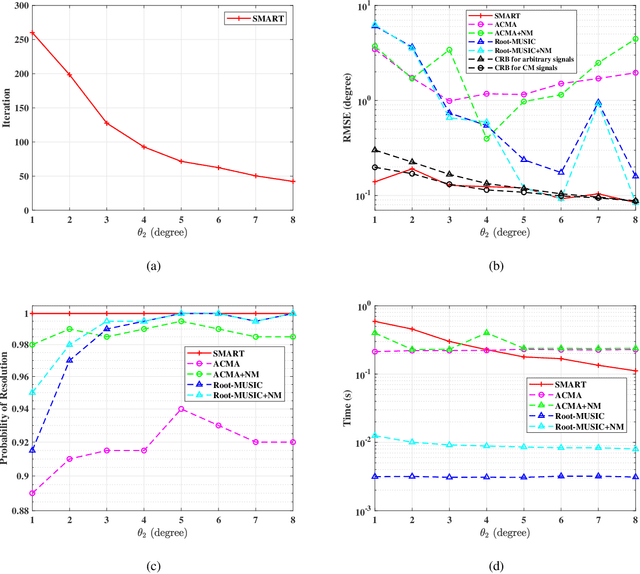
A recent trend of research on direction-of-arrival (DOA) estimation is to localize more uncorrelated sources than sensors by using a proper sparse linear array (SLA) and the Toeplitz covariance structure, at a cost of robustness to source correlations. In this paper, we make an attempt to achieve the two goals simultaneously by using a single algorithm. In order to statistically efficiently localize a maximal number of uncorrelated sources, we propose an effective algorithm for the stochastic maximum likelihood (SML) method based on elegant problem reformulations and the alternating direction method of multipliers (ADMM). We prove that the SML is robust to source correlations though it is derived under the assumption of uncorrelated sources. The proposed algorithm is usable for arbitrary SLAs (e.g., minimum redundancy arrays, nested arrays and coprime arrays) and is named as {\em m}aximum-likelihood {\em e}stimation via {\em s}equential {\em A}DMM (MESA). Extensive numerical results are provided that collaborate our analysis and demonstrate the statistical efficiency and robustness of MESA among state-of-the-art algorithms.

New Low Rank Optimization Model and Convex Approach for Robust Spectral Compressed Sensing

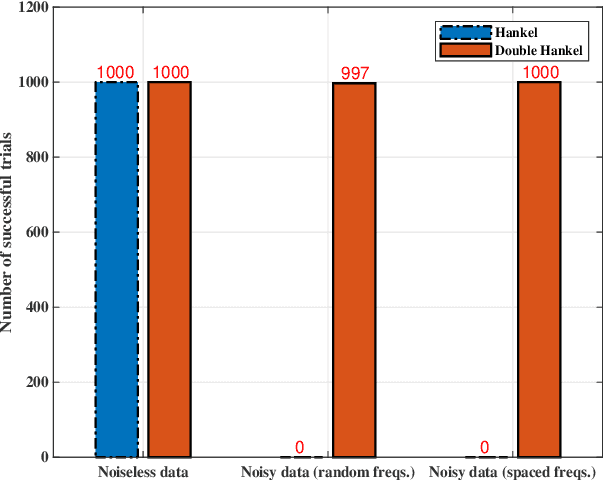
This paper investigates recovery of an undamped spectrally sparse signal and its spectral components from a set of regularly spaced samples within the framework of spectral compressed sensing and super-resolution. We show that the existing Hankel-based optimization methods suffer from the fundamental limitation that the prior of undampedness cannot be exploited. We propose a new low rank optimization model partially inspired by forward-backward processing for line spectral estimation and show its capability in restricting the spectral poles on the unit circle. We present convex relaxation approaches with the model and show their provable accuracy and robustness to bounded and sparse noise. All our results are generalized from the 1-D to arbitrary-dimensional spectral compressed sensing. Numerical simulations are provided that corroborate our analysis and show efficiency of our model and advantageous performance of our approach in improved accuracy and resolution as compared to the state-of-the-art Hankel and atomic norm methods.