New Low Rank Optimization Model and Convex Approach for Robust Spectral Compressed Sensing
Paper and Code
Jan 16, 2021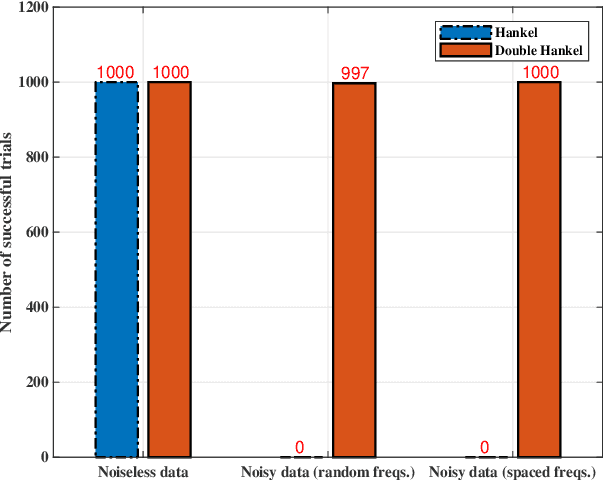



This paper investigates recovery of an undamped spectrally sparse signal and its spectral components from a set of regularly spaced samples within the framework of spectral compressed sensing and super-resolution. We show that the existing Hankel-based optimization methods suffer from the fundamental limitation that the prior of undampedness cannot be exploited. We propose a new low rank optimization model partially inspired by forward-backward processing for line spectral estimation and show its capability in restricting the spectral poles on the unit circle. We present convex relaxation approaches with the model and show their provable accuracy and robustness to bounded and sparse noise. All our results are generalized from the 1-D to arbitrary-dimensional spectral compressed sensing. Numerical simulations are provided that corroborate our analysis and show efficiency of our model and advantageous performance of our approach in improved accuracy and resolution as compared to the state-of-the-art Hankel and atomic norm methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge