Deep Kernel Learning via Random Fourier Features
Paper and Code
Oct 07, 2019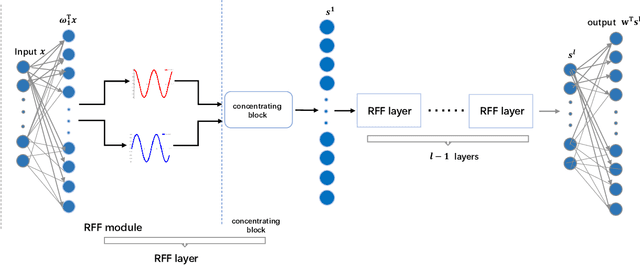
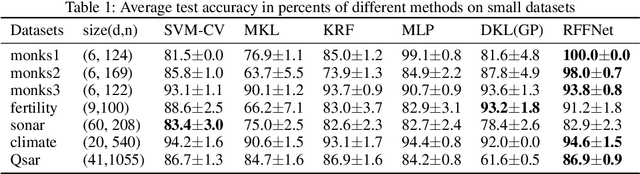
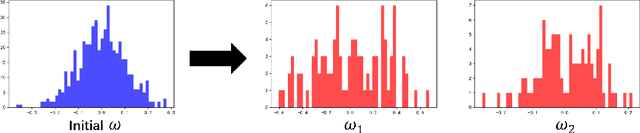
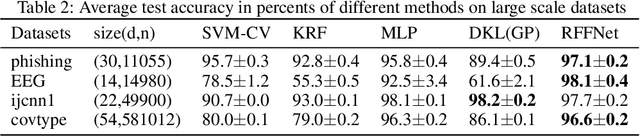
Kernel learning methods are among the most effective learning methods and have been vigorously studied in the past decades. However, when tackling with complicated tasks, classical kernel methods are not flexible or "rich" enough to describe the data and hence could not yield satisfactory performance. In this paper, via Random Fourier Features (RFF), we successfully incorporate the deep architecture into kernel learning, which significantly boosts the flexibility and richness of kernel machines while keeps kernels' advantage of pairwise handling small data. With RFF, we could establish a deep structure and make every kernel in RFF layers could be trained end-to-end. Since RFF with different distributions could represent different kernels, our model has the capability of finding suitable kernels for each layer, which is much more flexible than traditional kernel-based methods where the kernel is pre-selected. This fact also helps yield a more sophisticated kernel cascade connection in the architecture. On small datasets (less than 1000 samples), for which deep learning is generally not suitable due to overfitting, our method achieves superior performance compared to advanced kernel methods. On large-scale datasets, including non-image and image classification tasks, our method also has competitive performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge