FastAttention: Extend FlashAttention2 to NPUs and Low-resource GPUs

FlashAttention series has been widely applied in the inference of large language models (LLMs). However, FlashAttention series only supports the high-level GPU architectures, e.g., Ampere and Hopper. At present, FlashAttention series is not easily transferrable to NPUs and low-resource GPUs. Moreover, FlashAttention series is inefficient for multi- NPUs or GPUs inference scenarios. In this work, we propose FastAttention which pioneers the adaptation of FlashAttention series for NPUs and low-resource GPUs to boost LLM inference efficiency. Specifically, we take Ascend NPUs and Volta-based GPUs as representatives for designing our FastAttention. We migrate FlashAttention series to Ascend NPUs by proposing a novel two-level tiling strategy for runtime speedup, tiling-mask strategy for memory saving and the tiling-AllReduce strategy for reducing communication overhead, respectively. Besides, we adapt FlashAttention for Volta-based GPUs by redesigning the operands layout in shared memory and introducing a simple yet effective CPU-GPU cooperative strategy for efficient memory utilization. On Ascend NPUs, our FastAttention can achieve a 10.7$\times$ speedup compared to the standard attention implementation. Llama-7B within FastAttention reaches up to 5.16$\times$ higher throughput than within the standard attention. On Volta architecture GPUs, FastAttention yields 1.43$\times$ speedup compared to its equivalents in \texttt{xformers}. Pangu-38B within FastAttention brings 1.46$\times$ end-to-end speedup using FasterTransformer. Coupled with the propose CPU-GPU cooperative strategy, FastAttention supports a maximal input length of 256K on 8 V100 GPUs. All the codes will be made available soon.

FlatQuant: Flatness Matters for LLM Quantization

Recently, quantization has been widely used for the compression and acceleration of large language models~(LLMs). Due to the outliers in LLMs, it is crucial to flatten weights and activations to minimize quantization error with the equally spaced quantization points. Prior research explores various pre-quantization transformations to suppress outliers, such as per-channel scaling and Hadamard transformation. However, we observe that these transformed weights and activations can still remain steep and outspread. In this paper, we propose FlatQuant (Fast and Learnable Affine Transformation), a new post-training quantization approach to enhance flatness of weights and activations. Our approach identifies optimal affine transformations tailored to each linear layer, calibrated in hours via a lightweight objective. To reduce runtime overhead, we apply Kronecker decomposition to the transformation matrices, and fuse all operations in FlatQuant into a single kernel. Extensive experiments show that FlatQuant sets up a new state-of-the-art quantization benchmark. For instance, it achieves less than $\textbf{1}\%$ accuracy drop for W4A4 quantization on the LLaMA-3-70B model, surpassing SpinQuant by $\textbf{7.5}\%$. For inference latency, FlatQuant reduces the slowdown induced by pre-quantization transformation from 0.26x of QuaRot to merely $\textbf{0.07x}$, bringing up to $\textbf{2.3x}$ speedup for prefill and $\textbf{1.7x}$ speedup for decoding, respectively. Code is available at: \url{https://github.com/ruikangliu/FlatQuant}.

Multiway Spherical Clustering via Degree-Corrected Tensor Block Models

We consider the problem of multiway clustering in the presence of unknown degree heterogeneity. Such data problems arise commonly in applications such as recommendation system, neuroimaging, community detection, and hypergraph partitions in social networks. The allowance of degree heterogeneity provides great flexibility in clustering models, but the extra complexity poses significant challenges in both statistics and computation. Here, we develop a degree-corrected tensor block model with estimation accuracy guarantees. We present the phase transition of clustering performance based on the notion of angle separability, and we characterize three signal-to-noise regimes corresponding to different statistical-computational behaviors. In particular, we demonstrate that an intrinsic statistical-to-computational gap emerges only for tensors of order three or greater. Further, we develop an efficient polynomial-time algorithm that provably achieves exact clustering under mild signal conditions. The efficacy of our procedure is demonstrated through two data applications, one on human brain connectome project, and another on Peru Legislation network dataset.

Generalized tensor regression with covariates on multiple modes

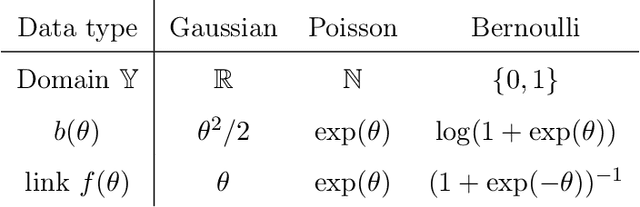
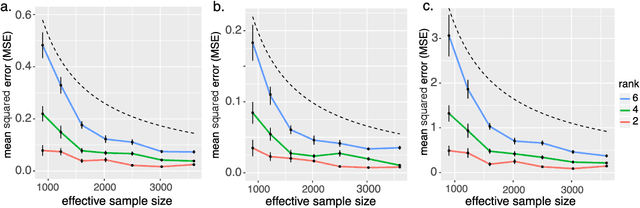
We consider the problem of tensor-response regression given covariates on multiple modes. Such data problems arise frequently in applications such as neuroimaging, network analysis, and spatial-temporal modeling. We propose a new family of tensor response regression models that incorporate covariates, and establish the theoretical accuracy guarantees. Unlike earlier methods, our estimation allows high-dimensionality in both the tensor response and the covariate matrices on multiple modes. An efficient alternating updating algorithm is further developed. Our proposal handles a broad range of data types, including continuous, count, and binary observations. Through simulation and applications to two real datasets, we demonstrate the outperformance of our approach over the state-of-art.