Do Large Language Models Have Compositional Ability? An Investigation into Limitations and Scalability

Large language models (LLMs) have emerged as powerful tools for many AI problems and exhibit remarkable in-context learning (ICL) capabilities. Compositional ability, solving unseen complex tasks that combine two or more simple tasks, is an essential reasoning ability for Artificial General Intelligence. Despite LLM's tremendous success, how they approach composite tasks, especially those not encountered during the pretraining phase, remains an open question and largely ununderstood. In this study, we delve into the ICL capabilities of LLMs on composite tasks, with only simple tasks as in-context examples. We develop a test suite of composite tasks that include linguistic and logical challenges and perform empirical studies across different LLM families. We observe that models exhibit divergent behaviors: (1) For simpler composite tasks that apply distinct mapping mechanisms to different input segments, the models demonstrate decent compositional ability, while scaling up the model enhances this ability; (2) for more complex composite tasks that involving reasoning multiple steps, where each step represent one task, models typically underperform, and scaling up generally provide no improvements. We offer theoretical analysis in a simplified setting, explaining that models exhibit compositional capability when the task handles different input parts separately. We believe our work sheds new light on the capabilities of LLMs in solving composite tasks regarding the nature of the tasks and model scale. Our dataset and code are available at {\url{https://github.com/OliverXUZY/LLM_Compose}}.

Why Larger Language Models Do In-context Learning Differently?

Large language models (LLM) have emerged as a powerful tool for AI, with the key ability of in-context learning (ICL), where they can perform well on unseen tasks based on a brief series of task examples without necessitating any adjustments to the model parameters. One recent interesting mysterious observation is that models of different scales may have different ICL behaviors: larger models tend to be more sensitive to noise in the test context. This work studies this observation theoretically aiming to improve the understanding of LLM and ICL. We analyze two stylized settings: (1) linear regression with one-layer single-head linear transformers and (2) parity classification with two-layer multiple attention heads transformers (non-linear data and non-linear model). In both settings, we give closed-form optimal solutions and find that smaller models emphasize important hidden features while larger ones cover more hidden features; thus, smaller models are more robust to noise while larger ones are more easily distracted, leading to different ICL behaviors. This sheds light on where transformers pay attention to and how that affects ICL. Preliminary experimental results on large base and chat models provide positive support for our analysis.

Towards Few-Shot Adaptation of Foundation Models via Multitask Finetuning

Foundation models have emerged as a powerful tool for many AI problems. Despite the tremendous success of foundation models, effective adaptation to new tasks, particularly those with limited labels, remains an open question and lacks theoretical understanding. An emerging solution with recent success in vision and NLP involves finetuning a foundation model on a selection of relevant tasks, before its adaptation to a target task with limited labeled samples. In this paper, we study the theoretical justification of this multitask finetuning approach. Our theoretical analysis reveals that with a diverse set of related tasks, this multitask finetuning leads to reduced error in the target task, in comparison to directly adapting the same pretrained model. We quantify the relationship between finetuning tasks and target tasks by diversity and consistency metrics, and further propose a practical task selection algorithm. We substantiate our theoretical claims with extensive empirical evidence. Further, we present results affirming our task selection algorithm adeptly chooses related finetuning tasks, providing advantages to the model performance on target tasks. We believe our study shed new light on the effective adaptation of foundation models to new tasks that lack abundant labels. Our code is available at https://github.com/OliverXUZY/Foudation-Model_Multitask.

Spatial Transcriptomics Dimensionality Reduction using Wavelet Bases

Spatially resolved transcriptomics (ST) measures gene expression along with the spatial coordinates of the measurements. The analysis of ST data involves significant computation complexity. In this work, we propose gene expression dimensionality reduction algorithm that retains spatial structure. We combine the wavelet transformation with matrix factorization to select spatially-varying genes. We extract a low-dimensional representation of these genes. We consider Empirical Bayes setting, imposing regularization through the prior distribution of factor genes. Additionally, We provide visualization of extracted representation genes capturing the global spatial pattern. We illustrate the performance of our methods by spatial structure recovery and gene expression reconstruction in simulation. In real data experiments, our method identifies spatial structure of gene factors and outperforms regular decomposition regarding reconstruction error. We found the connection between the fluctuation of gene patterns and wavelet technique, providing smoother visualization. We develop the package and share the workflow generating reproducible quantitative results and gene visualization. The package is available at https://github.com/OliverXUZY/waveST.

Generalized tensor regression with covariates on multiple modes

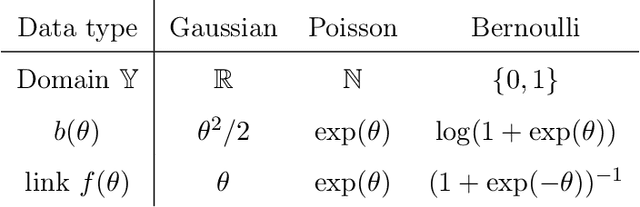
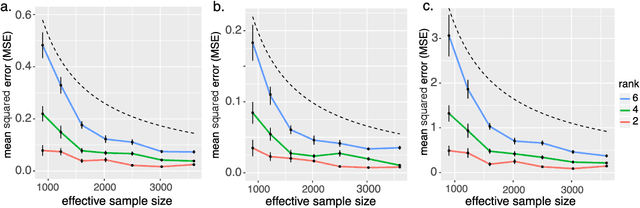
We consider the problem of tensor-response regression given covariates on multiple modes. Such data problems arise frequently in applications such as neuroimaging, network analysis, and spatial-temporal modeling. We propose a new family of tensor response regression models that incorporate covariates, and establish the theoretical accuracy guarantees. Unlike earlier methods, our estimation allows high-dimensionality in both the tensor response and the covariate matrices on multiple modes. An efficient alternating updating algorithm is further developed. Our proposal handles a broad range of data types, including continuous, count, and binary observations. Through simulation and applications to two real datasets, we demonstrate the outperformance of our approach over the state-of-art.