Generalized tensor regression with covariates on multiple modes

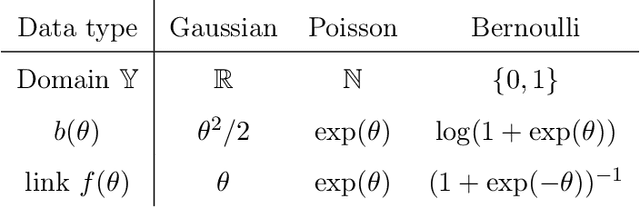
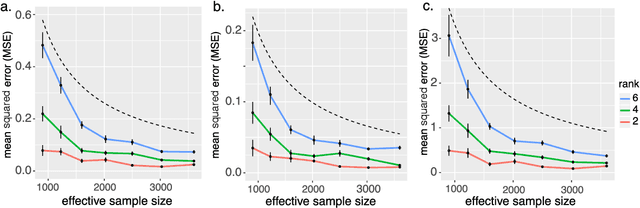
We consider the problem of tensor-response regression given covariates on multiple modes. Such data problems arise frequently in applications such as neuroimaging, network analysis, and spatial-temporal modeling. We propose a new family of tensor response regression models that incorporate covariates, and establish the theoretical accuracy guarantees. Unlike earlier methods, our estimation allows high-dimensionality in both the tensor response and the covariate matrices on multiple modes. An efficient alternating updating algorithm is further developed. Our proposal handles a broad range of data types, including continuous, count, and binary observations. Through simulation and applications to two real datasets, we demonstrate the outperformance of our approach over the state-of-art.