Statistical and computational rates in high rank tensor estimation

Higher-order tensor datasets arise commonly in recommendation systems, neuroimaging, and social networks. Here we develop probable methods for estimating a possibly high rank signal tensor from noisy observations. We consider a generative latent variable tensor model that incorporates both high rank and low rank models, including but not limited to, simple hypergraphon models, single index models, low-rank CP models, and low-rank Tucker models. Comprehensive results are developed on both the statistical and computational limits for the signal tensor estimation. We find that high-dimensional latent variable tensors are of log-rank; the fact explains the pervasiveness of low-rank tensors in applications. Furthermore, we propose a polynomial-time spectral algorithm that achieves the computationally optimal rate. We show that the statistical-computational gap emerges only for latent variable tensors of order 3 or higher. Numerical experiments and two real data applications are presented to demonstrate the practical merits of our methods.

Multiway Spherical Clustering via Degree-Corrected Tensor Block Models

We consider the problem of multiway clustering in the presence of unknown degree heterogeneity. Such data problems arise commonly in applications such as recommendation system, neuroimaging, community detection, and hypergraph partitions in social networks. The allowance of degree heterogeneity provides great flexibility in clustering models, but the extra complexity poses significant challenges in both statistics and computation. Here, we develop a degree-corrected tensor block model with estimation accuracy guarantees. We present the phase transition of clustering performance based on the notion of angle separability, and we characterize three signal-to-noise regimes corresponding to different statistical-computational behaviors. In particular, we demonstrate that an intrinsic statistical-to-computational gap emerges only for tensors of order three or greater. Further, we develop an efficient polynomial-time algorithm that provably achieves exact clustering under mild signal conditions. The efficacy of our procedure is demonstrated through two data applications, one on human brain connectome project, and another on Peru Legislation network dataset.

Smooth tensor estimation with unknown permutations

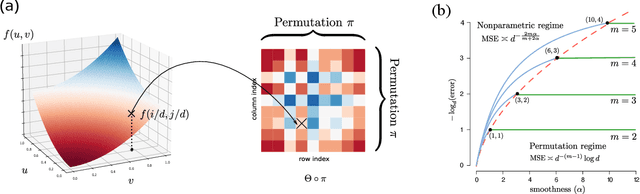
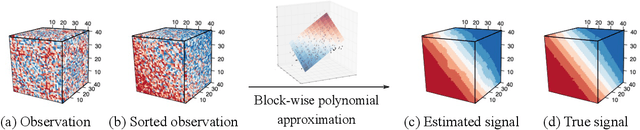
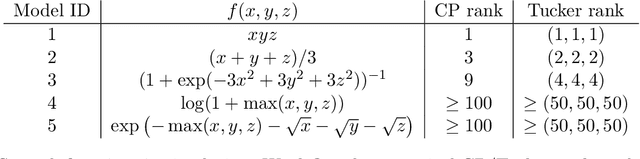
We consider the problem of structured tensor denoising in the presence of unknown permutations. Such data problems arise commonly in recommendation system, neuroimaging, community detection, and multiway comparison applications. Here, we develop a general family of smooth tensor models up to arbitrary index permutations; the model incorporates the popular tensor block models and Lipschitz hypergraphon models as special cases. We show that a constrained least-squares estimator in the block-wise polynomial family achieves the minimax error bound. A phase transition phenomenon is revealed with respect to the smoothness threshold needed for optimal recovery. In particular, we find that a polynomial of degree up to $(m-2)(m+1)/2$ is sufficient for accurate recovery of order-$m$ tensors, whereas higher degree exhibits no further benefits. This phenomenon reveals the intrinsic distinction for smooth tensor estimation problems with and without unknown permutations. Furthermore, we provide an efficient polynomial-time Borda count algorithm that provably achieves optimal rate under monotonicity assumptions. The efficacy of our procedure is demonstrated through both simulations and Chicago crime data analysis.

Nonparametric Trace Regression in High Dimensions via Sign Series Representation

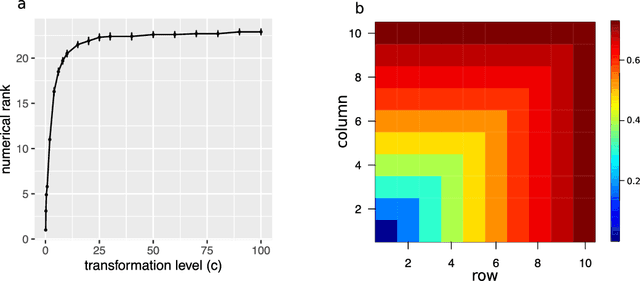
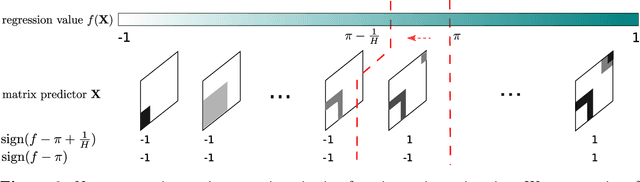
Learning of matrix-valued data has recently surged in a range of scientific and business applications. Trace regression is a widely used method to model effects of matrix predictors and has shown great success in matrix learning. However, nearly all existing trace regression solutions rely on two assumptions: (i) a known functional form of the conditional mean, and (ii) a global low-rank structure in the entire range of the regression function, both of which may be violated in practice. In this article, we relax these assumptions by developing a general framework for nonparametric trace regression models via structured sign series representations of high dimensional functions. The new model embraces both linear and nonlinear trace effects, and enjoys rank invariance to order-preserving transformations of the response. In the context of matrix completion, our framework leads to a substantially richer model based on what we coin as the "sign rank" of a matrix. We show that the sign series can be statistically characterized by weighted classification tasks. Based on this connection, we propose a learning reduction approach to learn the regression model via a series of classifiers, and develop a parallelable computation algorithm to implement sign series aggregations. We establish the excess risk bounds, estimation error rates, and sample complexities. Our proposal provides a broad nonparametric paradigm to many important matrix learning problems, including matrix regression, matrix completion, multi-task learning, and compressed sensing. We demonstrate the advantages of our method through simulations and two applications, one on brain connectivity study and the other on high-rank image completion.

Beyond the Signs: Nonparametric Tensor Completion via Sign Series

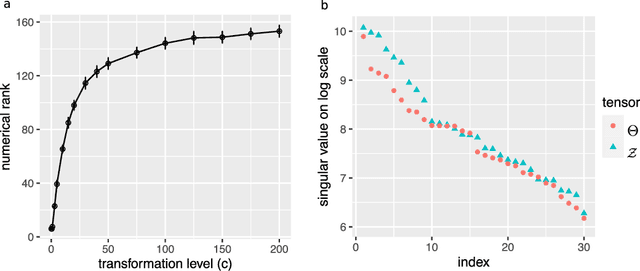
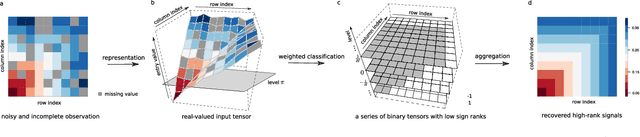
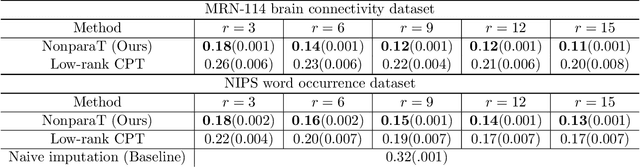
We consider the problem of tensor estimation from noisy observations with possibly missing entries. A nonparametric approach to tensor completion is developed based on a new model which we coin as sign representable tensors. The model represents the signal tensor of interest using a series of structured sign tensors. Unlike earlier methods, the sign series representation effectively addresses both low- and high-rank signals, while encompassing many existing tensor models -- including CP models, Tucker models, single index models, several hypergraphon models -- as special cases. We show that the sign tensor series is theoretically characterized, and computationally estimable, via classification tasks with carefully-specified weights. Excess risk bounds, estimation error rates, and sample complexities are established. We demonstrate the outperformance of our approach over previous methods on two datasets, one on human brain connectivity networks and the other on topic data mining.

Exact Clustering in Tensor Block Model: Statistical Optimality and Computational Limit

High-order clustering aims to identify heterogeneous substructure in multiway dataset that arises commonly in neuroimaging, genomics, and social network studies. The non-convex and discontinuous nature of the problem poses significant challenges in both statistics and computation. In this paper, we propose a tensor block model and the computationally efficient methods, \emph{high-order Lloyd algorithm} (HLloyd) and \emph{high-order spectral clustering} (HSC), for high-order clustering in tensor block model. The convergence of the proposed procedure is established, and we show that our method achieves exact clustering under reasonable assumptions. We also give the complete characterization for the statistical-computational trade-off in high-order clustering based on three different signal-to-noise ratio regimes. Finally, we show the merits of the proposed procedures via extensive experiments on both synthetic and real datasets.

Tensor denoising and completion based on ordinal observations

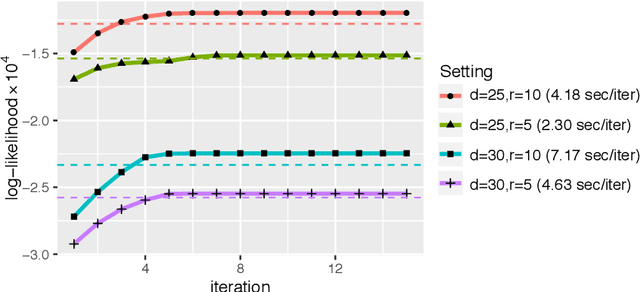
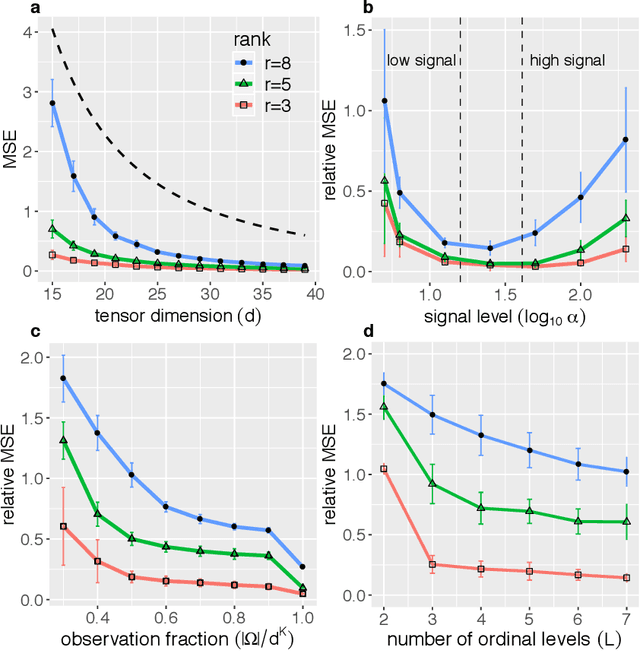
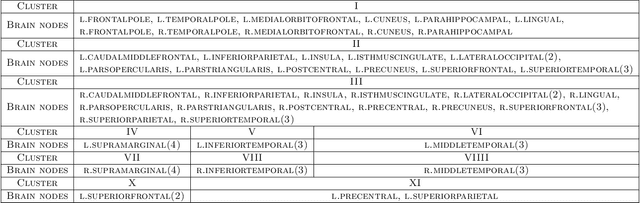
Higher-order tensors arise frequently in applications such as neuroimaging, recommendation system, social network analysis, and psychological studies. We consider the problem of low-rank tensor estimation from possibly incomplete, ordinal-valued observations. Two related problems are studied, one on tensor denoising and another on tensor completion. We propose a multi-linear cumulative link model, develop a rank-constrained M-estimator, and obtain theoretical accuracy guarantees. Our mean squared error bound enjoys a faster convergence rate than previous results, and we show that the proposed estimator is minimax optimal under the class of low-rank models. Furthermore, the procedure developed serves as an efficient completion method which guarantees consistent recovery of an order-$K$ $(d,\ldots,d)$-dimensional low-rank tensor using only $\tilde{\mathcal{O}}(Kd)$ noisy, quantized observations. We demonstrate the outperformance of our approach over previous methods on the tasks of clustering and collaborative filtering.

Generalized tensor regression with covariates on multiple modes

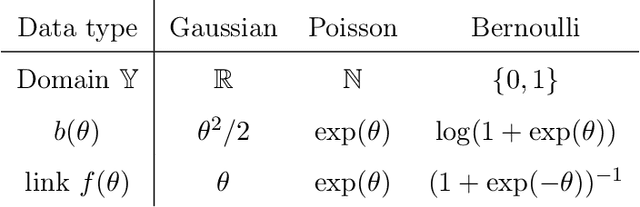
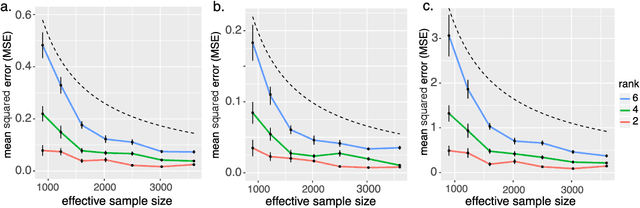
We consider the problem of tensor-response regression given covariates on multiple modes. Such data problems arise frequently in applications such as neuroimaging, network analysis, and spatial-temporal modeling. We propose a new family of tensor response regression models that incorporate covariates, and establish the theoretical accuracy guarantees. Unlike earlier methods, our estimation allows high-dimensionality in both the tensor response and the covariate matrices on multiple modes. An efficient alternating updating algorithm is further developed. Our proposal handles a broad range of data types, including continuous, count, and binary observations. Through simulation and applications to two real datasets, we demonstrate the outperformance of our approach over the state-of-art.

Multiway clustering via tensor block models

We consider the problem of identifying multiway block structure from a large noisy tensor. Such problems arise frequently in applications such as genomics, recommendation system, topic modeling, and sensor network localization. We propose a tensor block model, develop a unified least-square estimation, and obtain the theoretical accuracy guarantees for multiway clustering. The statistical convergence of the estimator is established, and we show that the associated clustering procedure achieves partition consistency. A sparse regularization is further developed for identifying important blocks with elevated means. The proposal handles a broad range of data types, including binary, continuous, and hybrid observations. Through simulation and application to two real datasets, we demonstrate the outperformance of our approach over previous methods.

Learning from Binary Multiway Data: Probabilistic Tensor Decomposition and its Statistical Optimality

We consider the problem of decomposition of multiway tensor with binary entries. Such data problems arise frequently in numerous applications such as neuroimaging, recommendation system, topic modeling, and sensor network localization. We propose that the observed binary entries follow a Bernoulli model, develop a rank-constrained likelihood-based estimation procedure, and obtain the theoretical accuracy guarantees. Specifically, we establish the error bound of the tensor estimation, and show that the obtained rate is minimax optimal under the considered model. We demonstrate the efficacy of our approach through both simulations and analyses of multiple real-world datasets on the tasks of tensor completion and clustering.