Semi-pessimistic Reinforcement Learning

Offline reinforcement learning (RL) aims to learn an optimal policy from pre-collected data. However, it faces challenges of distributional shift, where the learned policy may encounter unseen scenarios not covered in the offline data. Additionally, numerous applications suffer from a scarcity of labeled reward data. Relying on labeled data alone often leads to a narrow state-action distribution, further amplifying the distributional shift, and resulting in suboptimal policy learning. To address these issues, we first recognize that the volume of unlabeled data is typically substantially larger than that of labeled data. We then propose a semi-pessimistic RL method to effectively leverage abundant unlabeled data. Our approach offers several advantages. It considerably simplifies the learning process, as it seeks a lower bound of the reward function, rather than that of the Q-function or state transition function. It is highly flexible, and can be integrated with a range of model-free and model-based RL algorithms. It enjoys the guaranteed improvement when utilizing vast unlabeled data, but requires much less restrictive conditions. We compare our method with a number of alternative solutions, both analytically and numerically, and demonstrate its clear competitiveness. We further illustrate with an application to adaptive deep brain stimulation for Parkinson's disease.

Incentivizing Truthful Language Models via Peer Elicitation Games

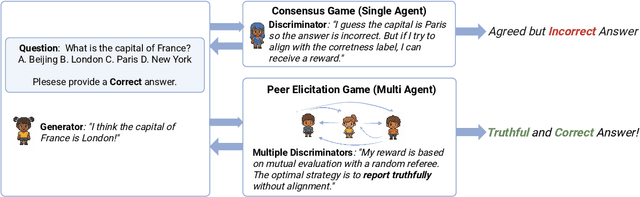
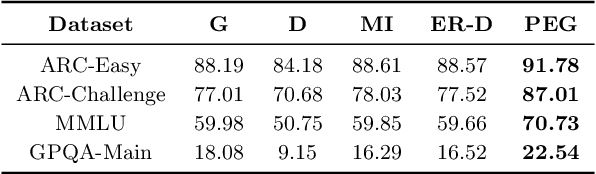
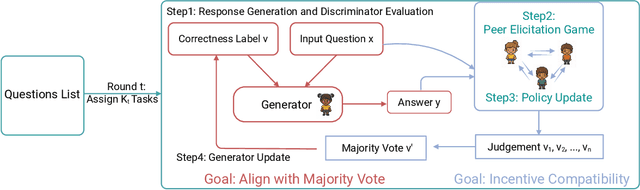
Large Language Models (LLMs) have demonstrated strong generative capabilities but remain prone to inconsistencies and hallucinations. We introduce Peer Elicitation Games (PEG), a training-free, game-theoretic framework for aligning LLMs through a peer elicitation mechanism involving a generator and multiple discriminators instantiated from distinct base models. Discriminators interact in a peer evaluation setting, where rewards are computed using a determinant-based mutual information score that provably incentivizes truthful reporting without requiring ground-truth labels. We establish theoretical guarantees showing that each agent, via online learning, achieves sublinear regret in the sense their cumulative performance approaches that of the best fixed truthful strategy in hindsight. Moreover, we prove last-iterate convergence to a truthful Nash equilibrium, ensuring that the actual policies used by agents converge to stable and truthful behavior over time. Empirical evaluations across multiple benchmarks demonstrate significant improvements in factual accuracy. These results position PEG as a practical approach for eliciting truthful behavior from LLMs without supervision or fine-tuning.

Residual Feature Integration is Sufficient to Prevent Negative Transfer

Transfer learning typically leverages representations learned from a source domain to improve performance on a target task. A common approach is to extract features from a pre-trained model and directly apply them for target prediction. However, this strategy is prone to negative transfer where the source representation fails to align with the target distribution. In this article, we propose Residual Feature Integration (REFINE), a simple yet effective method designed to mitigate negative transfer. Our approach combines a fixed source-side representation with a trainable target-side encoder and fits a shallow neural network on the resulting joint representation, which adapts to the target domain while preserving transferable knowledge from the source domain. Theoretically, we prove that REFINE is sufficient to prevent negative transfer under mild conditions, and derive the generalization bound demonstrating its theoretical benefit. Empirically, we show that REFINE consistently enhances performance across diverse application and data modalities including vision, text, and tabular data, and outperforms numerous alternative solutions. Our method is lightweight, architecture-agnostic, and robust, making it a valuable addition to the existing transfer learning toolbox.

Fairness-aware organ exchange and kidney paired donation

The kidney paired donation (KPD) program provides an innovative solution to overcome incompatibility challenges in kidney transplants by matching incompatible donor-patient pairs and facilitating kidney exchanges. To address unequal access to transplant opportunities, there are two widely used fairness criteria: group fairness and individual fairness. However, these criteria do not consider protected patient features, which refer to characteristics legally or ethically recognized as needing protection from discrimination, such as race and gender. Motivated by the calibration principle in machine learning, we introduce a new fairness criterion: the matching outcome should be conditionally independent of the protected feature, given the sensitization level. We integrate this fairness criterion as a constraint within the KPD optimization framework and propose a computationally efficient solution. Theoretically, we analyze the associated price of fairness using random graph models. Empirically, we compare our fairness criterion with group fairness and individual fairness through both simulations and a real-data example.

A Statistical Hypothesis Testing Framework for Data Misappropriation Detection in Large Language Models

Large Language Models (LLMs) are rapidly gaining enormous popularity in recent years. However, the training of LLMs has raised significant privacy and legal concerns, particularly regarding the inclusion of copyrighted materials in their training data without proper attribution or licensing, which falls under the broader issue of data misappropriation. In this article, we focus on a specific problem of data misappropriation detection, namely, to determine whether a given LLM has incorporated data generated by another LLM. To address this issue, we propose embedding watermarks into the copyrighted training data and formulating the detection of data misappropriation as a hypothesis testing problem. We develop a general statistical testing framework, construct a pivotal statistic, determine the optimal rejection threshold, and explicitly control the type I and type II errors. Furthermore, we establish the asymptotic optimality properties of the proposed tests, and demonstrate its empirical effectiveness through intensive numerical experiments.

Conformal Diffusion Models for Individual Treatment Effect Estimation and Inference

Estimating treatment effects from observational data is of central interest across numerous application domains. Individual treatment effect offers the most granular measure of treatment effect on an individual level, and is the most useful to facilitate personalized care. However, its estimation and inference remain underdeveloped due to several challenges. In this article, we propose a novel conformal diffusion model-based approach that addresses those intricate challenges. We integrate the highly flexible diffusion modeling, the model-free statistical inference paradigm of conformal inference, along with propensity score and covariate local approximation that tackle distributional shifts. We unbiasedly estimate the distributions of potential outcomes for individual treatment effect, construct an informative confidence interval, and establish rigorous theoretical guarantees. We demonstrate the competitive performance of the proposed method over existing solutions through extensive numerical studies.

Synthetic Oversampling: Theory and A Practical Approach Using LLMs to Address Data Imbalance

Imbalanced data and spurious correlations are common challenges in machine learning and data science. Oversampling, which artificially increases the number of instances in the underrepresented classes, has been widely adopted to tackle these challenges. In this article, we introduce OPAL (\textbf{O}versam\textbf{P}ling with \textbf{A}rtificial \textbf{L}LM-generated data), a systematic oversampling approach that leverages the capabilities of large language models (LLMs) to generate high-quality synthetic data for minority groups. Recent studies on synthetic data generation using deep generative models mostly target prediction tasks. Our proposal differs in that we focus on handling imbalanced data and spurious correlations. More importantly, we develop a novel theory that rigorously characterizes the benefits of using the synthetic data, and shows the capacity of transformers in generating high-quality synthetic data for both labels and covariates. We further conduct intensive numerical experiments to demonstrate the efficacy of our proposed approach compared to some representative alternative solutions.

Testing for the Markov Property in Time Series via Deep Conditional Generative Learning

The Markov property is widely imposed in analysis of time series data. Correspondingly, testing the Markov property, and relatedly, inferring the order of a Markov model, are of paramount importance. In this article, we propose a nonparametric test for the Markov property in high-dimensional time series via deep conditional generative learning. We also apply the test sequentially to determine the order of the Markov model. We show that the test controls the type-I error asymptotically, and has the power approaching one. Our proposal makes novel contributions in several ways. We utilize and extend state-of-the-art deep generative learning to estimate the conditional density functions, and establish a sharp upper bound on the approximation error of the estimators. We derive a doubly robust test statistic, which employs a nonparametric estimation but achieves a parametric convergence rate. We further adopt sample splitting and cross-fitting to minimize the conditions required to ensure the consistency of the test. We demonstrate the efficacy of the test through both simulations and the three data applications.

Sequential Best-Arm Identification with Application to Brain-Computer Interface

A brain-computer interface (BCI) is a technology that enables direct communication between the brain and an external device or computer system. It allows individuals to interact with the device using only their thoughts, and holds immense potential for a wide range of applications in medicine, rehabilitation, and human augmentation. An electroencephalogram (EEG) and event-related potential (ERP)-based speller system is a type of BCI that allows users to spell words without using a physical keyboard, but instead by recording and interpreting brain signals under different stimulus presentation paradigms. Conventional non-adaptive paradigms treat each word selection independently, leading to a lengthy learning process. To improve the sampling efficiency, we cast the problem as a sequence of best-arm identification tasks in multi-armed bandits. Leveraging pre-trained large language models (LLMs), we utilize the prior knowledge learned from previous tasks to inform and facilitate subsequent tasks. To do so in a coherent way, we propose a sequential top-two Thompson sampling (STTS) algorithm under the fixed-confidence setting and the fixed-budget setting. We study the theoretical property of the proposed algorithm, and demonstrate its substantial empirical improvement through both synthetic data analysis as well as a P300 BCI speller simulator example.

Optimizing Pessimism in Dynamic Treatment Regimes: A Bayesian Learning Approach

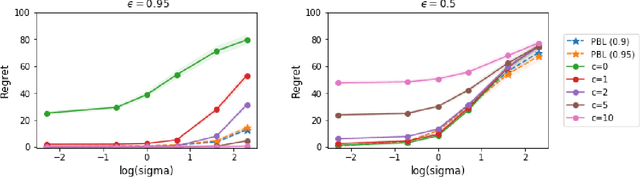
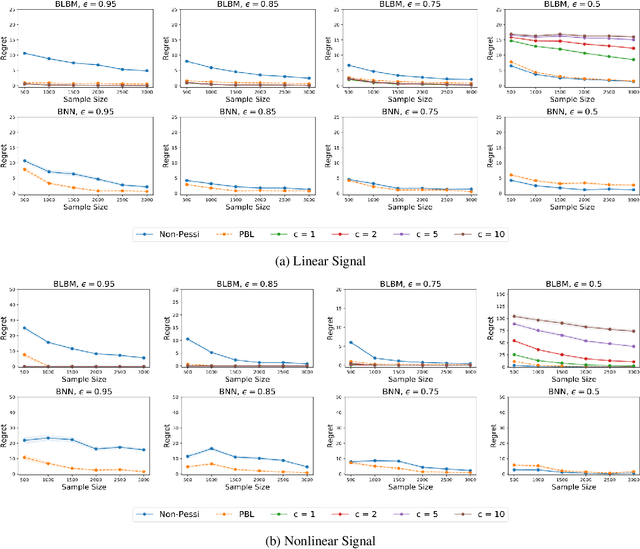
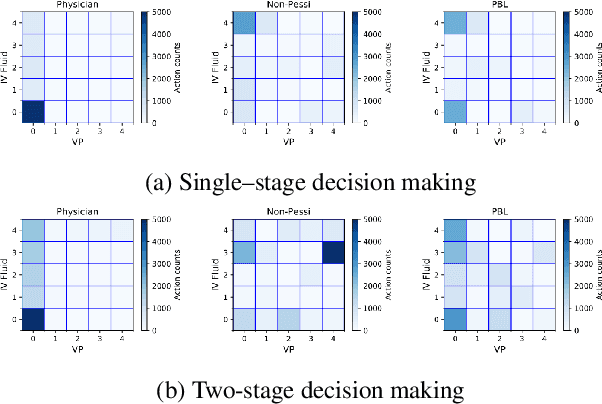
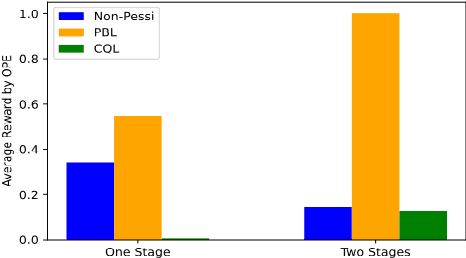
In this article, we propose a novel pessimism-based Bayesian learning method for optimal dynamic treatment regimes in the offline setting. When the coverage condition does not hold, which is common for offline data, the existing solutions would produce sub-optimal policies. The pessimism principle addresses this issue by discouraging recommendation of actions that are less explored conditioning on the state. However, nearly all pessimism-based methods rely on a key hyper-parameter that quantifies the degree of pessimism, and the performance of the methods can be highly sensitive to the choice of this parameter. We propose to integrate the pessimism principle with Thompson sampling and Bayesian machine learning for optimizing the degree of pessimism. We derive a credible set whose boundary uniformly lower bounds the optimal Q-function, and thus does not require additional tuning of the degree of pessimism. We develop a general Bayesian learning method that works with a range of models, from Bayesian linear basis model to Bayesian neural network model. We develop the computational algorithm based on variational inference, which is highly efficient and scalable. We establish the theoretical guarantees of the proposed method, and show empirically that it outperforms the existing state-of-the-art solutions through both simulations and a real data example.