Residual Feature Integration is Sufficient to Prevent Negative Transfer

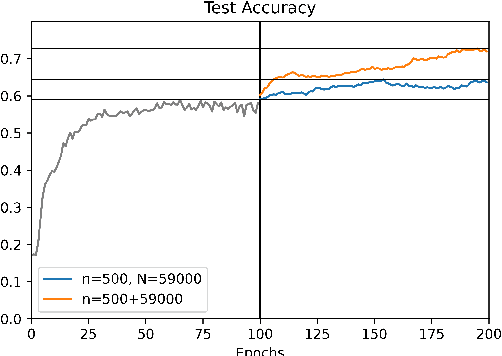
Transfer learning typically leverages representations learned from a source domain to improve performance on a target task. A common approach is to extract features from a pre-trained model and directly apply them for target prediction. However, this strategy is prone to negative transfer where the source representation fails to align with the target distribution. In this article, we propose Residual Feature Integration (REFINE), a simple yet effective method designed to mitigate negative transfer. Our approach combines a fixed source-side representation with a trainable target-side encoder and fits a shallow neural network on the resulting joint representation, which adapts to the target domain while preserving transferable knowledge from the source domain. Theoretically, we prove that REFINE is sufficient to prevent negative transfer under mild conditions, and derive the generalization bound demonstrating its theoretical benefit. Empirically, we show that REFINE consistently enhances performance across diverse application and data modalities including vision, text, and tabular data, and outperforms numerous alternative solutions. Our method is lightweight, architecture-agnostic, and robust, making it a valuable addition to the existing transfer learning toolbox.

A Theoretical Framework for Prompt Engineering: Approximating Smooth Functions with Transformer Prompts

Prompt engineering has emerged as a powerful technique for guiding large language models (LLMs) toward desired responses, significantly enhancing their performance across diverse tasks. Beyond their role as static predictors, LLMs increasingly function as intelligent agents, capable of reasoning, decision-making, and adapting dynamically to complex environments. However, the theoretical underpinnings of prompt engineering remain largely unexplored. In this paper, we introduce a formal framework demonstrating that transformer models, when provided with carefully designed prompts, can act as a configurable computational system by emulating a ``virtual'' neural network during inference. Specifically, input prompts effectively translate into the corresponding network configuration, enabling LLMs to adjust their internal computations dynamically. Building on this construction, we establish an approximation theory for $\beta$-times differentiable functions, proving that transformers can approximate such functions with arbitrary precision when guided by appropriately structured prompts. Moreover, our framework provides theoretical justification for several empirically successful prompt engineering techniques, including the use of longer, structured prompts, filtering irrelevant information, enhancing prompt token diversity, and leveraging multi-agent interactions. By framing LLMs as adaptable agents rather than static models, our findings underscore their potential for autonomous reasoning and problem-solving, paving the way for more robust and theoretically grounded advancements in prompt engineering and AI agent design.

S$^{2}$FT: Efficient, Scalable and Generalizable LLM Fine-tuning by Structured Sparsity

Current PEFT methods for LLMs can achieve either high quality, efficient training, or scalable serving, but not all three simultaneously. To address this limitation, we investigate sparse fine-tuning and observe a remarkable improvement in generalization ability. Utilizing this key insight, we propose a family of Structured Sparse Fine-Tuning (S$^{2}$FT) methods for LLMs, which concurrently achieve state-of-the-art fine-tuning performance, training efficiency, and inference scalability. S$^{2}$FT accomplishes this by "selecting sparsely and computing densely". It selects a few heads and channels in the MHA and FFN modules for each Transformer block, respectively. Next, it co-permutes weight matrices on both sides of the coupled structures in LLMs to connect the selected components in each layer into a dense submatrix. Finally, S$^{2}$FT performs in-place gradient updates on all submatrices. Through theoretical analysis and empirical results, our method prevents overfitting and forgetting, delivers SOTA performance on both commonsense and arithmetic reasoning with 4.6% and 1.3% average improvements compared to LoRA, and surpasses full FT by 11.5% when generalizing to various domains after instruction tuning. Using our partial backpropagation algorithm, S$^{2}$FT saves training memory up to 3$\times$ and improves latency by 1.5-2.7$\times$ compared to full FT, while delivering an average 10% improvement over LoRA on both metrics. We further demonstrate that the weight updates in S$^{2}$FT can be decoupled into adapters, enabling effective fusion, fast switch, and efficient parallelism for serving multiple fine-tuned models.

NEAT: Nonlinear Parameter-efficient Adaptation of Pre-trained Models

Fine-tuning pre-trained models is crucial for adapting large models to downstream tasks, often delivering state-of-the-art performance. However, fine-tuning all model parameters is resource-intensive and laborious, leading to the emergence of parameter-efficient fine-tuning (PEFT) methods. One widely adopted PEFT technique, Low-Rank Adaptation (LoRA), freezes the pre-trained model weights and introduces two low-rank matrices whose ranks are significantly smaller than the dimensions of the original weight matrices. This enables efficient fine-tuning by adjusting only a small number of parameters. Despite its efficiency, LoRA approximates weight updates using low-rank decomposition, which struggles to capture complex, non-linear components and efficient optimization trajectories. As a result, LoRA-based methods often exhibit a significant performance gap compared to full fine-tuning. Closing this gap requires higher ranks, which increases the number of parameters. To address these limitations, we propose a nonlinear parameter-efficient adaptation method (NEAT). NEAT introduces a lightweight neural network that takes pre-trained weights as input and learns a nonlinear transformation to approximate cumulative weight updates. These updates can be interpreted as functions of the corresponding pre-trained weights. The nonlinear approximation directly models the cumulative updates, effectively capturing complex and non-linear structures in the weight updates. Our theoretical analysis demonstrates taht NEAT can be more efficient than LoRA while having equal or greater expressivity. Extensive evaluations across four benchmarks and over twenty datasets demonstrate that NEAT significantly outperforms baselines in both vision and text tasks.

Synthetic Oversampling: Theory and A Practical Approach Using LLMs to Address Data Imbalance

Imbalanced data and spurious correlations are common challenges in machine learning and data science. Oversampling, which artificially increases the number of instances in the underrepresented classes, has been widely adopted to tackle these challenges. In this article, we introduce OPAL (\textbf{O}versam\textbf{P}ling with \textbf{A}rtificial \textbf{L}LM-generated data), a systematic oversampling approach that leverages the capabilities of large language models (LLMs) to generate high-quality synthetic data for minority groups. Recent studies on synthetic data generation using deep generative models mostly target prediction tasks. Our proposal differs in that we focus on handling imbalanced data and spurious correlations. More importantly, we develop a novel theory that rigorously characterizes the benefits of using the synthetic data, and shows the capacity of transformers in generating high-quality synthetic data for both labels and covariates. We further conduct intensive numerical experiments to demonstrate the efficacy of our proposed approach compared to some representative alternative solutions.

Contrastive Learning on Multimodal Analysis of Electronic Health Records

Electronic health record (EHR) systems contain a wealth of multimodal clinical data including structured data like clinical codes and unstructured data such as clinical notes. However, many existing EHR-focused studies has traditionally either concentrated on an individual modality or merged different modalities in a rather rudimentary fashion. This approach often results in the perception of structured and unstructured data as separate entities, neglecting the inherent synergy between them. Specifically, the two important modalities contain clinically relevant, inextricably linked and complementary health information. A more complete picture of a patient's medical history is captured by the joint analysis of the two modalities of data. Despite the great success of multimodal contrastive learning on vision-language, its potential remains under-explored in the realm of multimodal EHR, particularly in terms of its theoretical understanding. To accommodate the statistical analysis of multimodal EHR data, in this paper, we propose a novel multimodal feature embedding generative model and design a multimodal contrastive loss to obtain the multimodal EHR feature representation. Our theoretical analysis demonstrates the effectiveness of multimodal learning compared to single-modality learning and connects the solution of the loss function to the singular value decomposition of a pointwise mutual information matrix. This connection paves the way for a privacy-preserving algorithm tailored for multimodal EHR feature representation learning. Simulation studies show that the proposed algorithm performs well under a variety of configurations. We further validate the clinical utility of the proposed algorithm in real-world EHR data.

Safeguarding Data in Multimodal AI: A Differentially Private Approach to CLIP Training

The surge in multimodal AI's success has sparked concerns over data privacy in vision-and-language tasks. While CLIP has revolutionized multimodal learning through joint training on images and text, its potential to unintentionally disclose sensitive information necessitates the integration of privacy-preserving mechanisms. We introduce a differentially private adaptation of the Contrastive Language-Image Pretraining (CLIP) model that effectively addresses privacy concerns while retaining accuracy. Our proposed method, Dp-CLIP, is rigorously evaluated on benchmark datasets encompassing diverse vision-and-language tasks such as image classification and visual question answering. We demonstrate that our approach retains performance on par with the standard non-private CLIP model. Furthermore, we analyze our proposed algorithm under linear representation settings. We derive the convergence rate of our algorithm and show a trade-off between utility and privacy when gradients are clipped per-batch and the loss function does not satisfy smoothness conditions assumed in the literature for the analysis of DP-SGD.

Understanding Multimodal Contrastive Learning and Incorporating Unpaired Data

Language-supervised vision models have recently attracted great attention in computer vision. A common approach to build such models is to use contrastive learning on paired data across the two modalities, as exemplified by Contrastive Language-Image Pre-Training (CLIP). In this paper, under linear representation settings, (i) we initiate the investigation of a general class of nonlinear loss functions for multimodal contrastive learning (MMCL) including CLIP loss and show its connection to singular value decomposition (SVD). Namely, we show that each step of loss minimization by gradient descent can be seen as performing SVD on a contrastive cross-covariance matrix. Based on this insight, (ii) we analyze the performance of MMCL. We quantitatively show that the feature learning ability of MMCL can be better than that of unimodal contrastive learning applied to each modality even under the presence of wrongly matched pairs. This characterizes the robustness of MMCL to noisy data. Furthermore, when we have access to additional unpaired data, (iii) we propose a new MMCL loss that incorporates additional unpaired datasets. We show that the algorithm can detect the ground-truth pairs and improve performance by fully exploiting unpaired datasets. The performance of the proposed algorithm was verified by numerical experiments.

The Power of Contrast for Feature Learning: A Theoretical Analysis

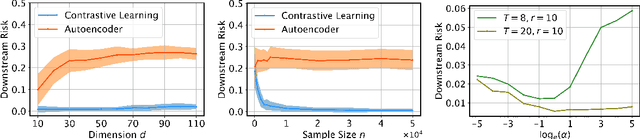
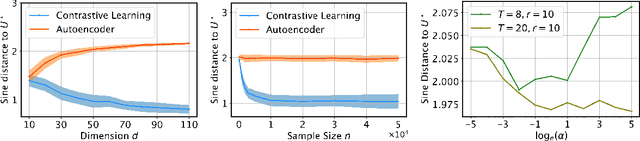
Contrastive learning has achieved state-of-the-art performance in various self-supervised learning tasks and even outperforms its supervised counterpart. Despite its empirical success, theoretical understanding of why contrastive learning works is still limited. In this paper, (i) we provably show that contrastive learning outperforms autoencoder, a classical unsupervised learning method, for both feature recovery and downstream tasks; (ii) we also illustrate the role of labeled data in supervised contrastive learning. This provides theoretical support for recent findings that contrastive learning with labels improves the performance of learned representations in the in-domain downstream task, but it can harm the performance in transfer learning. We verify our theory with numerical experiments.

Asymptotic Risk of Overparameterized Likelihood Models: Double Descent Theory for Deep Neural Networks

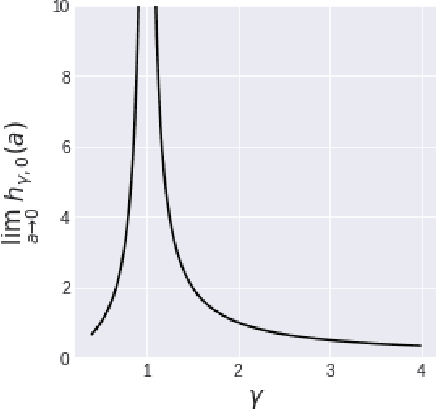
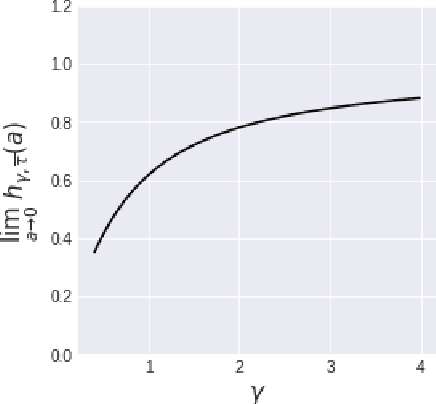
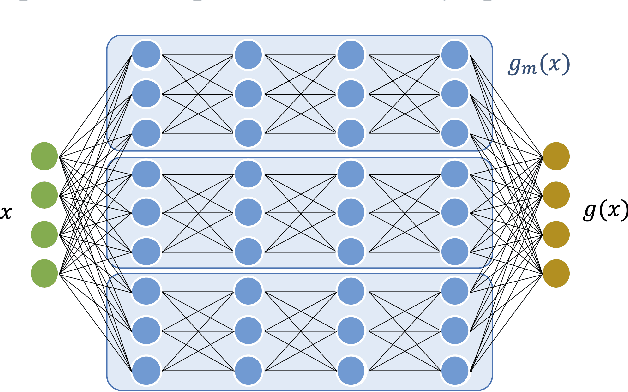
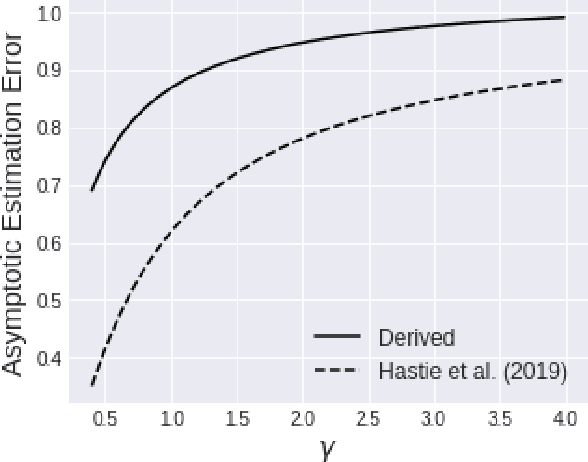
We investigate the asymptotic risk of a general class of overparameterized likelihood models, including deep models. The recent empirical success of large-scale models has motivated several theoretical studies to investigate a scenario wherein both the number of samples, $n$, and parameters, $p$, diverge to infinity and derive an asymptotic risk at the limit. However, these theorems are only valid for linear-in-feature models, such as generalized linear regression, kernel regression, and shallow neural networks. Hence, it is difficult to investigate a wider class of nonlinear models, including deep neural networks with three or more layers. In this study, we consider a likelihood maximization problem without the model constraints and analyze the upper bound of an asymptotic risk of an estimator with penalization. Technically, we combine a property of the Fisher information matrix with an extended Marchenko-Pastur law and associate the combination with empirical process techniques. The derived bound is general, as it describes both the double descent and the regularized risk curves, depending on the penalization. Our results are valid without the linear-in-feature constraints on models and allow us to derive the general spectral distributions of a Fisher information matrix from the likelihood. We demonstrate that several explicit models, such as parallel deep neural networks, ensemble learning, and residual networks, are in agreement with our theory. This result indicates that even large and deep models have a small asymptotic risk if they exhibit a specific structure, such as divisibility. To verify this finding, we conduct a real-data experiment with parallel deep neural networks. Our results expand the applicability of the asymptotic risk analysis, and may also contribute to the understanding and application of deep learning.