Asymptotic Risk of Overparameterized Likelihood Models: Double Descent Theory for Deep Neural Networks
Paper and Code
Mar 15, 2021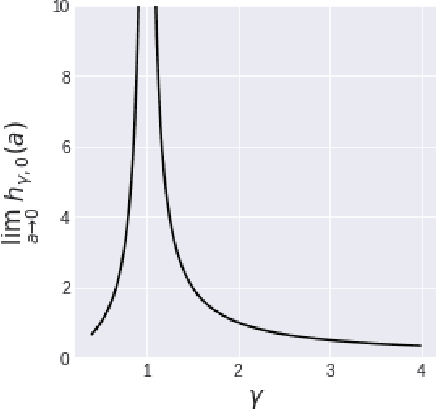
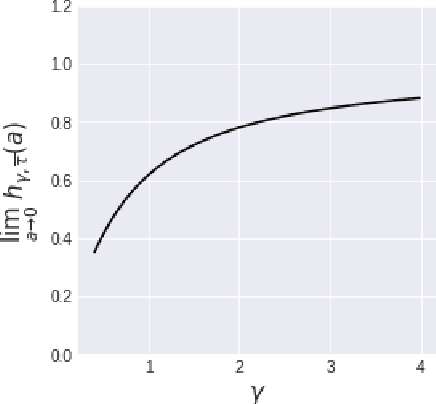
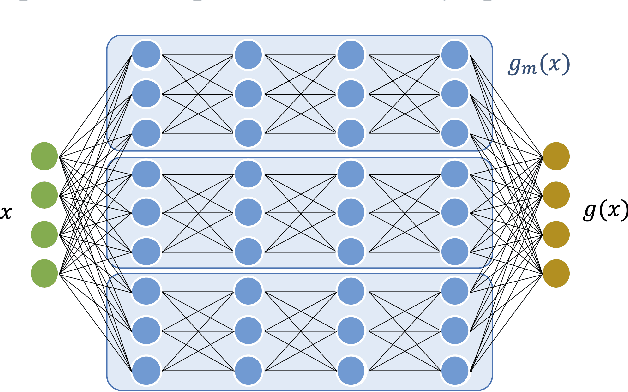
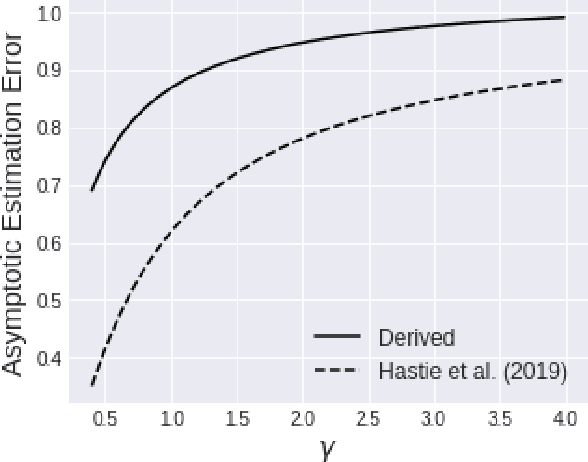
We investigate the asymptotic risk of a general class of overparameterized likelihood models, including deep models. The recent empirical success of large-scale models has motivated several theoretical studies to investigate a scenario wherein both the number of samples, $n$, and parameters, $p$, diverge to infinity and derive an asymptotic risk at the limit. However, these theorems are only valid for linear-in-feature models, such as generalized linear regression, kernel regression, and shallow neural networks. Hence, it is difficult to investigate a wider class of nonlinear models, including deep neural networks with three or more layers. In this study, we consider a likelihood maximization problem without the model constraints and analyze the upper bound of an asymptotic risk of an estimator with penalization. Technically, we combine a property of the Fisher information matrix with an extended Marchenko-Pastur law and associate the combination with empirical process techniques. The derived bound is general, as it describes both the double descent and the regularized risk curves, depending on the penalization. Our results are valid without the linear-in-feature constraints on models and allow us to derive the general spectral distributions of a Fisher information matrix from the likelihood. We demonstrate that several explicit models, such as parallel deep neural networks, ensemble learning, and residual networks, are in agreement with our theory. This result indicates that even large and deep models have a small asymptotic risk if they exhibit a specific structure, such as divisibility. To verify this finding, we conduct a real-data experiment with parallel deep neural networks. Our results expand the applicability of the asymptotic risk analysis, and may also contribute to the understanding and application of deep learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge