Globally Optimal Training of Neural Networks with Threshold Activation Functions

Threshold activation functions are highly preferable in neural networks due to their efficiency in hardware implementations. Moreover, their mode of operation is more interpretable and resembles that of biological neurons. However, traditional gradient based algorithms such as Gradient Descent cannot be used to train the parameters of neural networks with threshold activations since the activation function has zero gradient except at a single non-differentiable point. To this end, we study weight decay regularized training problems of deep neural networks with threshold activations. We first show that regularized deep threshold network training problems can be equivalently formulated as a standard convex optimization problem, which parallels the LASSO method, provided that the last hidden layer width exceeds a certain threshold. We also derive a simplified convex optimization formulation when the dataset can be shattered at a certain layer of the network. We corroborate our theoretical results with various numerical experiments.

Understanding Multimodal Contrastive Learning and Incorporating Unpaired Data

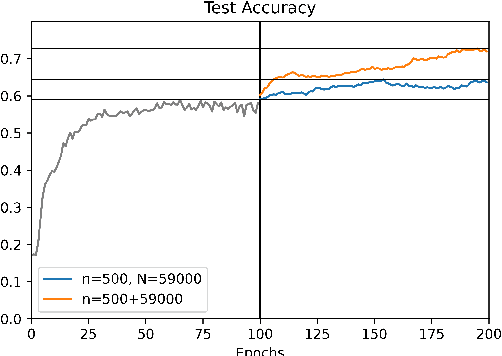
Language-supervised vision models have recently attracted great attention in computer vision. A common approach to build such models is to use contrastive learning on paired data across the two modalities, as exemplified by Contrastive Language-Image Pre-Training (CLIP). In this paper, under linear representation settings, (i) we initiate the investigation of a general class of nonlinear loss functions for multimodal contrastive learning (MMCL) including CLIP loss and show its connection to singular value decomposition (SVD). Namely, we show that each step of loss minimization by gradient descent can be seen as performing SVD on a contrastive cross-covariance matrix. Based on this insight, (ii) we analyze the performance of MMCL. We quantitatively show that the feature learning ability of MMCL can be better than that of unimodal contrastive learning applied to each modality even under the presence of wrongly matched pairs. This characterizes the robustness of MMCL to noisy data. Furthermore, when we have access to additional unpaired data, (iii) we propose a new MMCL loss that incorporates additional unpaired datasets. We show that the algorithm can detect the ground-truth pairs and improve performance by fully exploiting unpaired datasets. The performance of the proposed algorithm was verified by numerical experiments.

Towards Sample-efficient Overparameterized Meta-learning

An overarching goal in machine learning is to build a generalizable model with few samples. To this end, overparameterization has been the subject of immense interest to explain the generalization ability of deep nets even when the size of the dataset is smaller than that of the model. While the prior literature focuses on the classical supervised setting, this paper aims to demystify overparameterization for meta-learning. Here we have a sequence of linear-regression tasks and we ask: (1) Given earlier tasks, what is the optimal linear representation of features for a new downstream task? and (2) How many samples do we need to build this representation? This work shows that surprisingly, overparameterization arises as a natural answer to these fundamental meta-learning questions. Specifically, for (1), we first show that learning the optimal representation coincides with the problem of designing a task-aware regularization to promote inductive bias. We leverage this inductive bias to explain how the downstream task actually benefits from overparameterization, in contrast to prior works on few-shot learning. For (2), we develop a theory to explain how feature covariance can implicitly help reduce the sample complexity well below the degrees of freedom and lead to small estimation error. We then integrate these findings to obtain an overall performance guarantee for our meta-learning algorithm. Numerical experiments on real and synthetic data verify our insights on overparameterized meta-learning.

Sample Efficient Subspace-based Representations for Nonlinear Meta-Learning

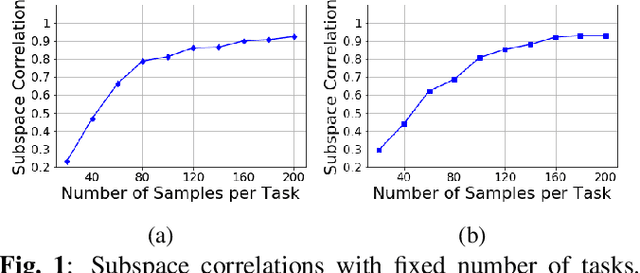
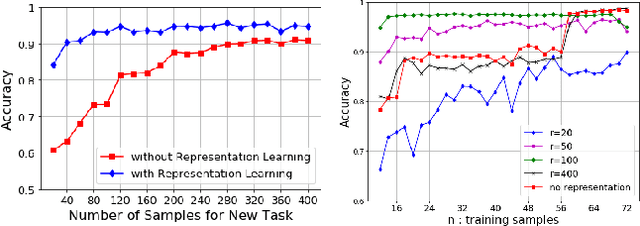
Constructing good representations is critical for learning complex tasks in a sample efficient manner. In the context of meta-learning, representations can be constructed from common patterns of previously seen tasks so that a future task can be learned quickly. While recent works show the benefit of subspace-based representations, such results are limited to linear-regression tasks. This work explores a more general class of nonlinear tasks with applications ranging from binary classification, generalized linear models and neural nets. We prove that subspace-based representations can be learned in a sample-efficient manner and provably benefit future tasks in terms of sample complexity. Numerical results verify the theoretical predictions in classification and neural-network regression tasks.