Global Convergence of Four-Layer Matrix Factorization under Random Initialization

Gradient descent dynamics on the deep matrix factorization problem is extensively studied as a simplified theoretical model for deep neural networks. Although the convergence theory for two-layer matrix factorization is well-established, no global convergence guarantee for general deep matrix factorization under random initialization has been established to date. To address this gap, we provide a polynomial-time global convergence guarantee for randomly initialized gradient descent on four-layer matrix factorization, given certain conditions on the target matrix and a standard balanced regularization term. Our analysis employs new techniques to show saddle-avoidance properties of gradient decent dynamics, and extends previous theories to characterize the change in eigenvalues of layer weights.

Global Convergence of Gradient EM for Over-Parameterized Gaussian Mixtures

Learning Gaussian Mixture Models (GMMs) is a fundamental problem in machine learning, with the Expectation-Maximization (EM) algorithm and its popular variant gradient EM being arguably the most widely used algorithms in practice. In the exact-parameterized setting, where both the ground truth GMM and the learning model have the same number of components $m$, a vast line of work has aimed to establish rigorous recovery guarantees for EM. However, global convergence has only been proven for the case of $m=2$, and EM is known to fail to recover the ground truth when $m\geq 3$. In this paper, we consider the $\textit{over-parameterized}$ setting, where the learning model uses $n>m$ components to fit an $m$-component ground truth GMM. In contrast to the exact-parameterized case, we provide a rigorous global convergence guarantee for gradient EM. Specifically, for any well separated GMMs in general position, we prove that with only mild over-parameterization $n = \Omega(m\log m)$, randomly initialized gradient EM converges globally to the ground truth at a polynomial rate with polynomial samples. Our analysis proceeds in two stages and introduces a suite of novel tools for Gaussian Mixture analysis. We use Hermite polynomials to study the dynamics of gradient EM and employ tensor decomposition to characterize the geometric landscape of the likelihood loss. This is the first global convergence and recovery result for EM or Gradient EM beyond the special case of $m=2$.

Sharp Gap-Dependent Variance-Aware Regret Bounds for Tabular MDPs

We consider the gap-dependent regret bounds for episodic MDPs. We show that the Monotonic Value Propagation (MVP) algorithm achieves a variance-aware gap-dependent regret bound of $$\tilde{O}\left(\left(\sum_{\Delta_h(s,a)>0} \frac{H^2 \log K \land \mathtt{Var}_{\max}^{\text{c}}}{\Delta_h(s,a)} +\sum_{\Delta_h(s,a)=0}\frac{ H^2 \land \mathtt{Var}_{\max}^{\text{c}}}{\Delta_{\mathrm{min}}} + SAH^4 (S \lor H) \right) \log K\right),$$ where $H$ is the planning horizon, $S$ is the number of states, $A$ is the number of actions, and $K$ is the number of episodes. Here, $\Delta_h(s,a) =V_h^* (a) - Q_h^* (s, a)$ represents the suboptimality gap and $\Delta_{\mathrm{min}} := \min_{\Delta_h (s,a) > 0} \Delta_h(s,a)$. The term $\mathtt{Var}_{\max}^{\text{c}}$ denotes the maximum conditional total variance, calculated as the maximum over all $(\pi, h, s)$ tuples of the expected total variance under policy $\pi$ conditioned on trajectories visiting state $s$ at step $h$. $\mathtt{Var}_{\max}^{\text{c}}$ characterizes the maximum randomness encountered when learning any $(h, s)$ pair. Our result stems from a novel analysis of the weighted sum of the suboptimality gap and can be potentially adapted for other algorithms. To complement the study, we establish a lower bound of $$\Omega \left( \sum_{\Delta_h(s,a)>0} \frac{H^2 \land \mathtt{Var}_{\max}^{\text{c}}}{\Delta_h(s,a)}\cdot \log K\right),$$ demonstrating the necessity of dependence on $\mathtt{Var}_{\max}^{\text{c}}$ even when the maximum unconditional total variance (without conditioning on $(h, s)$) approaches zero.

Understanding the Performance Gap in Preference Learning: A Dichotomy of RLHF and DPO

We present a fine-grained theoretical analysis of the performance gap between reinforcement learning from human feedback (RLHF) and direct preference optimization (DPO) under a representation gap. Our study decomposes this gap into two sources: an explicit representation gap under exact optimization and an implicit representation gap under finite samples. In the exact optimization setting, we characterize how the relative capacities of the reward and policy model classes influence the final policy qualities. We show that RLHF, DPO, or online DPO can outperform one another depending on the type of model mis-specifications. Notably, online DPO can outperform both RLHF and standard DPO when the reward and policy model classes are isomorphic and both mis-specified. In the approximate optimization setting, we provide a concrete construction where the ground-truth reward is implicitly sparse and show that RLHF requires significantly fewer samples than DPO to recover an effective reward model -- highlighting a statistical advantage of two-stage learning. Together, these results provide a comprehensive understanding of the performance gap between RLHF and DPO under various settings, and offer practical insights into when each method is preferred.

Iteratively reweighted kernel machines efficiently learn sparse functions

The impressive practical performance of neural networks is often attributed to their ability to learn low-dimensional data representations and hierarchical structure directly from data. In this work, we argue that these two phenomena are not unique to neural networks, and can be elicited from classical kernel methods. Namely, we show that the derivative of the kernel predictor can detect the influential coordinates with low sample complexity. Moreover, by iteratively using the derivatives to reweight the data and retrain kernel machines, one is able to efficiently learn hierarchical polynomials with finite leap complexity. Numerical experiments illustrate the developed theory.

LoRe: Personalizing LLMs via Low-Rank Reward Modeling

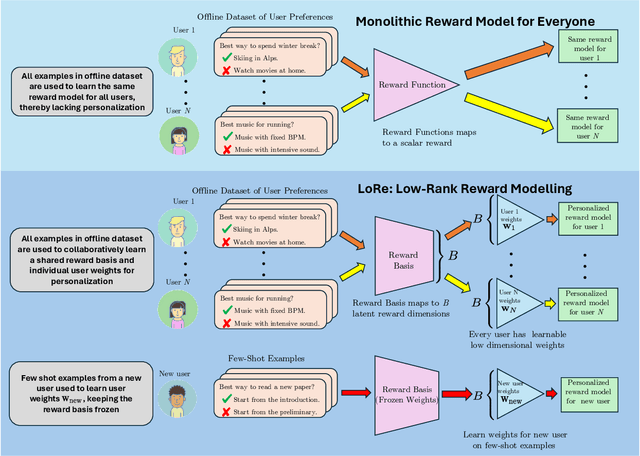
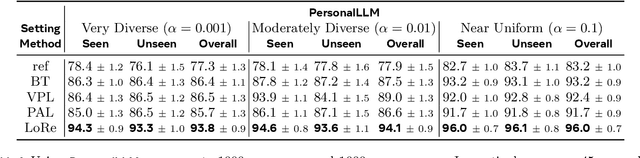
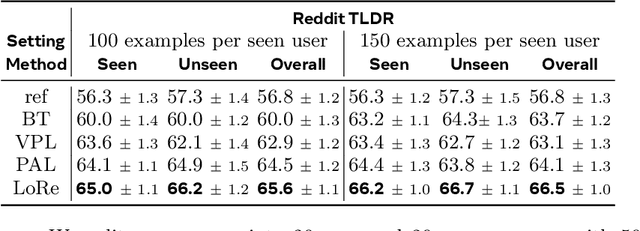
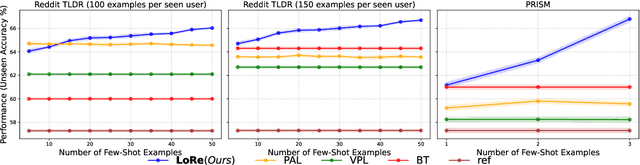
Personalizing large language models (LLMs) to accommodate diverse user preferences is essential for enhancing alignment and user satisfaction. Traditional reinforcement learning from human feedback (RLHF) approaches often rely on monolithic value representations, limiting their ability to adapt to individual preferences. We introduce a novel framework that leverages low-rank preference modeling to efficiently learn and generalize user-specific reward functions. By representing reward functions in a low-dimensional subspace and modeling individual preferences as weighted combinations of shared basis functions, our approach avoids rigid user categorization while enabling scalability and few-shot adaptation. We validate our method on multiple preference datasets, demonstrating superior generalization to unseen users and improved accuracy in preference prediction tasks.

Sub-optimality of the Separation Principle for Quadratic Control from Bilinear Observations

We consider the problem of controlling a linear dynamical system from bilinear observations with minimal quadratic cost. Despite the similarity of this problem to standard linear quadratic Gaussian (LQG) control, we show that when the observation model is bilinear, neither does the Separation Principle hold, nor is the optimal controller affine in the estimated state. Moreover, the cost-to-go is non-convex in the control input. Hence, finding an analytical expression for the optimal feedback controller is difficult in general. Under certain settings, we show that the standard LQG controller locally maximizes the cost instead of minimizing it. Furthermore, the optimal controllers (derived analytically) are not unique and are nonlinear in the estimated state. We also introduce a notion of input-dependent observability and derive conditions under which the Kalman filter covariance remains bounded. We illustrate our theoretical results through numerical experiments in multiple synthetic settings.

Gating is Weighting: Understanding Gated Linear Attention through In-context Learning

Linear attention methods offer a compelling alternative to softmax attention due to their efficiency in recurrent decoding. Recent research has focused on enhancing standard linear attention by incorporating gating while retaining its computational benefits. Such Gated Linear Attention (GLA) architectures include competitive models such as Mamba and RWKV. In this work, we investigate the in-context learning capabilities of the GLA model and make the following contributions. We show that a multilayer GLA can implement a general class of Weighted Preconditioned Gradient Descent (WPGD) algorithms with data-dependent weights. These weights are induced by the gating mechanism and the input, enabling the model to control the contribution of individual tokens to prediction. To further understand the mechanics of this weighting, we introduce a novel data model with multitask prompts and characterize the optimization landscape of learning a WPGD algorithm. Under mild conditions, we establish the existence and uniqueness (up to scaling) of a global minimum, corresponding to a unique WPGD solution. Finally, we translate these findings to explore the optimization landscape of GLA and shed light on how gating facilitates context-aware learning and when it is provably better than vanilla linear attention.

Extragradient Preference Optimization (EGPO): Beyond Last-Iterate Convergence for Nash Learning from Human Feedback

Reinforcement learning from human feedback (RLHF) has become essential for improving language model capabilities, but traditional approaches rely on the assumption that human preferences follow a transitive Bradley-Terry model. This assumption fails to capture the non-transitive nature of populational human preferences. Nash learning from human feedback (NLHF), targeting non-transitive preferences, is a problem of computing the Nash equilibrium (NE) of the two-player constant-sum game defined by the human preference. We introduce Extragradient preference optimization (EGPO), a novel algorithm for NLHF achieving last-iterate linear convergence to the NE of KL-regularized games and polynomial convergence to the NE of original games, while being robust to noise. Unlike previous approaches that rely on nested optimization, we derive an equivalent implementation using gradients of an online variant of the identity preference optimization (IPO) loss, enabling more faithful implementation for neural networks. Our empirical evaluations demonstrate EGPO's superior performance over baseline methods when training for the same number of epochs, as measured by pairwise win-rates using the ground truth preference. These results validate both the theoretical strengths and practical advantages of EGPO for language model alignment with non-transitive human preferences.

Keeping up with dynamic attackers: Certifying robustness to adaptive online data poisoning

The rise of foundation models fine-tuned on human feedback from potentially untrusted users has increased the risk of adversarial data poisoning, necessitating the study of robustness of learning algorithms against such attacks. Existing research on provable certified robustness against data poisoning attacks primarily focuses on certifying robustness for static adversaries who modify a fraction of the dataset used to train the model before the training algorithm is applied. In practice, particularly when learning from human feedback in an online sense, adversaries can observe and react to the learning process and inject poisoned samples that optimize adversarial objectives better than when they are restricted to poisoning a static dataset once, before the learning algorithm is applied. Indeed, it has been shown in prior work that online dynamic adversaries can be significantly more powerful than static ones. We present a novel framework for computing certified bounds on the impact of dynamic poisoning, and use these certificates to design robust learning algorithms. We give an illustration of the framework for the mean estimation and binary classification problems and outline directions for extending this in further work. The code to implement our certificates and replicate our results is available at https://github.com/Avinandan22/Certified-Robustness.