Sub-optimality of the Separation Principle for Quadratic Control from Bilinear Observations

We consider the problem of controlling a linear dynamical system from bilinear observations with minimal quadratic cost. Despite the similarity of this problem to standard linear quadratic Gaussian (LQG) control, we show that when the observation model is bilinear, neither does the Separation Principle hold, nor is the optimal controller affine in the estimated state. Moreover, the cost-to-go is non-convex in the control input. Hence, finding an analytical expression for the optimal feedback controller is difficult in general. Under certain settings, we show that the standard LQG controller locally maximizes the cost instead of minimizing it. Furthermore, the optimal controllers (derived analytically) are not unique and are nonlinear in the estimated state. We also introduce a notion of input-dependent observability and derive conditions under which the Kalman filter covariance remains bounded. We illustrate our theoretical results through numerical experiments in multiple synthetic settings.

Finite Sample Identification of Partially Observed Bilinear Dynamical Systems

We consider the problem of learning a realization of a partially observed bilinear dynamical system (BLDS) from noisy input-output data. Given a single trajectory of input-output samples, we provide a finite time analysis for learning the system's Markov-like parameters, from which a balanced realization of the bilinear system can be obtained. Our bilinear system identification algorithm learns the system's Markov-like parameters by regressing the outputs to highly correlated, nonlinear, and heavy-tailed covariates. Moreover, the stability of BLDS depends on the sequence of inputs used to excite the system. These properties, unique to partially observed bilinear dynamical systems, pose significant challenges to the analysis of our algorithm for learning the unknown dynamics. We address these challenges and provide high probability error bounds on our identification algorithm under a uniform stability assumption. Our analysis provides insights into system theoretic quantities that affect learning accuracy and sample complexity. Lastly, we perform numerical experiments with synthetic data to reinforce these insights.

Model-free Low-Rank Reinforcement Learning via Leveraged Entry-wise Matrix Estimation

We consider the problem of learning an $\varepsilon$-optimal policy in controlled dynamical systems with low-rank latent structure. For this problem, we present LoRa-PI (Low-Rank Policy Iteration), a model-free learning algorithm alternating between policy improvement and policy evaluation steps. In the latter, the algorithm estimates the low-rank matrix corresponding to the (state, action) value function of the current policy using the following two-phase procedure. The entries of the matrix are first sampled uniformly at random to estimate, via a spectral method, the leverage scores of its rows and columns. These scores are then used to extract a few important rows and columns whose entries are further sampled. The algorithm exploits these new samples to complete the matrix estimation using a CUR-like method. For this leveraged matrix estimation procedure, we establish entry-wise guarantees that remarkably, do not depend on the coherence of the matrix but only on its spikiness. These guarantees imply that LoRa-PI learns an $\varepsilon$-optimal policy using $\widetilde{O}({S+A\over \mathrm{poly}(1-\gamma)\varepsilon^2})$ samples where $S$ (resp. $A$) denotes the number of states (resp. actions) and $\gamma$ the discount factor. Our algorithm achieves this order-optimal (in $S$, $A$ and $\varepsilon$) sample complexity under milder conditions than those assumed in previously proposed approaches.

Learning Linear Dynamics from Bilinear Observations

We consider the problem of learning a realization of a partially observed dynamical system with linear state transitions and bilinear observations. Under very mild assumptions on the process and measurement noises, we provide a finite time analysis for learning the unknown dynamics matrices (up to a similarity transform). Our analysis involves a regression problem with heavy-tailed and dependent data. Moreover, each row of our design matrix contains a Kronecker product of current input with a history of inputs, making it difficult to guarantee persistence of excitation. We overcome these challenges, first providing a data-dependent high probability error bound for arbitrary but fixed inputs. Then, we derive a data-independent error bound for inputs chosen according to a simple random design. Our main results provide an upper bound on the statistical error rates and sample complexity of learning the unknown dynamics matrices from a single finite trajectory of bilinear observations.

Low-Rank Bandits via Tight Two-to-Infinity Singular Subspace Recovery

We study contextual bandits with low-rank structure where, in each round, if the (context, arm) pair $(i,j)\in [m]\times [n]$ is selected, the learner observes a noisy sample of the $(i,j)$-th entry of an unknown low-rank reward matrix. Successive contexts are generated randomly in an i.i.d. manner and are revealed to the learner. For such bandits, we present efficient algorithms for policy evaluation, best policy identification and regret minimization. For policy evaluation and best policy identification, we show that our algorithms are nearly minimax optimal. For instance, the number of samples required to return an $\varepsilon$-optimal policy with probability at least $1-\delta$ typically scales as ${m+n\over \varepsilon^2}\log(1/\delta)$. Our regret minimization algorithm enjoys minimax guarantees scaling as $r^{7/4}(m+n)^{3/4}\sqrt{T}$, which improves over existing algorithms. All the proposed algorithms consist of two phases: they first leverage spectral methods to estimate the left and right singular subspaces of the low-rank reward matrix. We show that these estimates enjoy tight error guarantees in the two-to-infinity norm. This in turn allows us to reformulate our problems as a misspecified linear bandit problem with dimension roughly $r(m+n)$ and misspecification controlled by the subspace recovery error, as well as to design the second phase of our algorithms efficiently.

Spectral Entry-wise Matrix Estimation for Low-Rank Reinforcement Learning

We study matrix estimation problems arising in reinforcement learning (RL) with low-rank structure. In low-rank bandits, the matrix to be recovered specifies the expected arm rewards, and for low-rank Markov Decision Processes (MDPs), it may for example characterize the transition kernel of the MDP. In both cases, each entry of the matrix carries important information, and we seek estimation methods with low entry-wise error. Importantly, these methods further need to accommodate for inherent correlations in the available data (e.g. for MDPs, the data consists of system trajectories). We investigate the performance of simple spectral-based matrix estimation approaches: we show that they efficiently recover the singular subspaces of the matrix and exhibit nearly-minimal entry-wise error. These new results on low-rank matrix estimation make it possible to devise reinforcement learning algorithms that fully exploit the underlying low-rank structure. We provide two examples of such algorithms: a regret minimization algorithm for low-rank bandit problems, and a best policy identification algorithm for reward-free RL in low-rank MDPs. Both algorithms yield state-of-the-art performance guarantees.

A Tutorial on the Non-Asymptotic Theory of System Identification

This tutorial serves as an introduction to recently developed non-asymptotic methods in the theory of -- mainly linear -- system identification. We emphasize tools we deem particularly useful for a range of problems in this domain, such as the covering technique, the Hanson-Wright Inequality and the method of self-normalized martingales. We then employ these tools to give streamlined proofs of the performance of various least-squares based estimators for identifying the parameters in autoregressive models. We conclude by sketching out how the ideas presented herein can be extended to certain nonlinear identification problems.

Nearly Optimal Latent State Decoding in Block MDPs

We investigate the problems of model estimation and reward-free learning in episodic Block MDPs. In these MDPs, the decision maker has access to rich observations or contexts generated from a small number of latent states. We are first interested in estimating the latent state decoding function (the mapping from the observations to latent states) based on data generated under a fixed behavior policy. We derive an information-theoretical lower bound on the error rate for estimating this function and present an algorithm approaching this fundamental limit. In turn, our algorithm also provides estimates of all the components of the MDP. We then study the problem of learning near-optimal policies in the reward-free framework. Based on our efficient model estimation algorithm, we show that we can infer a policy converging (as the number of collected samples grows large) to the optimal policy at the best possible rate. Interestingly, our analysis provides necessary and sufficient conditions under which exploiting the block structure yields improvements in the sample complexity for identifying near-optimal policies. When these conditions are met, the sample complexity in the minimax reward-free setting is improved by a multiplicative factor $n$, where $n$ is the number of possible contexts.

Best Policy Identification in Linear MDPs

We investigate the problem of best policy identification in discounted linear Markov Decision Processes in the fixed confidence setting under a generative model. We first derive an instance-specific lower bound on the expected number of samples required to identify an $\varepsilon$-optimal policy with probability $1-\delta$. The lower bound characterizes the optimal sampling rule as the solution of an intricate non-convex optimization program, but can be used as the starting point to devise simple and near-optimal sampling rules and algorithms. We devise such algorithms. One of these exhibits a sample complexity upper bounded by ${\cal O}({\frac{d}{(\varepsilon+\Delta)^2}} (\log(\frac{1}{\delta})+d))$ where $\Delta$ denotes the minimum reward gap of sub-optimal actions and $d$ is the dimension of the feature space. This upper bound holds in the moderate-confidence regime (i.e., for all $\delta$), and matches existing minimax and gap-dependent lower bounds. We extend our algorithm to episodic linear MDPs.

Learning Optimal Antenna Tilt Control Policies: A Contextual Linear Bandit Approach

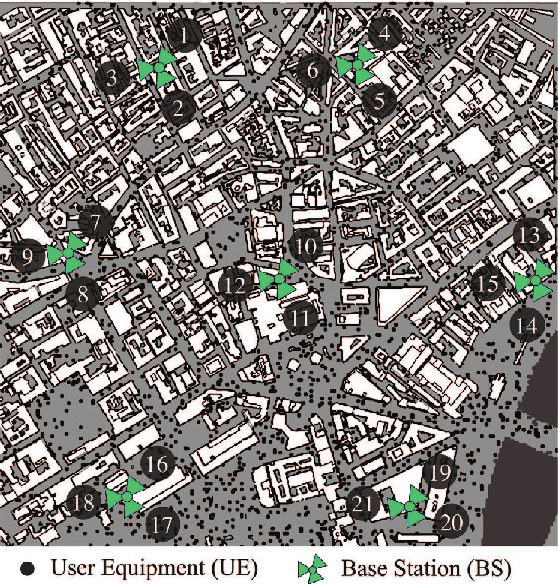
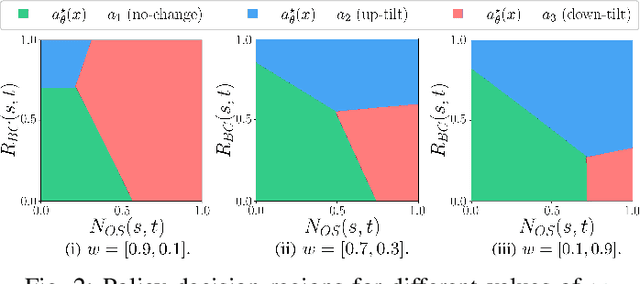
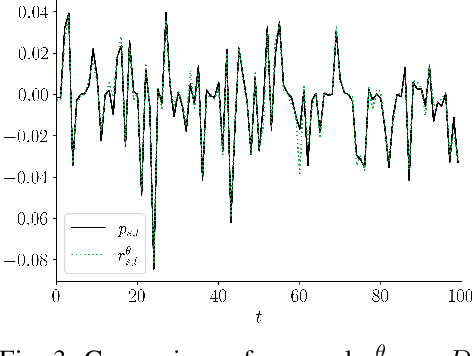
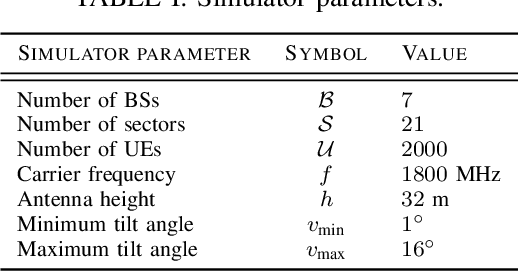
Controlling antenna tilts in cellular networks is imperative to reach an efficient trade-off between network coverage and capacity. In this paper, we devise algorithms learning optimal tilt control policies from existing data (in the so-called passive learning setting) or from data actively generated by the algorithms (the active learning setting). We formalize the design of such algorithms as a Best Policy Identification (BPI) problem in Contextual Linear Multi-Arm Bandits (CL-MAB). An arm represents an antenna tilt update; the context captures current network conditions; the reward corresponds to an improvement of performance, mixing coverage and capacity; and the objective is to identify, with a given level of confidence, an approximately optimal policy (a function mapping the context to an arm with maximal reward). For CL-MAB in both active and passive learning settings, we derive information-theoretical lower bounds on the number of samples required by any algorithm returning an approximately optimal policy with a given level of certainty, and devise algorithms achieving these fundamental limits. We apply our algorithms to the Remote Electrical Tilt (RET) optimization problem in cellular networks, and show that they can produce optimal tilt update policy using much fewer data samples than naive or existing rule-based learning algorithms.