Nikolai Matni
Occupancy-aware Trajectory Planning for Autonomous Valet Parking in Uncertain Dynamic Environments
Sep 11, 2025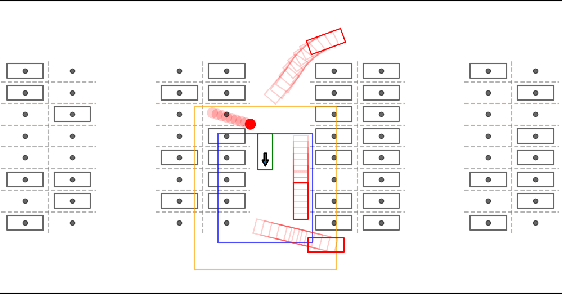
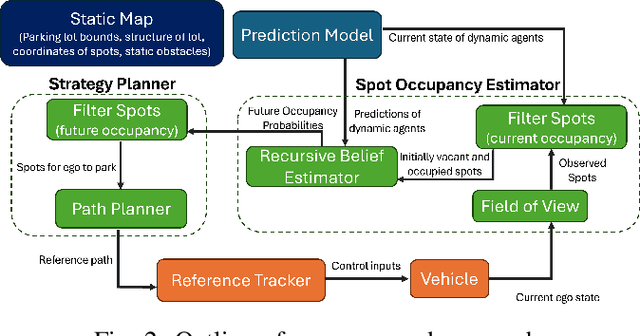
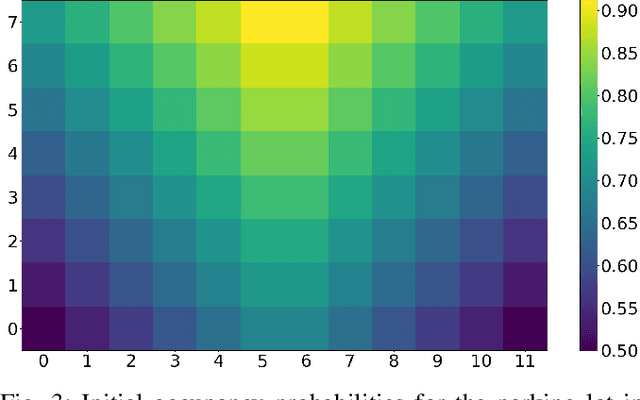
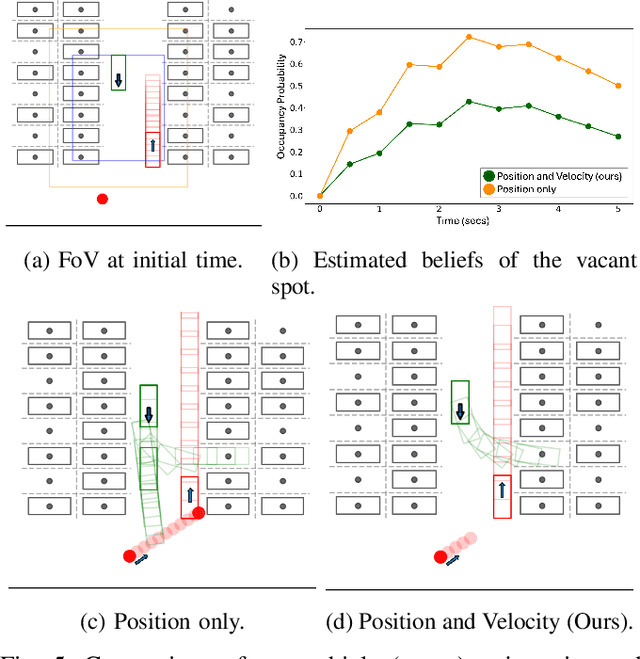
Abstract:Accurately reasoning about future parking spot availability and integrated planning is critical for enabling safe and efficient autonomous valet parking in dynamic, uncertain environments. Unlike existing methods that rely solely on instantaneous observations or static assumptions, we present an approach that predicts future parking spot occupancy by explicitly distinguishing between initially vacant and occupied spots, and by leveraging the predicted motion of dynamic agents. We introduce a probabilistic spot occupancy estimator that incorporates partial and noisy observations within a limited Field-of-View (FoV) model and accounts for the evolving uncertainty of unobserved regions. Coupled with this, we design a strategy planner that adaptively balances goal-directed parking maneuvers with exploratory navigation based on information gain, and intelligently incorporates wait-and-go behaviors at promising spots. Through randomized simulations emulating large parking lots, we demonstrate that our framework significantly improves parking efficiency, safety margins, and trajectory smoothness compared to existing approaches.
Quad-LCD: Layered Control Decomposition Enables Actuator-Feasible Quadrotor Trajectory Planning
May 15, 2025Abstract:In this work, we specialize contributions from prior work on data-driven trajectory generation for a quadrotor system with motor saturation constraints. When motors saturate in quadrotor systems, there is an ``uncontrolled drift" of the vehicle that results in a crash. To tackle saturation, we apply a control decomposition and learn a tracking penalty from simulation data consisting of low, medium and high-cost reference trajectories. Our approach reduces crash rates by around $49\%$ compared to baselines on aggressive maneuvers in simulation. On the Crazyflie hardware platform, we demonstrate feasibility through experiments that lead to successful flights. Motivated by the growing interest in data-driven methods to quadrotor planning, we provide open-source lightweight code with an easy-to-use abstraction of hardware platforms.
* 4 pages, 4 figures
Graph-based Path Planning with Dynamic Obstacle Avoidance for Autonomous Parking
Apr 17, 2025Abstract:Safe and efficient path planning in parking scenarios presents a significant challenge due to the presence of cluttered environments filled with static and dynamic obstacles. To address this, we propose a novel and computationally efficient planning strategy that seamlessly integrates the predictions of dynamic obstacles into the planning process, ensuring the generation of collision-free paths. Our approach builds upon the conventional Hybrid A star algorithm by introducing a time-indexed variant that explicitly accounts for the predictions of dynamic obstacles during node exploration in the graph, thus enabling dynamic obstacle avoidance. We integrate the time-indexed Hybrid A star algorithm within an online planning framework to compute local paths at each planning step, guided by an adaptively chosen intermediate goal. The proposed method is validated in diverse parking scenarios, including perpendicular, angled, and parallel parking. Through simulations, we showcase our approach's potential in greatly improving the efficiency and safety when compared to the state of the art spline-based planning method for parking situations.
Learning with Imperfect Models: When Multi-step Prediction Mitigates Compounding Error
Apr 02, 2025Abstract:Compounding error, where small prediction mistakes accumulate over time, presents a major challenge in learning-based control. For example, this issue often limits the performance of model-based reinforcement learning and imitation learning. One common approach to mitigate compounding error is to train multi-step predictors directly, rather than relying on autoregressive rollout of a single-step model. However, it is not well understood when the benefits of multi-step prediction outweigh the added complexity of learning a more complicated model. In this work, we provide a rigorous analysis of this trade-off in the context of linear dynamical systems. We show that when the model class is well-specified and accurately captures the system dynamics, single-step models achieve lower asymptotic prediction error. On the other hand, when the model class is misspecified due to partial observability, direct multi-step predictors can significantly reduce bias and thus outperform single-step approaches. These theoretical results are supported by numerical experiments, wherein we also (a) empirically evaluate an intermediate strategy which trains a single-step model using a multi-step loss and (b) evaluate performance of single step and multi-step predictors in a closed loop control setting.
Policy Gradient for LQR with Domain Randomization
Mar 31, 2025Abstract:Domain randomization (DR) enables sim-to-real transfer by training controllers on a distribution of simulated environments, with the goal of achieving robust performance in the real world. Although DR is widely used in practice and is often solved using simple policy gradient (PG) methods, understanding of its theoretical guarantees remains limited. Toward addressing this gap, we provide the first convergence analysis of PG methods for domain-randomized linear quadratic regulation (LQR). We show that PG converges globally to the minimizer of a finite-sample approximation of the DR objective under suitable bounds on the heterogeneity of the sampled systems. We also quantify the sample-complexity associated with achieving a small performance gap between the sample-average and population-level objectives. Additionally, we propose and analyze a discount-factor annealing algorithm that obviates the need for an initial jointly stabilizing controller, which may be challenging to find. Empirical results support our theoretical findings and highlight promising directions for future work, including risk-sensitive DR formulations and stochastic PG algorithms.
ADMM-MCBF-LCA: A Layered Control Architecture for Safe Real-Time Navigation
Mar 04, 2025Abstract:We consider the problem of safe real-time navigation of a robot in a dynamic environment with moving obstacles of arbitrary smooth geometries and input saturation constraints. We assume that the robot detects and models nearby obstacle boundaries with a short-range sensor and that this detection is error-free. This problem presents three main challenges: i) input constraints, ii) safety, and iii) real-time computation. To tackle all three challenges, we present a layered control architecture (LCA) consisting of an offline path library generation layer, and an online path selection and safety layer. To overcome the limitations of reactive methods, our offline path library consists of feasible controllers, feedback gains, and reference trajectories. To handle computational burden and safety, we solve online path selection and generate safe inputs that run at 100 Hz. Through simulations on Gazebo and Fetch hardware in an indoor environment, we evaluate our approach against baselines that are layered, end-to-end, or reactive. Our experiments demonstrate that among all algorithms, only our proposed LCA is able to complete tasks such as reaching a goal, safely. When comparing metrics such as safety, input error, and success rate, we show that our approach generates safe and feasible inputs throughout the robot execution.
On The Concurrence of Layer-wise Preconditioning Methods and Provable Feature Learning
Feb 03, 2025
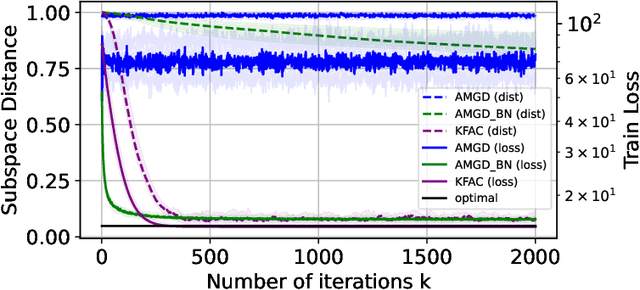
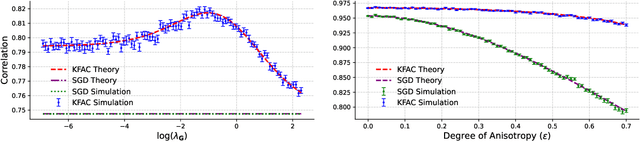

Abstract:Layer-wise preconditioning methods are a family of memory-efficient optimization algorithms that introduce preconditioners per axis of each layer's weight tensors. These methods have seen a recent resurgence, demonstrating impressive performance relative to entry-wise ("diagonal") preconditioning methods such as Adam(W) on a wide range of neural network optimization tasks. Complementary to their practical performance, we demonstrate that layer-wise preconditioning methods are provably necessary from a statistical perspective. To showcase this, we consider two prototypical models, linear representation learning and single-index learning, which are widely used to study how typical algorithms efficiently learn useful features to enable generalization. In these problems, we show SGD is a suboptimal feature learner when extending beyond ideal isotropic inputs $\mathbf{x} \sim \mathsf{N}(\mathbf{0}, \mathbf{I})$ and well-conditioned settings typically assumed in prior work. We demonstrate theoretically and numerically that this suboptimality is fundamental, and that layer-wise preconditioning emerges naturally as the solution. We further show that standard tools like Adam preconditioning and batch-norm only mildly mitigate these issues, supporting the unique benefits of layer-wise preconditioning.
Logarithmic Regret for Nonlinear Control
Jan 17, 2025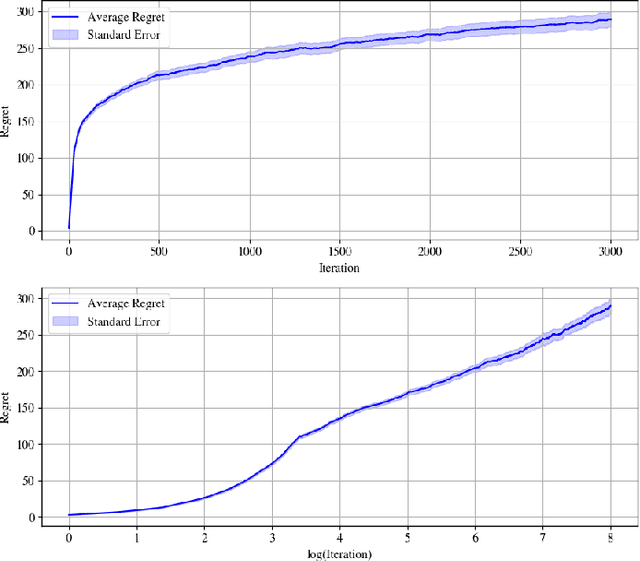
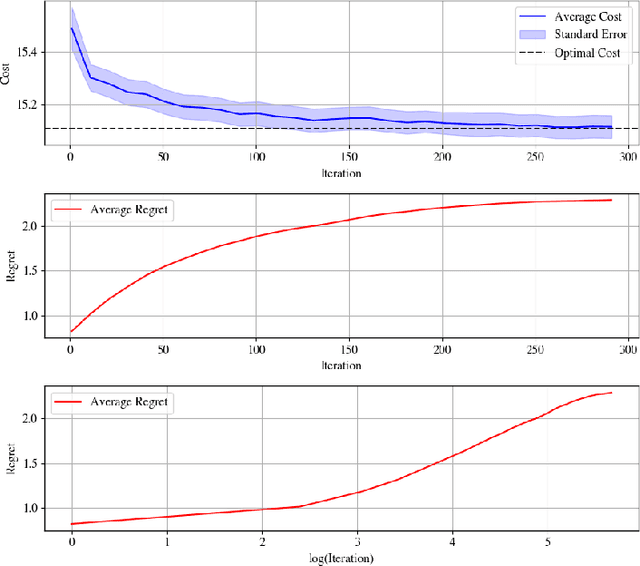
Abstract:We address the problem of learning to control an unknown nonlinear dynamical system through sequential interactions. Motivated by high-stakes applications in which mistakes can be catastrophic, such as robotics and healthcare, we study situations where it is possible for fast sequential learning to occur. Fast sequential learning is characterized by the ability of the learning agent to incur logarithmic regret relative to a fully-informed baseline. We demonstrate that fast sequential learning is achievable in a diverse class of continuous control problems where the system dynamics depend smoothly on unknown parameters, provided the optimal control policy is persistently exciting. Additionally, we derive a regret bound which grows with the square root of the number of interactions for cases where the optimal policy is not persistently exciting. Our results provide the first regret bounds for controlling nonlinear dynamical systems depending nonlinearly on unknown parameters. We validate the trends our theory predicts in simulation on a simple dynamical system.
Monocular Event-Based Vision for Obstacle Avoidance with a Quadrotor
Nov 05, 2024

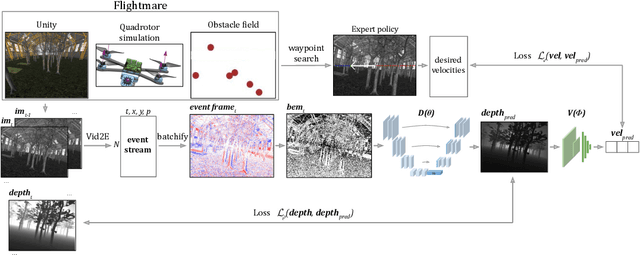
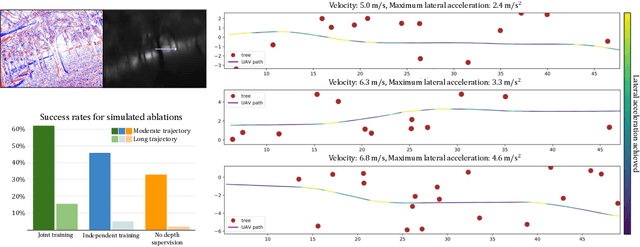
Abstract:We present the first static-obstacle avoidance method for quadrotors using just an onboard, monocular event camera. Quadrotors are capable of fast and agile flight in cluttered environments when piloted manually, but vision-based autonomous flight in unknown environments is difficult in part due to the sensor limitations of traditional onboard cameras. Event cameras, however, promise nearly zero motion blur and high dynamic range, but produce a very large volume of events under significant ego-motion and further lack a continuous-time sensor model in simulation, making direct sim-to-real transfer not possible. By leveraging depth prediction as a pretext task in our learning framework, we can pre-train a reactive obstacle avoidance events-to-control policy with approximated, simulated events and then fine-tune the perception component with limited events-and-depth real-world data to achieve obstacle avoidance in indoor and outdoor settings. We demonstrate this across two quadrotor-event camera platforms in multiple settings and find, contrary to traditional vision-based works, that low speeds (1m/s) make the task harder and more prone to collisions, while high speeds (5m/s) result in better event-based depth estimation and avoidance. We also find that success rates in outdoor scenes can be significantly higher than in certain indoor scenes.
* 18 pages with supplementary
Guarantees for Nonlinear Representation Learning: Non-identical Covariates, Dependent Data, Fewer Samples
Oct 15, 2024


Abstract:A driving force behind the diverse applicability of modern machine learning is the ability to extract meaningful features across many sources. However, many practical domains involve data that are non-identically distributed across sources, and statistically dependent within its source, violating vital assumptions in existing theoretical studies. Toward addressing these issues, we establish statistical guarantees for learning general $\textit{nonlinear}$ representations from multiple data sources that admit different input distributions and possibly dependent data. Specifically, we study the sample-complexity of learning $T+1$ functions $f_\star^{(t)} \circ g_\star$ from a function class $\mathcal F \times \mathcal G$, where $f_\star^{(t)}$ are task specific linear functions and $g_\star$ is a shared nonlinear representation. A representation $\hat g$ is estimated using $N$ samples from each of $T$ source tasks, and a fine-tuning function $\hat f^{(0)}$ is fit using $N'$ samples from a target task passed through $\hat g$. We show that when $N \gtrsim C_{\mathrm{dep}} (\mathrm{dim}(\mathcal F) + \mathrm{C}(\mathcal G)/T)$, the excess risk of $\hat f^{(0)} \circ \hat g$ on the target task decays as $\nu_{\mathrm{div}} \big(\frac{\mathrm{dim}(\mathcal F)}{N'} + \frac{\mathrm{C}(\mathcal G)}{N T} \big)$, where $C_{\mathrm{dep}}$ denotes the effect of data dependency, $\nu_{\mathrm{div}}$ denotes an (estimatable) measure of $\textit{task-diversity}$ between the source and target tasks, and $\mathrm C(\mathcal G)$ denotes the complexity of the representation class $\mathcal G$. In particular, our analysis reveals: as the number of tasks $T$ increases, both the sample requirement and risk bound converge to that of $r$-dimensional regression as if $g_\star$ had been given, and the effect of dependency only enters the sample requirement, leaving the risk bound matching the iid setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge