Logarithmic Regret for Nonlinear Control
Paper and Code
Jan 17, 2025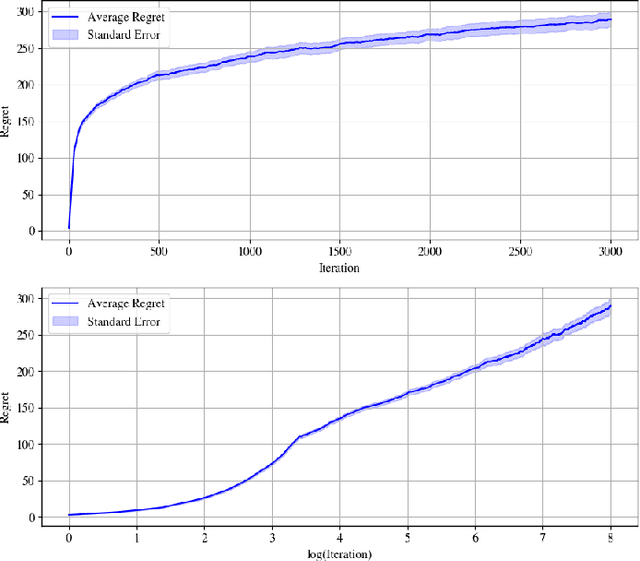
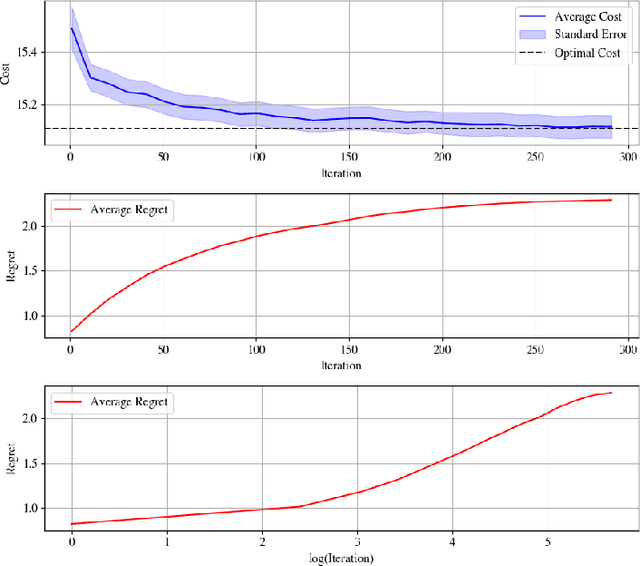
We address the problem of learning to control an unknown nonlinear dynamical system through sequential interactions. Motivated by high-stakes applications in which mistakes can be catastrophic, such as robotics and healthcare, we study situations where it is possible for fast sequential learning to occur. Fast sequential learning is characterized by the ability of the learning agent to incur logarithmic regret relative to a fully-informed baseline. We demonstrate that fast sequential learning is achievable in a diverse class of continuous control problems where the system dynamics depend smoothly on unknown parameters, provided the optimal control policy is persistently exciting. Additionally, we derive a regret bound which grows with the square root of the number of interactions for cases where the optimal policy is not persistently exciting. Our results provide the first regret bounds for controlling nonlinear dynamical systems depending nonlinearly on unknown parameters. We validate the trends our theory predicts in simulation on a simple dynamical system.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge