On The Concurrence of Layer-wise Preconditioning Methods and Provable Feature Learning

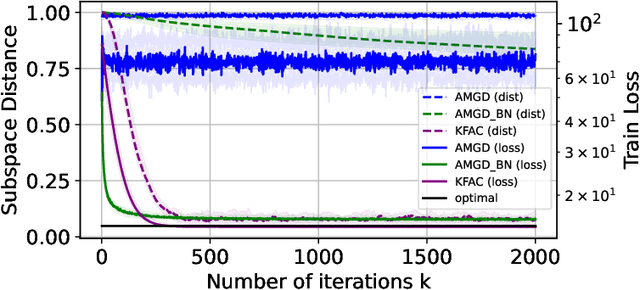
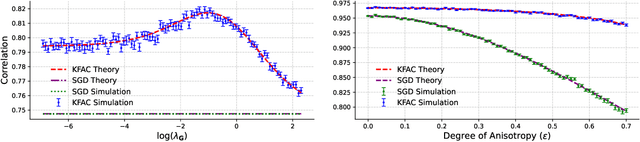
Layer-wise preconditioning methods are a family of memory-efficient optimization algorithms that introduce preconditioners per axis of each layer's weight tensors. These methods have seen a recent resurgence, demonstrating impressive performance relative to entry-wise ("diagonal") preconditioning methods such as Adam(W) on a wide range of neural network optimization tasks. Complementary to their practical performance, we demonstrate that layer-wise preconditioning methods are provably necessary from a statistical perspective. To showcase this, we consider two prototypical models, linear representation learning and single-index learning, which are widely used to study how typical algorithms efficiently learn useful features to enable generalization. In these problems, we show SGD is a suboptimal feature learner when extending beyond ideal isotropic inputs $\mathbf{x} \sim \mathsf{N}(\mathbf{0}, \mathbf{I})$ and well-conditioned settings typically assumed in prior work. We demonstrate theoretically and numerically that this suboptimality is fundamental, and that layer-wise preconditioning emerges naturally as the solution. We further show that standard tools like Adam preconditioning and batch-norm only mildly mitigate these issues, supporting the unique benefits of layer-wise preconditioning.

Guarantees for Nonlinear Representation Learning: Non-identical Covariates, Dependent Data, Fewer Samples

A driving force behind the diverse applicability of modern machine learning is the ability to extract meaningful features across many sources. However, many practical domains involve data that are non-identically distributed across sources, and statistically dependent within its source, violating vital assumptions in existing theoretical studies. Toward addressing these issues, we establish statistical guarantees for learning general $\textit{nonlinear}$ representations from multiple data sources that admit different input distributions and possibly dependent data. Specifically, we study the sample-complexity of learning $T+1$ functions $f_\star^{(t)} \circ g_\star$ from a function class $\mathcal F \times \mathcal G$, where $f_\star^{(t)}$ are task specific linear functions and $g_\star$ is a shared nonlinear representation. A representation $\hat g$ is estimated using $N$ samples from each of $T$ source tasks, and a fine-tuning function $\hat f^{(0)}$ is fit using $N'$ samples from a target task passed through $\hat g$. We show that when $N \gtrsim C_{\mathrm{dep}} (\mathrm{dim}(\mathcal F) + \mathrm{C}(\mathcal G)/T)$, the excess risk of $\hat f^{(0)} \circ \hat g$ on the target task decays as $\nu_{\mathrm{div}} \big(\frac{\mathrm{dim}(\mathcal F)}{N'} + \frac{\mathrm{C}(\mathcal G)}{N T} \big)$, where $C_{\mathrm{dep}}$ denotes the effect of data dependency, $\nu_{\mathrm{div}}$ denotes an (estimatable) measure of $\textit{task-diversity}$ between the source and target tasks, and $\mathrm C(\mathcal G)$ denotes the complexity of the representation class $\mathcal G$. In particular, our analysis reveals: as the number of tasks $T$ increases, both the sample requirement and risk bound converge to that of $r$-dimensional regression as if $g_\star$ had been given, and the effect of dependency only enters the sample requirement, leaving the risk bound matching the iid setting.

Regret Analysis of Multi-task Representation Learning for Linear-Quadratic Adaptive Control

Representation learning is a powerful tool that enables learning over large multitudes of agents or domains by enforcing that all agents operate on a shared set of learned features. However, many robotics or controls applications that would benefit from collaboration operate in settings with changing environments and goals, whereas most guarantees for representation learning are stated for static settings. Toward rigorously establishing the benefit of representation learning in dynamic settings, we analyze the regret of multi-task representation learning for linear-quadratic control. This setting introduces unique challenges. Firstly, we must account for and balance the $\textit{misspecification}$ introduced by an approximate representation. Secondly, we cannot rely on the parameter update schemes of single-task online LQR, for which least-squares often suffices, and must devise a novel scheme to ensure sufficient improvement. We demonstrate that for settings where exploration is "benign", the regret of any agent after $T$ timesteps scales as $\tilde O(\sqrt{T/H})$, where $H$ is the number of agents. In settings with "difficult" exploration, the regret scales as $\tilde{\mathcal O}(\sqrt{d_u d_\theta} \sqrt{T} + T^{3/4}/H^{1/5})$, where $d_x$ is the state-space dimension, $d_u$ is the input dimension, and $d_\theta$ is the task-specific parameter count. In both cases, by comparing to the minimax single-task regret $\tilde{\mathcal O}(\sqrt{d_x d_u^2}\sqrt{T})$, we see a benefit of a large number of agents. Notably, in the difficult exploration case, by sharing a representation across tasks, the effective task-specific parameter count can often be small $d_\theta < d_x d_u$. Lastly, we provide numerical validation of the trends we predict.

Multi-Task Imitation Learning for Linear Dynamical Systems

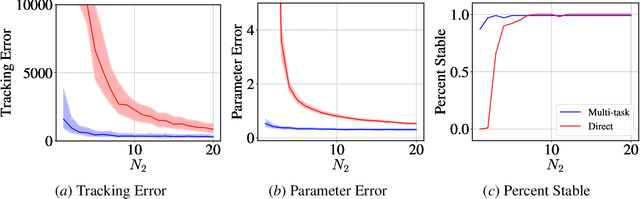
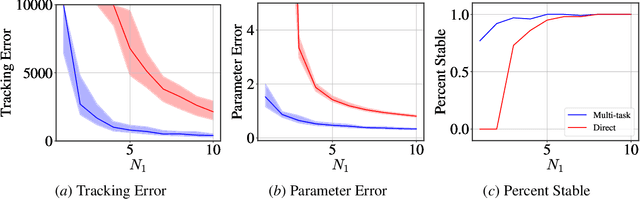
We study representation learning for efficient imitation learning over linear systems. In particular, we consider a setting where learning is split into two phases: (a) a pre-training step where a shared $k$-dimensional representation is learned from $H$ source policies, and (b) a target policy fine-tuning step where the learned representation is used to parameterize the policy class. We find that the imitation gap over trajectories generated by the learned target policy is bounded by $\tilde{O}\left( \frac{k n_x}{HN_{\mathrm{shared}}} + \frac{k n_u}{N_{\mathrm{target}}}\right)$, where $n_x > k$ is the state dimension, $n_u$ is the input dimension, $N_{\mathrm{shared}}$ denotes the total amount of data collected for each policy during representation learning, and $N_{\mathrm{target}}$ is the amount of target task data. This result formalizes the intuition that aggregating data across related tasks to learn a representation can significantly improve the sample efficiency of learning a target task. The trends suggested by this bound are corroborated in simulation.