T-FIX: Text-Based Explanations with Features Interpretable to eXperts

As LLMs are deployed in knowledge-intensive settings (e.g., surgery, astronomy, therapy), users expect not just answers, but also meaningful explanations for those answers. In these settings, users are often domain experts (e.g., doctors, astrophysicists, psychologists) who require explanations that reflect expert-level reasoning. However, current evaluation schemes primarily emphasize plausibility or internal faithfulness of the explanation, which fail to capture whether the content of the explanation truly aligns with expert intuition. We formalize expert alignment as a criterion for evaluating explanations with T-FIX, a benchmark spanning seven knowledge-intensive domains. In collaboration with domain experts, we develop novel metrics to measure the alignment of LLM explanations with expert judgment.

Probabilistic Stability Guarantees for Feature Attributions

Stability guarantees are an emerging tool for evaluating feature attributions, but existing certification methods rely on smoothed classifiers and often yield conservative guarantees. To address these limitations, we introduce soft stability and propose a simple, model-agnostic, and sample-efficient stability certification algorithm (SCA) that provides non-trivial and interpretable guarantees for any attribution. Moreover, we show that mild smoothing enables a graceful tradeoff between accuracy and stability, in contrast to prior certification methods that require a more aggressive compromise. Using Boolean function analysis, we give a novel characterization of stability under smoothing. We evaluate SCA on vision and language tasks, and demonstrate the effectiveness of soft stability in measuring the robustness of explanation methods.

On The Concurrence of Layer-wise Preconditioning Methods and Provable Feature Learning

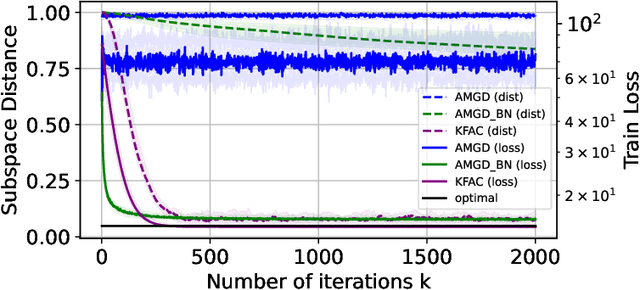
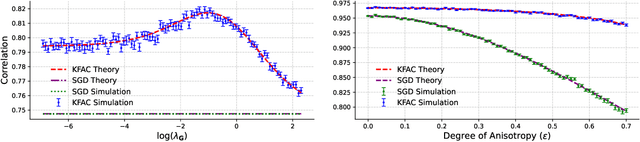
Layer-wise preconditioning methods are a family of memory-efficient optimization algorithms that introduce preconditioners per axis of each layer's weight tensors. These methods have seen a recent resurgence, demonstrating impressive performance relative to entry-wise ("diagonal") preconditioning methods such as Adam(W) on a wide range of neural network optimization tasks. Complementary to their practical performance, we demonstrate that layer-wise preconditioning methods are provably necessary from a statistical perspective. To showcase this, we consider two prototypical models, linear representation learning and single-index learning, which are widely used to study how typical algorithms efficiently learn useful features to enable generalization. In these problems, we show SGD is a suboptimal feature learner when extending beyond ideal isotropic inputs $\mathbf{x} \sim \mathsf{N}(\mathbf{0}, \mathbf{I})$ and well-conditioned settings typically assumed in prior work. We demonstrate theoretically and numerically that this suboptimality is fundamental, and that layer-wise preconditioning emerges naturally as the solution. We further show that standard tools like Adam preconditioning and batch-norm only mildly mitigate these issues, supporting the unique benefits of layer-wise preconditioning.

AR-Pro: Counterfactual Explanations for Anomaly Repair with Formal Properties

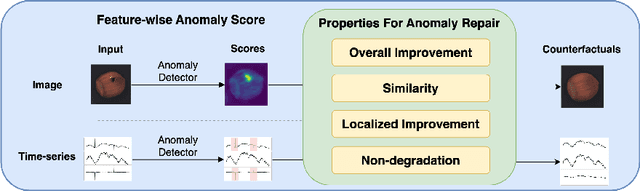
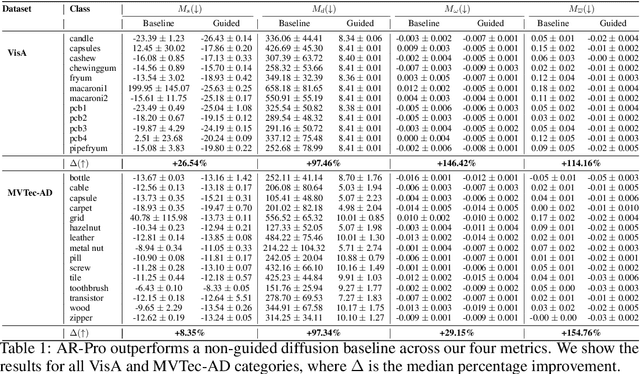
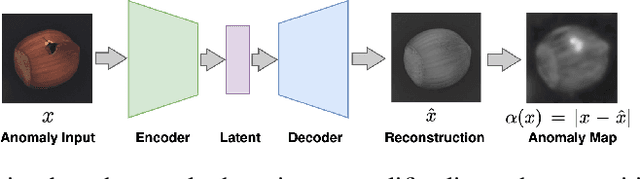
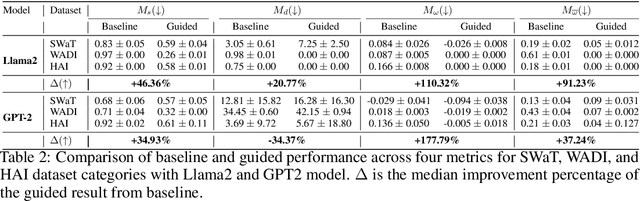
Anomaly detection is widely used for identifying critical errors and suspicious behaviors, but current methods lack interpretability. We leverage common properties of existing methods and recent advances in generative models to introduce counterfactual explanations for anomaly detection. Given an input, we generate its counterfactual as a diffusion-based repair that shows what a non-anomalous version should have looked like. A key advantage of this approach is that it enables a domain-independent formal specification of explainability desiderata, offering a unified framework for generating and evaluating explanations. We demonstrate the effectiveness of our anomaly explainability framework, AR-Pro, on vision (MVTec, VisA) and time-series (SWaT, WADI, HAI) anomaly datasets. The code used for the experiments is accessible at: https://github.com/xjiae/arpro.

The FIX Benchmark: Extracting Features Interpretable to eXperts

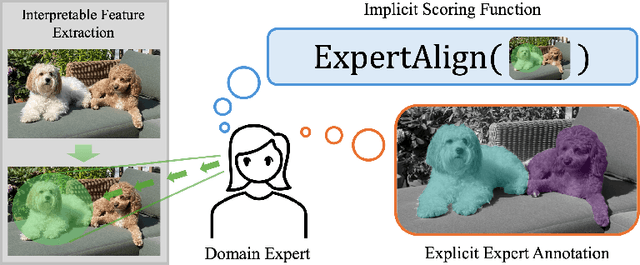
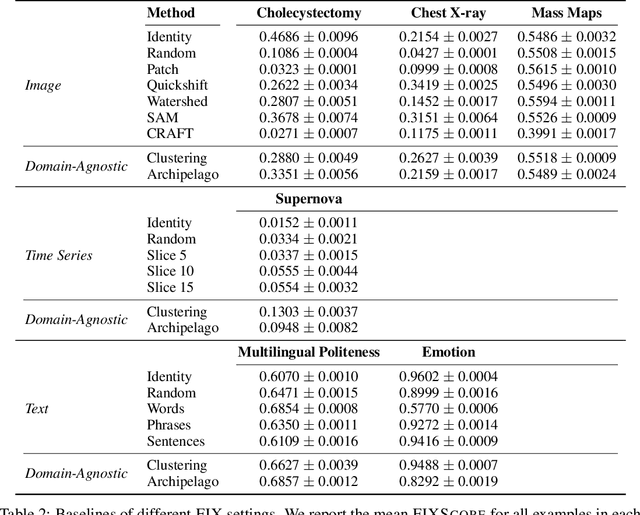
Feature-based methods are commonly used to explain model predictions, but these methods often implicitly assume that interpretable features are readily available. However, this is often not the case for high-dimensional data, and it can be hard even for domain experts to mathematically specify which features are important. Can we instead automatically extract collections or groups of features that are aligned with expert knowledge? To address this gap, we present FIX (Features Interpretable to eXperts), a benchmark for measuring how well a collection of features aligns with expert knowledge. In collaboration with domain experts, we have developed feature interpretability objectives across diverse real-world settings and unified them into a single framework that is the FIX benchmark. We find that popular feature-based explanation methods have poor alignment with expert-specified knowledge, highlighting the need for new methods that can better identify features interpretable to experts.

Logicbreaks: A Framework for Understanding Subversion of Rule-based Inference

We study how to subvert language models from following the rules. We model rule-following as inference in propositional Horn logic, a mathematical system in which rules have the form "if $P$ and $Q$, then $R$" for some propositions $P$, $Q$, and $R$. We prove that although transformers can faithfully abide by such rules, maliciously crafted prompts can nevertheless mislead even theoretically constructed models. Empirically, we find that attacks on our theoretical models mirror popular attacks on large language models. Our work suggests that studying smaller theoretical models can help understand the behavior of large language models in rule-based settings like logical reasoning and jailbreak attacks.

Stability Guarantees for Feature Attributions with Multiplicative Smoothing

Explanation methods for machine learning models tend to not provide any formal guarantees and may not reflect the underlying decision-making process. In this work, we analyze stability as a property for reliable feature attribution methods. We prove that relaxed variants of stability are guaranteed if the model is sufficiently Lipschitz with respect to the masking of features. To achieve such a model, we develop a smoothing method called Multiplicative Smoothing (MuS). We show that MuS overcomes theoretical limitations of standard smoothing techniques and can be integrated with any classifier and feature attribution method. We evaluate MuS on vision and language models with a variety of feature attribution methods, such as LIME and SHAP, and demonstrate that MuS endows feature attributions with non-trivial stability guarantees.

Parametric Chordal Sparsity for SDP-based Neural Network Verification

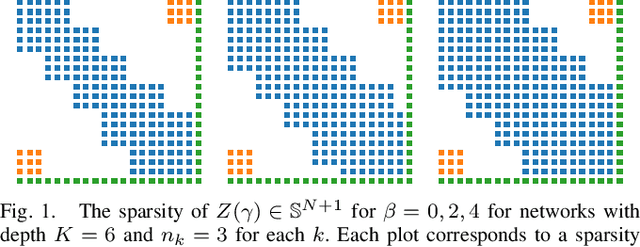
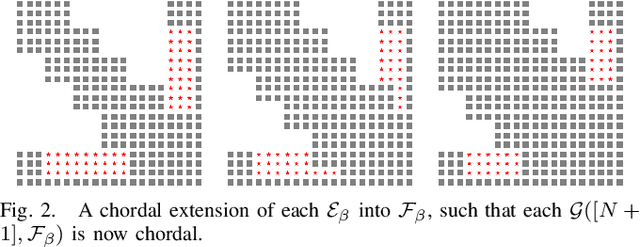
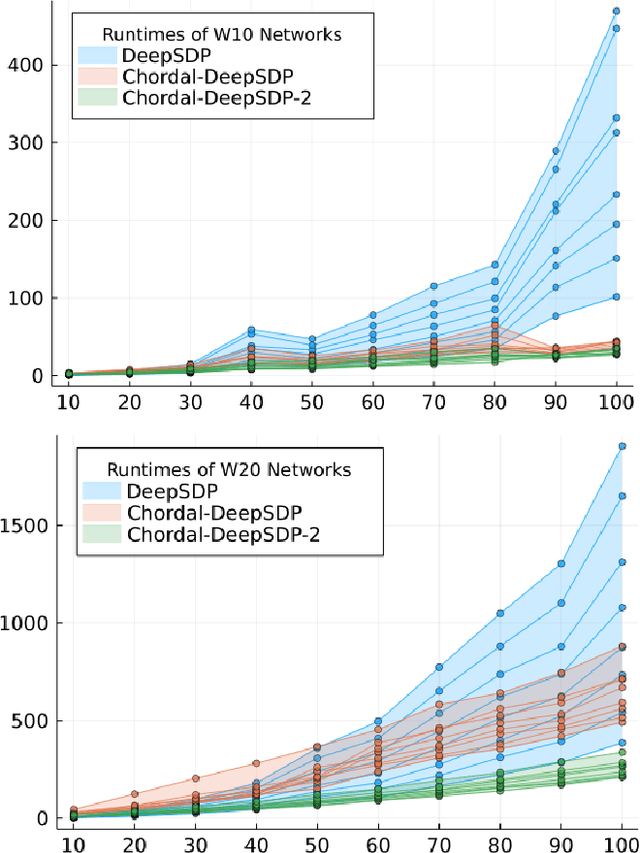
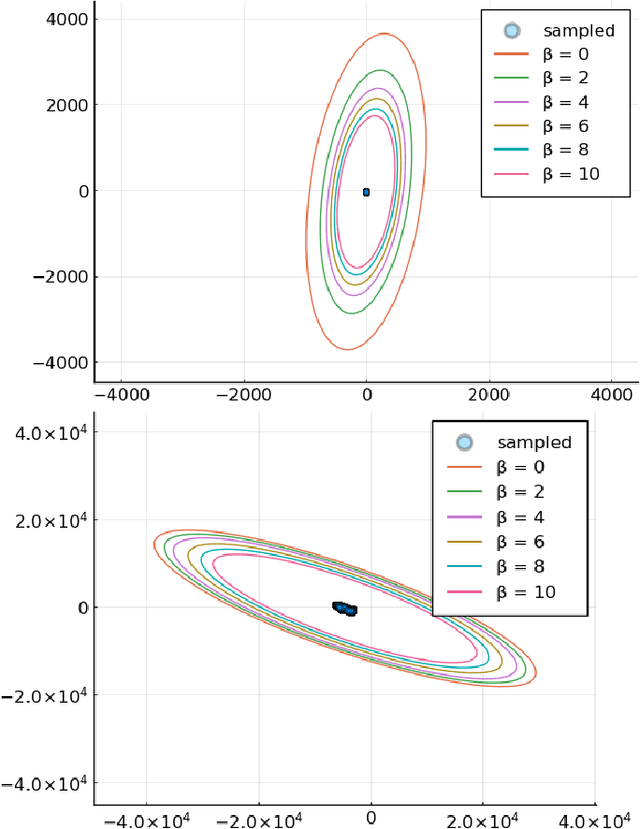
Many future technologies rely on neural networks, but verifying the correctness of their behavior remains a major challenge. It is known that neural networks can be fragile in the presence of even small input perturbations, yielding unpredictable outputs. The verification of neural networks is therefore vital to their adoption, and a number of approaches have been proposed in recent years. In this paper we focus on semidefinite programming (SDP) based techniques for neural network verification, which are particularly attractive because they can encode expressive behaviors while ensuring a polynomial time decision. Our starting point is the DeepSDP framework proposed by Fazlyab et al, which uses quadratic constraints to abstract the verification problem into a large-scale SDP. When the size of the neural network grows, however, solving this SDP quickly becomes intractable. Our key observation is that by leveraging chordal sparsity and specific parametrizations of DeepSDP, we can decompose the primary computational bottleneck of DeepSDP -- a large linear matrix inequality (LMI) -- into an equivalent collection of smaller LMIs. Our parametrization admits a tunable parameter, allowing us to trade-off efficiency and accuracy in the verification procedure. We call our formulation Chordal-DeepSDP, and provide experimental evaluation to show that it can: (1) effectively increase accuracy with the tunable parameter and (2) outperform DeepSDP on deeper networks.

Chordal Sparsity for Lipschitz Constant Estimation of Deep Neural Networks

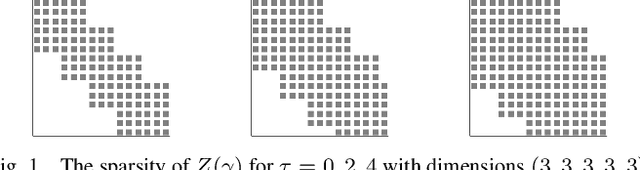
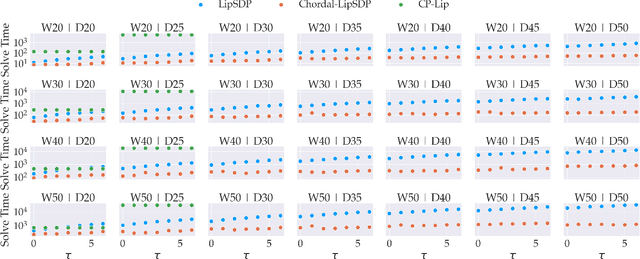
Lipschitz constants of neural networks allow for guarantees of robustness in image classification, safety in controller design, and generalizability beyond the training data. As calculating Lipschitz constants is NP-hard, techniques for estimating Lipschitz constants must navigate the trade-off between scalability and accuracy. In this work, we significantly push the scalability frontier of a semidefinite programming technique known as LipSDP while achieving zero accuracy loss. We first show that LipSDP has chordal sparsity, which allows us to derive a chordally sparse formulation that we call Chordal-LipSDP. The key benefit is that the main computational bottleneck of LipSDP, a large semidefinite constraint, is now decomposed into an equivalent collection of smaller ones: allowing Chordal-LipSDP to outperform LipSDP particularly as the network depth grows. Moreover, our formulation uses a tunable sparsity parameter that enables one to gain tighter estimates without incurring a significant computational cost. We illustrate the scalability of our approach through extensive numerical experiments.

Data-Driven System Level Synthesis

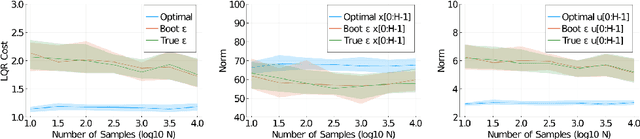
We establish data-driven versions of the System Level Synthesis (SLS) parameterization of stabilizing controllers for linear-time-invariant systems. Inspired by recent work in data-driven control that leverages tools from behavioral theory, we show that optimization problems over system-responses can be posed using only libraries of past system trajectories, without explicitly identifying a system model. We first consider the idealized setting of noise free trajectories, and show an exact equivalence between traditional and data-driven SLS. We then show that in the case of a system driven by process noise, tools from robust SLS can be used to characterize the effects of noise on closed-loop performance, and further draw on tools from matrix concentration to show that a simple trajectory averaging technique can be used to mitigate these effects. We end with numerical experiments showing the soundness of our methods.