Split Conformal Prediction in the Function Space with Neural Operators

Uncertainty quantification for neural operators remains an open problem in the infinite-dimensional setting due to the lack of finite-sample coverage guarantees over functional outputs. While conformal prediction offers finite-sample guarantees in finite-dimensional spaces, it does not directly extend to function-valued outputs. Existing approaches (Gaussian processes, Bayesian neural networks, and quantile-based operators) require strong distributional assumptions or yield conservative coverage. This work extends split conformal prediction to function spaces following a two step method. We first establish finite-sample coverage guarantees in a finite-dimensional space using a discretization map in the output function space. Then these guarantees are lifted to the function-space by considering the asymptotic convergence as the discretization is refined. To characterize the effect of resolution, we decompose the conformal radius into discretization, calibration, and misspecification components. This decomposition motivates a regression-based correction to transfer calibration across resolutions. Additionally, we propose two diagnostic metrics (conformal ensemble score and internal agreement) to quantify forecast degradation in autoregressive settings. Empirical results show that our method maintains calibrated coverage with less variation under resolution shifts and achieves better coverage in super-resolution tasks.

Multi-Agent Path Finding Among Dynamic Uncontrollable Agents with Statistical Safety Guarantees

Existing multi-agent path finding (MAPF) solvers do not account for uncertain behavior of uncontrollable agents. We present a novel variant of Enhanced Conflict-Based Search (ECBS), for both one-shot and lifelong MAPF in dynamic environments with uncontrollable agents. Our method consists of (1) training a learned predictor for the movement of uncontrollable agents, (2) quantifying the prediction error using conformal prediction (CP), a tool for statistical uncertainty quantification, and (3) integrating these uncertainty intervals into our modified ECBS solver. Our method can account for uncertain agent behavior, comes with statistical guarantees on collision-free paths for one-shot missions, and scales to lifelong missions with a receding horizon sequence of one-shot instances. We run our algorithm, CP-Solver, across warehouse and game maps, with competitive throughput and reduced collisions.

Deep Equivariant Multi-Agent Control Barrier Functions

With multi-agent systems increasingly deployed autonomously at scale in complex environments, ensuring safety of the data-driven policies is critical. Control Barrier Functions have emerged as an effective tool for enforcing safety constraints, yet existing learning-based methods often lack in scalability, generalization and sampling efficiency as they overlook inherent geometric structures of the system. To address this gap, we introduce symmetries-infused distributed Control Barrier Functions, enforcing the satisfaction of intrinsic symmetries on learnable graph-based safety certificates. We theoretically motivate the need for equivariant parametrization of CBFs and policies, and propose a simple, yet efficient and adaptable methodology for constructing such equivariant group-modular networks via the compatible group actions. This approach encodes safety constraints in a distributed data-efficient manner, enabling zero-shot generalization to larger and denser swarms. Through extensive simulations on multi-robot navigation tasks, we demonstrate that our method outperforms state-of-the-art baselines in terms of safety, scalability, and task success rates, highlighting the importance of embedding symmetries in safe distributed neural policies.

PCA-DDReach: Efficient Statistical Reachability Analysis of Stochastic Dynamical Systems via Principal Component Analysis

This study presents a scalable data-driven algorithm designed to efficiently address the challenging problem of reachability analysis. Analysis of cyber-physical systems (CPS) relies typically on parametric physical models of dynamical systems. However, identifying parametric physical models for complex CPS is challenging due to their complexity, uncertainty, and variability, often rendering them as black-box oracles. As an alternative, one can treat these complex systems as black-box models and use trajectory data sampled from the system (e.g., from high-fidelity simulators or the real system) along with machine learning techniques to learn models that approximate the underlying dynamics. However, these machine learning models can be inaccurate, highlighting the need for statistical tools to quantify errors. Recent advancements in the field include the incorporation of statistical uncertainty quantification tools such as conformal inference (CI) that can provide probabilistic reachable sets with provable guarantees. Recent work has even highlighted the ability of these tools to address the case where the distribution of trajectories sampled during training time are different from the distribution of trajectories encountered during deployment time. However, accounting for such distribution shifts typically results in more conservative guarantees. This is undesirable in practice and motivates us to present techniques that can reduce conservatism. Here, we propose a new approach that reduces conservatism and improves scalability by combining conformal inference with Principal Component Analysis (PCA). We show the effectiveness of our technique on various case studies, including a 12-dimensional quadcopter and a 27-dimensional hybrid system known as the powertrain.

Nonconvex Obstacle Avoidance using Efficient Sampling-Based Distance Functions

We consider nonconvex obstacle avoidance where a robot described by nonlinear dynamics and a nonconvex shape has to avoid nonconvex obstacles. Obstacle avoidance is a fundamental problem in robotics and well studied in control. However, existing solutions are computationally expensive (e.g., model predictive controllers), neglect nonlinear dynamics (e.g., graph-based planners), use diffeomorphic transformations into convex domains (e.g., for star shapes), or are conservative due to convex overapproximations. The key challenge here is that the computation of the distance between the shapes of the robot and the obstacles is a nonconvex problem. We propose efficient computation of this distance via sampling-based distance functions. We quantify the sampling error and show that, for certain systems, such sampling-based distance functions are valid nonsmooth control barrier functions. We also study how to deal with disturbances on the robot dynamics in our setting. Finally, we illustrate our method on a robot navigation task involving an omnidirectional robot and nonconvex obstacles. We also analyze performance and computational efficiency of our controller as a function of the number of samples.

Formal Verification and Control with Conformal Prediction

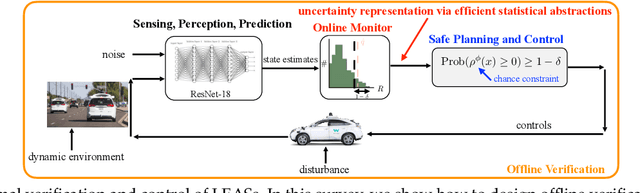
In this survey, we design formal verification and control algorithms for autonomous systems with practical safety guarantees using conformal prediction (CP), a statistical tool for uncertainty quantification. We focus on learning-enabled autonomous systems (LEASs) in which the complexity of learning-enabled components (LECs) is a major bottleneck that hampers the use of existing model-based verification and design techniques. Instead, we advocate for the use of CP, and we will demonstrate its use in formal verification, systems and control theory, and robotics. We argue that CP is specifically useful due to its simplicity (easy to understand, use, and modify), generality (requires no assumptions on learned models and data distributions, i.e., is distribution-free), and efficiency (real-time capable and accurate). We pursue the following goals with this survey. First, we provide an accessible introduction to CP for non-experts who are interested in using CP to solve problems in autonomy. Second, we show how to use CP for the verification of LECs, e.g., for verifying input-output properties of neural networks. Third and fourth, we review recent articles that use CP for safe control design as well as offline and online verification of LEASs. We summarize their ideas in a unifying framework that can deal with the complexity of LEASs in a computationally efficient manner. In our exposition, we consider simple system specifications, e.g., robot navigation tasks, as well as complex specifications formulated in temporal logic formalisms. Throughout our survey, we compare to other statistical techniques (e.g., scenario optimization, PAC-Bayes theory, etc.) and how these techniques have been used in verification and control. Lastly, we point the reader to open problems and future research directions.

Statistical Reachability Analysis of Stochastic Cyber-Physical Systems under Distribution Shift

Reachability analysis is a popular method to give safety guarantees for stochastic cyber-physical systems (SCPSs) that takes in a symbolic description of the system dynamics and uses set-propagation methods to compute an overapproximation of the set of reachable states over a bounded time horizon. In this paper, we investigate the problem of performing reachability analysis for an SCPS that does not have a symbolic description of the dynamics, but instead is described using a digital twin model that can be simulated to generate system trajectories. An important challenge is that the simulator implicitly models a probability distribution over the set of trajectories of the SCPS; however, it is typical to have a sim2real gap, i.e., the actual distribution of the trajectories in a deployment setting may be shifted from the distribution assumed by the simulator. We thus propose a statistical reachability analysis technique that, given a user-provided threshold $1-\epsilon$, provides a set that guarantees that any reachable state during deployment lies in this set with probability not smaller than this threshold. Our method is based on three main steps: (1) learning a deterministic surrogate model from sampled trajectories, (2) conducting reachability analysis over the surrogate model, and (3) employing {\em robust conformal inference} using an additional set of sampled trajectories to quantify the surrogate model's distribution shift with respect to the deployed SCPS. To counter conservatism in reachable sets, we propose a novel method to train surrogate models that minimizes a quantile loss term (instead of the usual mean squared loss), and a new method that provides tighter guarantees using conformal inference using a normalized surrogate error. We demonstrate the effectiveness of our technique on various case studies.

Recursively Feasible Shrinking-Horizon MPC in Dynamic Environments with Conformal Prediction Guarantees

In this paper, we focus on the problem of shrinking-horizon Model Predictive Control (MPC) in uncertain dynamic environments. We consider controlling a deterministic autonomous system that interacts with uncontrollable stochastic agents during its mission. Employing tools from conformal prediction, existing works derive high-confidence prediction regions for the unknown agent trajectories, and integrate these regions in the design of suitable safety constraints for MPC. Despite guaranteeing probabilistic safety of the closed-loop trajectories, these constraints do not ensure feasibility of the respective MPC schemes for the entire duration of the mission. We propose a shrinking-horizon MPC that guarantees recursive feasibility via a gradual relaxation of the safety constraints as new prediction regions become available online. This relaxation enforces the safety constraints to hold over the least restrictive prediction region from the set of all available prediction regions. In a comparative case study with the state of the art, we empirically show that our approach results in tighter prediction regions and verify recursive feasibility of our MPC scheme.

Reactive Temporal Logic-based Planning and Control for Interactive Robotic Tasks

Robots interacting with humans must be safe, reactive and adapt online to unforeseen environmental and task changes. Achieving these requirements concurrently is a challenge as interactive planners lack formal safety guarantees, while safe motion planners lack flexibility to adapt. To tackle this, we propose a modular control architecture that generates both safe and reactive motion plans for human-robot interaction by integrating temporal logic-based discrete task level plans with continuous Dynamical System (DS)-based motion plans. We formulate a reactive temporal logic formula that enables users to define task specifications through structured language, and propose a planning algorithm at the task level that generates a sequence of desired robot behaviors while being adaptive to environmental changes. At the motion level, we incorporate control Lyapunov functions and control barrier functions to compute stable and safe continuous motion plans for two types of robot behaviors: (i) complex, possibly periodic motions given by autonomous DS and (ii) time-critical tasks specified by Signal Temporal Logic~(STL). Our methodology is demonstrated on the Franka robot arm performing wiping tasks on a whiteboard and a mannequin that is compliant to human interactions and adaptive to environmental changes.

Robust STL Control Synthesis under Maximal Disturbance Sets

This work addresses maximally robust control synthesis under unknown disturbances. We consider a general nonlinear system, subject to a Signal Temporal Logic (STL) specification, and wish to jointly synthesize the maximal possible disturbance bounds and the corresponding controllers that ensure the STL specification is satisfied under these bounds. Many works have considered STL satisfaction under given bounded disturbances. Yet, to the authors' best knowledge, this is the first work that aims to maximize the permissible disturbance set and find the corresponding controllers that ensure satisfying the STL specification with maximum disturbance robustness. We extend the notion of disturbance-robust semantics for STL, which is a property of a specification, dynamical system, and controller, and provide an algorithm to get the maximal disturbance robust controllers satisfying an STL specification using Hamilton-Jacobi reachability. We show its soundness and provide a simulation example with an Autonomous Underwater Vehicle (AUV).