Jyotirmoy V. Deshmukh
When Environments Shift: Safe Planning with Generative Priors and Robust Conformal Prediction
Feb 13, 2026Abstract:Autonomous systems operate in environments that may change over time. An example is the control of a self-driving vehicle among pedestrians and human-controlled vehicles whose behavior may change based on factors such as traffic density, road visibility, and social norms. Therefore, the environment encountered during deployment rarely mirrors the environment and data encountered during training -- a phenomenon known as distribution shift -- which can undermine the safety of autonomous systems. Conformal prediction (CP) has recently been used along with data from the training environment to provide prediction regions that capture the behavior of the environment with a desired probability. When embedded within a model predictive controller (MPC), one can provide probabilistic safety guarantees, but only when the deployment and training environments coincide. Once a distribution shift occurs, these guarantees collapse. We propose a planning framework that is robust under distribution shifts by: (i) assuming that the underlying data distribution of the environment is parameterized by a nuisance parameter, i.e., an observable, interpretable quantity such as traffic density, (ii) training a conditional diffusion model that captures distribution shifts as a function of the nuisance parameter, (iii) observing the nuisance parameter online and generating cheap, synthetic data from the diffusion model for the observed nuisance parameter, and (iv) designing an MPC that embeds CP regions constructed from such synthetic data. Importantly, we account for discrepancies between the underlying data distribution and the diffusion model by using robust CP. Thus, the plans computed using robust CP enjoy probabilistic safety guarantees, in contrast with plans obtained from a single, static set of training data. We empirically demonstrate safety under diverse distribution shifts in the ORCA simulator.
Multi-Agent Path Finding via Offline RL and LLM Collaboration
Sep 26, 2025Abstract:Multi-Agent Path Finding (MAPF) poses a significant and challenging problem critical for applications in robotics and logistics, particularly due to its combinatorial complexity and the partial observability inherent in realistic environments. Decentralized reinforcement learning methods commonly encounter two substantial difficulties: first, they often yield self-centered behaviors among agents, resulting in frequent collisions, and second, their reliance on complex communication modules leads to prolonged training times, sometimes spanning weeks. To address these challenges, we propose an efficient decentralized planning framework based on the Decision Transformer (DT), uniquely leveraging offline reinforcement learning to substantially reduce training durations from weeks to mere hours. Crucially, our approach effectively handles long-horizon credit assignment and significantly improves performance in scenarios with sparse and delayed rewards. Furthermore, to overcome adaptability limitations inherent in standard RL methods under dynamic environmental changes, we integrate a large language model (GPT-4o) to dynamically guide agent policies. Extensive experiments in both static and dynamically changing environments demonstrate that our DT-based approach, augmented briefly by GPT-4o, significantly enhances adaptability and performance.
ConformalNL2LTL: Translating Natural Language Instructions into Temporal Logic Formulas with Conformal Correctness Guarantees
Apr 22, 2025Abstract:Linear Temporal Logic (LTL) has become a prevalent specification language for robotic tasks. To mitigate the significant manual effort and expertise required to define LTL-encoded tasks, several methods have been proposed for translating Natural Language (NL) instructions into LTL formulas, which, however, lack correctness guarantees. To address this, we introduce a new NL-to-LTL translation method, called ConformalNL2LTL, that can achieve user-defined translation success rates over unseen NL commands. Our method constructs LTL formulas iteratively by addressing a sequence of open-vocabulary Question-Answering (QA) problems with LLMs. To enable uncertainty-aware translation, we leverage conformal prediction (CP), a distribution-free uncertainty quantification tool for black-box models. CP enables our method to assess the uncertainty in LLM-generated answers, allowing it to proceed with translation when sufficiently confident and request help otherwise. We provide both theoretical and empirical results demonstrating that ConformalNL2LTL achieves user-specified translation accuracy while minimizing help rates.
Coordinating Spinal and Limb Dynamics for Enhanced Sprawling Robot Mobility
Apr 18, 2025

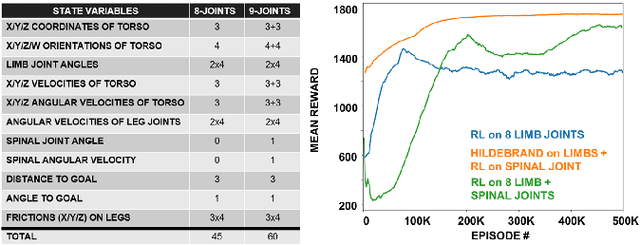
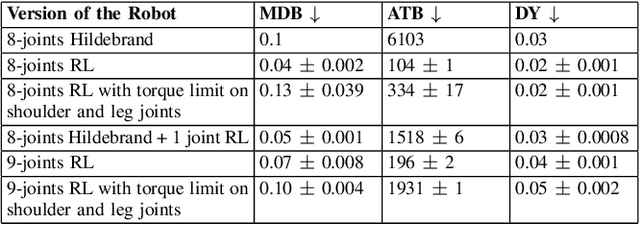
Abstract:Among vertebrates, salamanders, with their unique ability to transition between walking and swimming gaits, highlight the role of spinal mobility in locomotion. A flexible spine enables undulation of the body through a wavelike motion along the spine, aiding navigation over uneven terrains and obstacles. Yet environmental uncertainties, such as surface irregularities and variations in friction, can significantly disrupt body-limb coordination and cause discrepancies between predictions from mathematical models and real-world outcomes. Addressing this challenge requires the development of sophisticated control strategies capable of dynamically adapting to uncertain conditions while maintaining efficient locomotion. Deep reinforcement learning (DRL) offers a promising framework for handling non-deterministic environments and enabling robotic systems to adapt effectively and perform robustly under challenging conditions. In this study, we comparatively examine learning-based control strategies and biologically inspired gait design methods on a salamander-like robot.
Multi-agent Path Finding for Timed Tasks using Evolutionary Games
Nov 15, 2024Abstract:Autonomous multi-agent systems such as hospital robots and package delivery drones often operate in highly uncertain environments and are expected to achieve complex temporal task objectives while ensuring safety. While learning-based methods such as reinforcement learning are popular methods to train single and multi-agent autonomous systems under user-specified and state-based reward functions, applying these methods to satisfy trajectory-level task objectives is a challenging problem. Our first contribution is the use of weighted automata to specify trajectory-level objectives, such that, maximal paths induced in the weighted automaton correspond to desired trajectory-level behaviors. We show how weighted automata-based specifications go beyond timeliness properties focused on deadlines to performance properties such as expeditiousness. Our second contribution is the use of evolutionary game theory (EGT) principles to train homogeneous multi-agent teams targeting homogeneous task objectives. We show how shared experiences of agents and EGT-based policy updates allow us to outperform state-of-the-art reinforcement learning (RL) methods in minimizing path length by nearly 30\% in large spaces. We also show that our algorithm is computationally faster than deep RL methods by at least an order of magnitude. Additionally our results indicate that it scales better with an increase in the number of agents as compared to other methods.
Motion Planning for Automata-based Objectives using Efficient Gradient-based Methods
Oct 15, 2024



Abstract:In recent years, there has been increasing interest in using formal methods-based techniques to safely achieve temporal tasks, such as timed sequence of goals, or patrolling objectives. Such tasks are often expressed in real-time logics such as Signal Temporal Logic (STL), whereby, the logical specification is encoded into an optimization problem. Such approaches usually involve optimizing over the quantitative semantics, or robustness degree, of the logic over bounded horizons: the semantics can be encoded as mixed-integer linear constraints or into smooth approximations of the robustness degree. A major limitation of this approach is that it faces scalability challenges with respect to temporal complexity: for example, encoding long-term tasks requires storing the entire history of the system. In this paper, we present a quantitative generalization of such tasks in the form of symbolic automata objectives. Specifically, we show that symbolic automata can be expressed as matrix operators that lend themselves to automatic differentiation, allowing for the use of off-the-shelf gradient-based optimizers. We show how this helps solve the need to store arbitrarily long system trajectories, while efficiently leveraging the task structure encoded in the automaton.
Formal Verification and Control with Conformal Prediction
Aug 31, 2024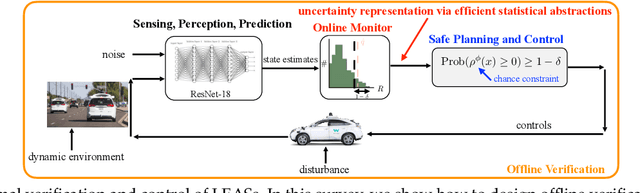
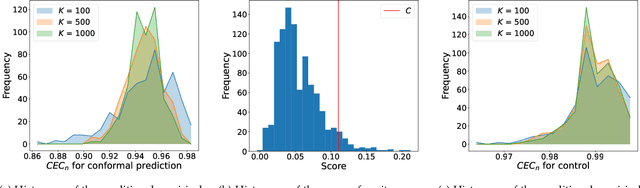
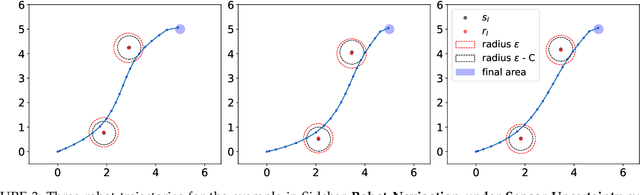
Abstract:In this survey, we design formal verification and control algorithms for autonomous systems with practical safety guarantees using conformal prediction (CP), a statistical tool for uncertainty quantification. We focus on learning-enabled autonomous systems (LEASs) in which the complexity of learning-enabled components (LECs) is a major bottleneck that hampers the use of existing model-based verification and design techniques. Instead, we advocate for the use of CP, and we will demonstrate its use in formal verification, systems and control theory, and robotics. We argue that CP is specifically useful due to its simplicity (easy to understand, use, and modify), generality (requires no assumptions on learned models and data distributions, i.e., is distribution-free), and efficiency (real-time capable and accurate). We pursue the following goals with this survey. First, we provide an accessible introduction to CP for non-experts who are interested in using CP to solve problems in autonomy. Second, we show how to use CP for the verification of LECs, e.g., for verifying input-output properties of neural networks. Third and fourth, we review recent articles that use CP for safe control design as well as offline and online verification of LEASs. We summarize their ideas in a unifying framework that can deal with the complexity of LEASs in a computationally efficient manner. In our exposition, we consider simple system specifications, e.g., robot navigation tasks, as well as complex specifications formulated in temporal logic formalisms. Throughout our survey, we compare to other statistical techniques (e.g., scenario optimization, PAC-Bayes theory, etc.) and how these techniques have been used in verification and control. Lastly, we point the reader to open problems and future research directions.
Statistical Reachability Analysis of Stochastic Cyber-Physical Systems under Distribution Shift
Jul 16, 2024



Abstract:Reachability analysis is a popular method to give safety guarantees for stochastic cyber-physical systems (SCPSs) that takes in a symbolic description of the system dynamics and uses set-propagation methods to compute an overapproximation of the set of reachable states over a bounded time horizon. In this paper, we investigate the problem of performing reachability analysis for an SCPS that does not have a symbolic description of the dynamics, but instead is described using a digital twin model that can be simulated to generate system trajectories. An important challenge is that the simulator implicitly models a probability distribution over the set of trajectories of the SCPS; however, it is typical to have a sim2real gap, i.e., the actual distribution of the trajectories in a deployment setting may be shifted from the distribution assumed by the simulator. We thus propose a statistical reachability analysis technique that, given a user-provided threshold $1-\epsilon$, provides a set that guarantees that any reachable state during deployment lies in this set with probability not smaller than this threshold. Our method is based on three main steps: (1) learning a deterministic surrogate model from sampled trajectories, (2) conducting reachability analysis over the surrogate model, and (3) employing {\em robust conformal inference} using an additional set of sampled trajectories to quantify the surrogate model's distribution shift with respect to the deployed SCPS. To counter conservatism in reachable sets, we propose a novel method to train surrogate models that minimizes a quantile loss term (instead of the usual mean squared loss), and a new method that provides tighter guarantees using conformal inference using a normalized surrogate error. We demonstrate the effectiveness of our technique on various case studies.
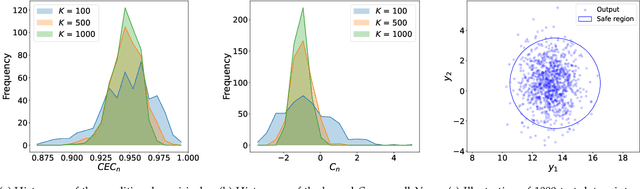
Conformal Predictive Programming for Chance Constrained Optimization
Feb 12, 2024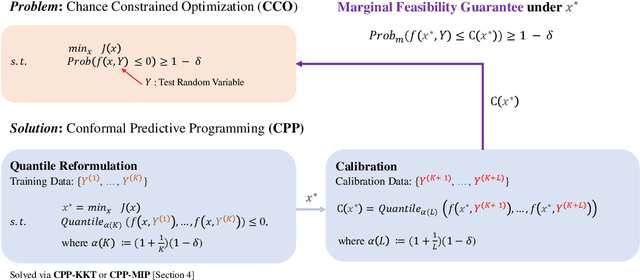


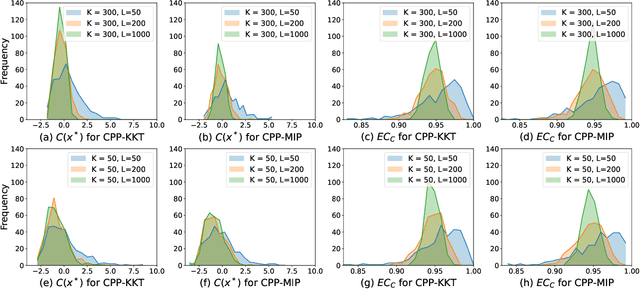
Abstract:Motivated by the advances in conformal prediction (CP), we propose conformal predictive programming (CPP), an approach to solve chance constrained optimization (CCO) problems, i.e., optimization problems with nonlinear constraint functions affected by arbitrary random parameters. CPP utilizes samples from these random parameters along with the quantile lemma -- which is central to CP -- to transform the CCO problem into a deterministic optimization problem. We then present two tractable reformulations of CPP by: (1) writing the quantile as a linear program along with its KKT conditions (CPP-KKT), and (2) using mixed integer programming (CPP-MIP). CPP comes with marginal probabilistic feasibility guarantees for the CCO problem that are conceptually different from existing approaches, e.g., the sample approximation and the scenario approach. While we explore algorithmic similarities with the sample approximation approach, we emphasize that the strength of CPP is that it can easily be extended to incorporate different variants of CP. To illustrate this, we present robust conformal predictive programming to deal with distribution shifts in the uncertain parameters of the CCO problem.
Robust Conformal Prediction for STL Runtime Verification under Distribution Shift
Nov 16, 2023



Abstract:Cyber-physical systems (CPS) designed in simulators behave differently in the real-world. Once they are deployed in the real-world, we would hence like to predict system failures during runtime. We propose robust predictive runtime verification (RPRV) algorithms under signal temporal logic (STL) tasks for general stochastic CPS. The RPRV problem faces several challenges: (1) there may not be sufficient data of the behavior of the deployed CPS, (2) predictive models are based on a distribution over system trajectories encountered during the design phase, i.e., there may be a distribution shift during deployment. To address these challenges, we assume to know an upper bound on the statistical distance (in terms of an f-divergence) between the distributions at deployment and design time, and we utilize techniques based on robust conformal prediction. Motivated by our results in [1], we construct an accurate and an interpretable RPRV algorithm. We use a trajectory prediction model to estimate the system behavior at runtime and robust conformal prediction to obtain probabilistic guarantees by accounting for distribution shifts. We precisely quantify the relationship between calibration data, desired confidence, and permissible distribution shift. To the best of our knowledge, these are the first statistically valid algorithms under distribution shift in this setting. We empirically validate our algorithms on a Franka manipulator within the NVIDIA Isaac sim environment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge