Multi-Agent Path Finding via Offline RL and LLM Collaboration

Multi-Agent Path Finding (MAPF) poses a significant and challenging problem critical for applications in robotics and logistics, particularly due to its combinatorial complexity and the partial observability inherent in realistic environments. Decentralized reinforcement learning methods commonly encounter two substantial difficulties: first, they often yield self-centered behaviors among agents, resulting in frequent collisions, and second, their reliance on complex communication modules leads to prolonged training times, sometimes spanning weeks. To address these challenges, we propose an efficient decentralized planning framework based on the Decision Transformer (DT), uniquely leveraging offline reinforcement learning to substantially reduce training durations from weeks to mere hours. Crucially, our approach effectively handles long-horizon credit assignment and significantly improves performance in scenarios with sparse and delayed rewards. Furthermore, to overcome adaptability limitations inherent in standard RL methods under dynamic environmental changes, we integrate a large language model (GPT-4o) to dynamically guide agent policies. Extensive experiments in both static and dynamically changing environments demonstrate that our DT-based approach, augmented briefly by GPT-4o, significantly enhances adaptability and performance.

Coordinating Spinal and Limb Dynamics for Enhanced Sprawling Robot Mobility

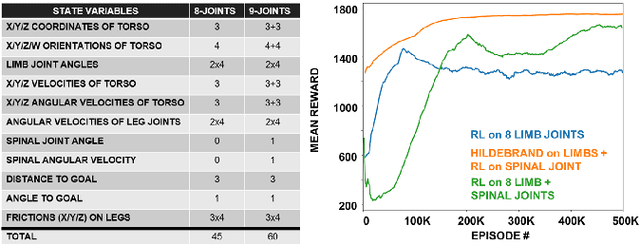
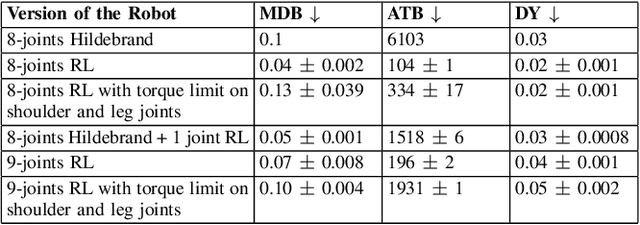
Among vertebrates, salamanders, with their unique ability to transition between walking and swimming gaits, highlight the role of spinal mobility in locomotion. A flexible spine enables undulation of the body through a wavelike motion along the spine, aiding navigation over uneven terrains and obstacles. Yet environmental uncertainties, such as surface irregularities and variations in friction, can significantly disrupt body-limb coordination and cause discrepancies between predictions from mathematical models and real-world outcomes. Addressing this challenge requires the development of sophisticated control strategies capable of dynamically adapting to uncertain conditions while maintaining efficient locomotion. Deep reinforcement learning (DRL) offers a promising framework for handling non-deterministic environments and enabling robotic systems to adapt effectively and perform robustly under challenging conditions. In this study, we comparatively examine learning-based control strategies and biologically inspired gait design methods on a salamander-like robot.

Motion Planning for Automata-based Objectives using Efficient Gradient-based Methods

In recent years, there has been increasing interest in using formal methods-based techniques to safely achieve temporal tasks, such as timed sequence of goals, or patrolling objectives. Such tasks are often expressed in real-time logics such as Signal Temporal Logic (STL), whereby, the logical specification is encoded into an optimization problem. Such approaches usually involve optimizing over the quantitative semantics, or robustness degree, of the logic over bounded horizons: the semantics can be encoded as mixed-integer linear constraints or into smooth approximations of the robustness degree. A major limitation of this approach is that it faces scalability challenges with respect to temporal complexity: for example, encoding long-term tasks requires storing the entire history of the system. In this paper, we present a quantitative generalization of such tasks in the form of symbolic automata objectives. Specifically, we show that symbolic automata can be expressed as matrix operators that lend themselves to automatic differentiation, allowing for the use of off-the-shelf gradient-based optimizers. We show how this helps solve the need to store arbitrarily long system trajectories, while efficiently leveraging the task structure encoded in the automaton.