Formal Verification and Control with Conformal Prediction

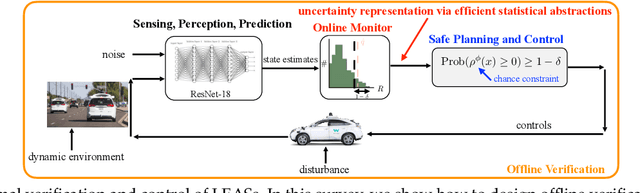
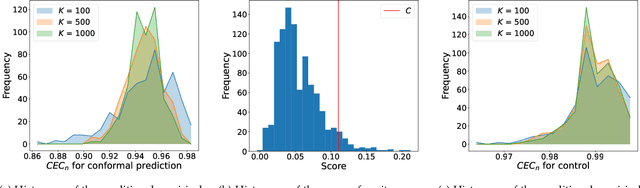
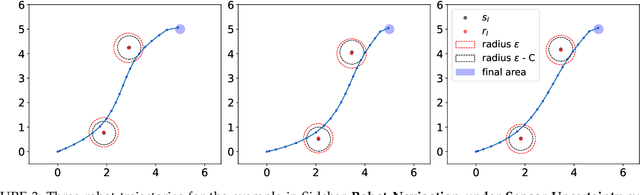
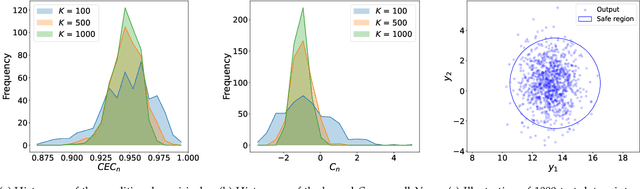
In this survey, we design formal verification and control algorithms for autonomous systems with practical safety guarantees using conformal prediction (CP), a statistical tool for uncertainty quantification. We focus on learning-enabled autonomous systems (LEASs) in which the complexity of learning-enabled components (LECs) is a major bottleneck that hampers the use of existing model-based verification and design techniques. Instead, we advocate for the use of CP, and we will demonstrate its use in formal verification, systems and control theory, and robotics. We argue that CP is specifically useful due to its simplicity (easy to understand, use, and modify), generality (requires no assumptions on learned models and data distributions, i.e., is distribution-free), and efficiency (real-time capable and accurate). We pursue the following goals with this survey. First, we provide an accessible introduction to CP for non-experts who are interested in using CP to solve problems in autonomy. Second, we show how to use CP for the verification of LECs, e.g., for verifying input-output properties of neural networks. Third and fourth, we review recent articles that use CP for safe control design as well as offline and online verification of LEASs. We summarize their ideas in a unifying framework that can deal with the complexity of LEASs in a computationally efficient manner. In our exposition, we consider simple system specifications, e.g., robot navigation tasks, as well as complex specifications formulated in temporal logic formalisms. Throughout our survey, we compare to other statistical techniques (e.g., scenario optimization, PAC-Bayes theory, etc.) and how these techniques have been used in verification and control. Lastly, we point the reader to open problems and future research directions.