Parameter-Robust MPPI for Safe Online Learning of Unknown Parameters

Robots deployed in dynamic environments must remain safe even when key physical parameters are uncertain or change over time. We propose Parameter-Robust Model Predictive Path Integral (PRMPPI) control, a framework that integrates online parameter learning with probabilistic safety constraints. PRMPPI maintains a particle-based belief over parameters via Stein Variational Gradient Descent, evaluates safety constraints using Conformal Prediction, and optimizes both a nominal performance-driven and a safety-focused backup trajectory in parallel. This yields a controller that is cautious at first, improves performance as parameters are learned, and ensures safety throughout. Simulation and hardware experiments demonstrate higher success rates, lower tracking error, and more accurate parameter estimates than baselines.

Exact Smooth Reformulations for Trajectory Optimization Under Signal Temporal Logic Specifications

We study motion planning under Signal Temporal Logic (STL), a useful formalism for specifying spatial-temporal requirements. We pose STL synthesis as a trajectory optimization problem leveraging the STL robustness semantics. To obtain a differentiable problem without approximation error, we introduce an exact reformulation of the max and min operators. The resulting method is exact, smooth, and sound. We validate it in numerical simulations, demonstrating its practical performance.

BURNS: Backward Underapproximate Reachability for Neural-Feedback-Loop Systems

Learning-enabled planning and control algorithms are increasingly popular, but they often lack rigorous guarantees of performance or safety. We introduce an algorithm for computing underapproximate backward reachable sets of nonlinear discrete time neural feedback loops. We then use the backward reachable sets to check goal-reaching properties. Our algorithm is based on overapproximating the system dynamics function to enable computation of underapproximate backward reachable sets through solutions of mixed-integer linear programs. We rigorously analyze the soundness of our algorithm and demonstrate it on a numerical example. Our work expands the class of properties that can be verified for learning-enabled systems.

Collaborative Object Transportation in Space via Impact Interactions

We present a planning and control approach for collaborative transportation of objects in space by a team of robots. Object and robots in microgravity environments are not subject to friction but are instead free floating. This property is key to how we approach the transportation problem: the passive objects are controlled by impact interactions with the controlled robots. In particular, given a high-level Signal Temporal Logic (STL) specification of the transportation task, we synthesize motion plans for the robots to maximize the specification satisfaction in terms of spatial STL robustness. Given that the physical impact interactions are complex and hard to model precisely, we also present an alternative formulation maximizing the permissible uncertainty in a simplified kinematic impact model. We define the full planning and control stack required to solve the object transportation problem; an offline planner, an online replanner, and a low-level model-predictive control scheme for each of the robots. We show the method in a high-fidelity simulator for a variety of scenarios and present experimental validation of 2-robot, 1-object scenarios on a freeflyer platform.

Risk-Aware Robot Control in Dynamic Environments Using Belief Control Barrier Functions

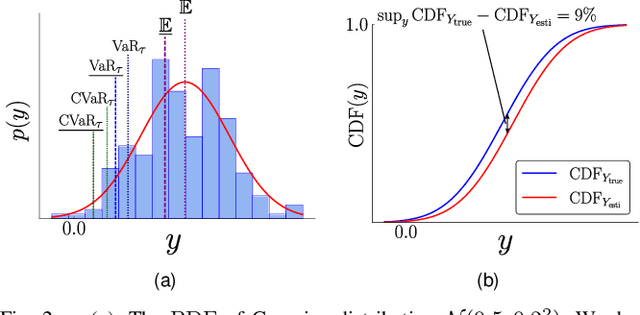
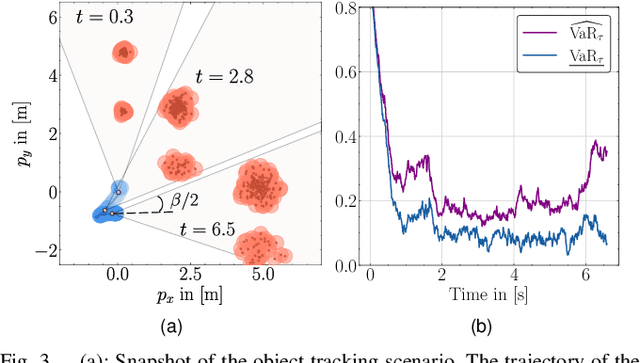
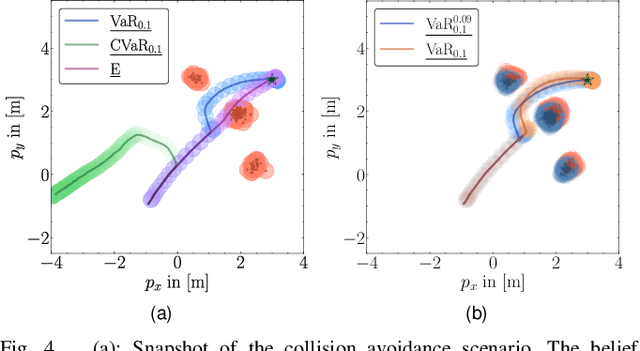
Ensuring safety for autonomous robots operating in dynamic environments can be challenging due to factors such as unmodeled dynamics, noisy sensor measurements, and partial observability. To account for these limitations, it is common to maintain a belief distribution over the true state. This belief could be a non-parametric, sample-based representation to capture uncertainty more flexibly. In this paper, we propose a novel form of Belief Control Barrier Functions (BCBFs) specifically designed to ensure safety in dynamic environments under stochastic dynamics and a sample-based belief about the environment state. Our approach incorporates provable concentration bounds on tail risk measures into BCBFs, effectively addressing possible multimodal and skewed belief distributions represented by samples. Moreover, the proposed method demonstrates robustness against distributional shifts up to a predefined bound. We validate the effectiveness and real-time performance (approximately 1kHz) of the proposed method through two simulated underwater robotic applications: object tracking and dynamic collision avoidance.

Pedestrian-Aware Motion Planning for Autonomous Driving in Complex Urban Scenarios

Motion planning in uncertain environments like complex urban areas is a key challenge for autonomous vehicles (AVs). The aim of our research is to investigate how AVs can navigate crowded, unpredictable scenarios with multiple pedestrians while maintaining a safe and efficient vehicle behavior. So far, most research has concentrated on static or deterministic traffic participant behavior. This paper introduces a novel algorithm for motion planning in crowded spaces by combining social force principles for simulating realistic pedestrian behavior with a risk-aware motion planner. We evaluate this new algorithm in a 2D simulation environment to rigorously assess AV-pedestrian interactions, demonstrating that our algorithm enables safe, efficient, and adaptive motion planning, particularly in highly crowded urban environments - a first in achieving this level of performance. This study has not taken into consideration real-time constraints and has been shown only in simulation so far. Further studies are needed to investigate the novel algorithm in a complete software stack for AVs on real cars to investigate the entire perception, planning and control pipeline in crowded scenarios. We release the code developed in this research as an open-source resource for further studies and development. It can be accessed at the following link: https://github.com/TUM-AVS/PedestrianAwareMotionPlanning

Towards Open-Source and Modular Space Systems with ATMOS

In the near future, autonomous space systems will compose a large number of the spacecraft being deployed. Their tasks will involve autonomous rendezvous and proximity operations with large structures, such as inspections or assembly of orbiting space stations and maintenance and human-assistance tasks over shared workspaces. To promote replicable and reliable scientific results for autonomous control of spacecraft, we present the design of a space systems laboratory based on open-source and modular software and hardware. The simulation software provides a software-in-the-loop (SITL) architecture that seamlessly transfers simulated results to the ATMOS platforms, developed for testing of multi-agent autonomy schemes for microgravity. The manuscript presents the KTH space systems laboratory facilities and the ATMOS platform as open-source hardware and software contributions. Preliminary results showcase SITL and real testing.

Efficient Non-Myopic Layered Bayesian Optimization For Large-Scale Bathymetric Informative Path Planning

Informative path planning (IPP) applied to bathymetric mapping allows AUVs to focus on feature-rich areas to quickly reduce uncertainty and increase mapping efficiency. Existing methods based on Bayesian optimization (BO) over Gaussian Process (GP) maps work well on small scenarios but they are short-sighted and computationally heavy when mapping larger areas, hindering deployment in real applications. To overcome this, we present a 2-layered BO IPP method that performs non-myopic, real-time planning in a tree search fashion over large Stochastic Variational GP maps, while respecting the AUV motion constraints and accounting for localization uncertainty. Our framework outperforms the standard industrial lawn-mowing pattern and a myopic baseline in a set of hardware in the loop (HIL) experiments in an embedded platform over real bathymetry.

Co-Designing Tools and Control Policies for Robust Manipulation

Inherent robustness in manipulation is prevalent in biological systems and critical for robotic manipulation systems due to real-world uncertainties and disturbances. This robustness relies not only on robust control policies but also on the design characteristics of the end-effectors. This paper introduces a bi-level optimization approach to co-designing tools and control policies to achieve robust manipulation. The approach employs reinforcement learning for lower-level control policy learning and multi-task Bayesian optimization for upper-level design optimization. Diverging from prior approaches, we incorporate caging-based robustness metrics into both levels, ensuring manipulation robustness against disturbances and environmental variations. Our method is evaluated in four non-prehensile manipulation environments, demonstrating improvements in task success rate under disturbances and environment changes. A real-world experiment is also conducted to validate the framework's practical effectiveness.

TTT: A Temporal Refinement Heuristic for Tenuously Tractable Discrete Time Reachability Problems

Reachable set computation is an important tool for analyzing control systems. Simulating a control system can show that the system is generally functioning as desired, but a formal tool like reachability analysis can provide a guarantee of correctness. For linear systems, reachability analysis is straightforward and fast, but as more complex components are added to the control system such as nonlinear dynamics or a neural network controller, reachability analysis may slow down or become overly conservative. To address these challenges, much literature has focused on spatial refinement, e.g., tuning the discretization of the input sets and intermediate reachable sets. However, this paper addresses a different dimension: temporal refinement. The basic idea of temporal refinement is to automatically choose when along the horizon of the reachability problem to execute slow symbolic queries which incur less approximation error versus fast concrete queries which incur more approximation error. Temporal refinement can be combined with other refinement approaches and offers an additional ``tuning knob'' with which to trade off tractability and tightness in approximate reachable set computation. Here, we introduce an automatic framework for performing temporal refinement and we demonstrate the effectiveness of this technique on computing approximate reachable sets for nonlinear systems with neural network control policies. We demonstrate the calculation of reachable sets of varying approximation error under varying computational budget and show that our algorithm is able to generate approximate reachable sets with a similar amount of error to the baseline approach in 20-70% less time.