Risk-Aware Robot Control in Dynamic Environments Using Belief Control Barrier Functions

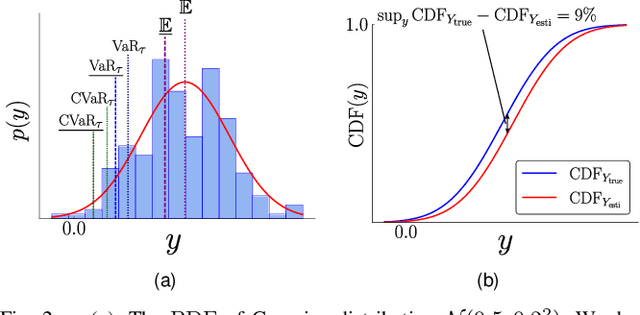
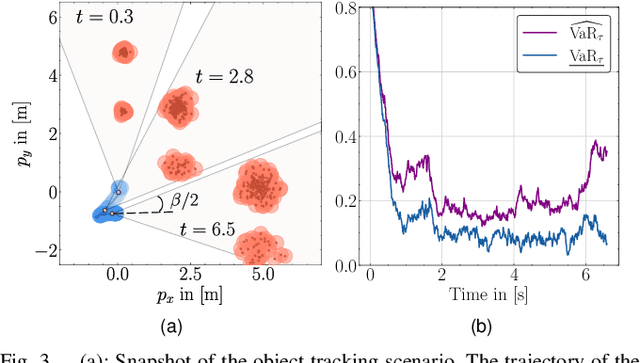
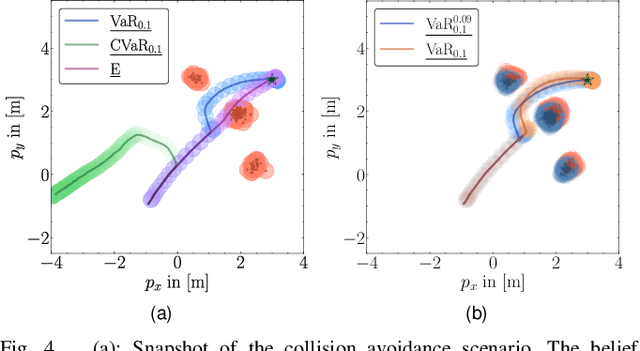
Ensuring safety for autonomous robots operating in dynamic environments can be challenging due to factors such as unmodeled dynamics, noisy sensor measurements, and partial observability. To account for these limitations, it is common to maintain a belief distribution over the true state. This belief could be a non-parametric, sample-based representation to capture uncertainty more flexibly. In this paper, we propose a novel form of Belief Control Barrier Functions (BCBFs) specifically designed to ensure safety in dynamic environments under stochastic dynamics and a sample-based belief about the environment state. Our approach incorporates provable concentration bounds on tail risk measures into BCBFs, effectively addressing possible multimodal and skewed belief distributions represented by samples. Moreover, the proposed method demonstrates robustness against distributional shifts up to a predefined bound. We validate the effectiveness and real-time performance (approximately 1kHz) of the proposed method through two simulated underwater robotic applications: object tracking and dynamic collision avoidance.

Forward Invariance in Trajectory Spaces for Safety-critical Control

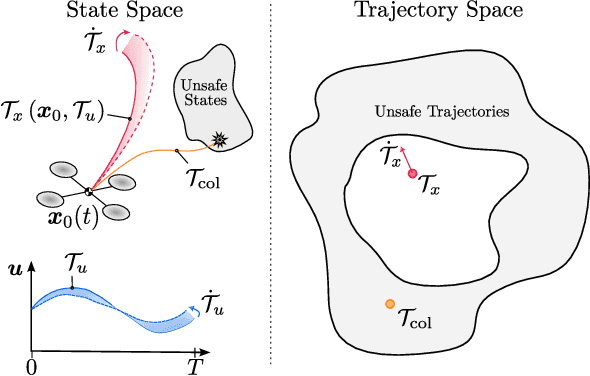
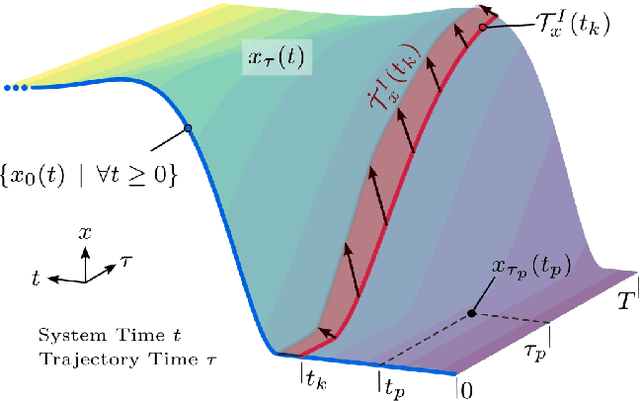
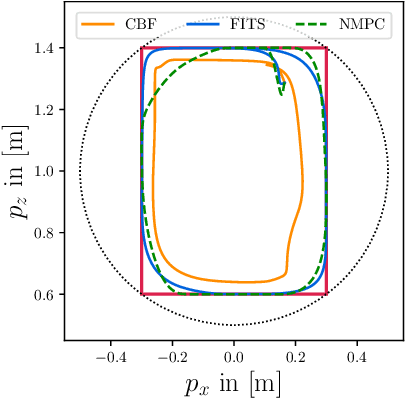
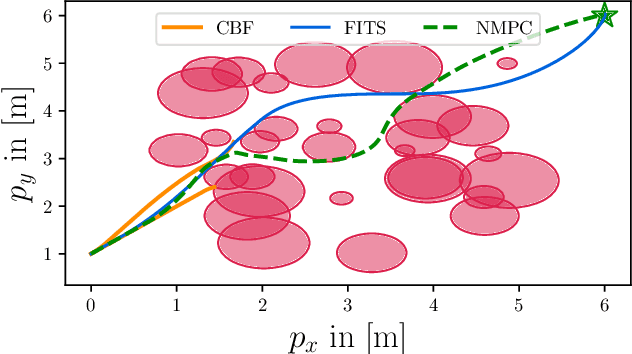
Useful robot control algorithms should not only achieve performance objectives but also adhere to hard safety constraints. Control Barrier Functions (CBFs) have been developed to provably ensure system safety through forward invariance. However, they often unnecessarily sacrifice performance for safety since they are purely reactive. Receding horizon control (RHC), on the other hand, consider planned trajectories to account for the future evolution of a system. This work provides a new perspective on safety-critical control by introducing Forward Invariance in Trajectory Spaces (FITS). We lift the problem of safe RHC into the trajectory space and describe the evolution of planned trajectories as a controlled dynamical system. Safety constraints defined over states can be converted into sets in the trajectory space which we render forward invariant via a CBF framework. We derive an efficient quadratic program (QP) to synthesize trajectories that provably satisfy safety constraints. Our experiments support that FITS improves the adherence to safety specifications without sacrificing performance over alternative CBF and NMPC methods.

Risk-aware Control for Robots with Non-Gaussian Belief Spaces

This paper addresses the problem of safety-critical control of autonomous robots, considering the ubiquitous uncertainties arising from unmodeled dynamics and noisy sensors. To take into account these uncertainties, probabilistic state estimators are often deployed to obtain a belief over possible states. Namely, Particle Filters (PFs) can handle arbitrary non-Gaussian distributions in the robot's state. In this work, we define the belief state and belief dynamics for continuous-discrete PFs and construct safe sets in the underlying belief space. We design a controller that provably keeps the robot's belief state within this safe set. As a result, we ensure that the risk of the unknown robot's state violating a safety specification, such as avoiding a dangerous area, is bounded. We provide an open-source implementation as a ROS2 package and evaluate the solution in simulations and hardware experiments involving high-dimensional belief spaces.

Non-smooth Control Barrier Functions for Stochastic Dynamical Systems

Uncertainties arising in various control systems, such as robots that are subject to unknown disturbances or environmental variations, pose significant challenges for ensuring system safety, such as collision avoidance. At the same time, safety specifications are getting more and more complex, e.g., by composing multiple safety objectives through Boolean operators resulting in non-smooth descriptions of safe sets. Control Barrier Functions (CBFs) have emerged as a control technique to provably guarantee system safety. In most settings, they rely on an assumption of having deterministic dynamics and smooth safe sets. This paper relaxes these two assumptions by extending CBFs to encompass control systems with stochastic dynamics and safe sets defined by non-smooth functions. By explicitly considering the stochastic nature of system dynamics and accommodating complex safety specifications, our method enables the design of safe control strategies in uncertain and complex systems. We provide formal guarantees on the safety of the system by leveraging the theoretical foundations of stochastic CBFs and non-smooth safe sets. Numerical simulations demonstrate the effectiveness of the approach in various scenarios.

Belief Control Barrier Functions for Risk-aware Control

Ensuring safety in real-world robotic systems is often challenging due to unmodeled disturbances and noisy sensor measurements. To account for such stochastic uncertainties, many robotic systems leverage probabilistic state estimators such as Kalman filters to obtain a robot's belief, i.e. a probability distribution over possible states. We propose belief control barrier functions (BCBFs) to enable risk-aware control synthesis, leveraging all information provided by state estimators. This allows robots to stay in predefined safety regions with desired confidence under these stochastic uncertainties. BCBFs are general and can be applied to a variety of robotic systems that use extended Kalman filters as state estimator. We demonstrate BCBFs on a quadrotor that is exposed to external disturbances and varying sensing conditions. Our results show improved safety compared to traditional state-based approaches while allowing control frequencies of up to 1kHz.