Chelsea Sidrane
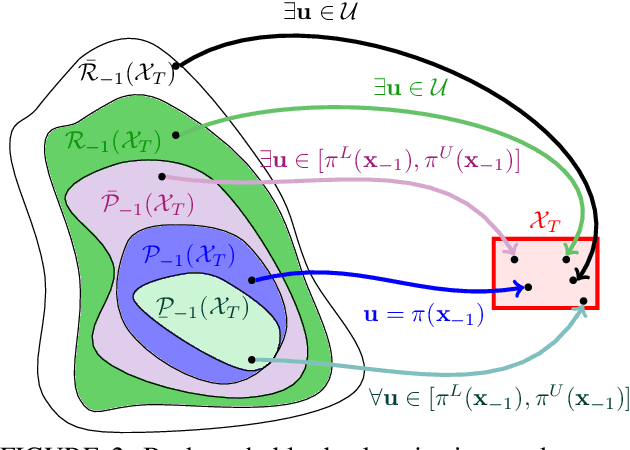
BURNS: Backward Underapproximate Reachability for Neural-Feedback-Loop Systems
May 06, 2025Abstract:Learning-enabled planning and control algorithms are increasingly popular, but they often lack rigorous guarantees of performance or safety. We introduce an algorithm for computing underapproximate backward reachable sets of nonlinear discrete time neural feedback loops. We then use the backward reachable sets to check goal-reaching properties. Our algorithm is based on overapproximating the system dynamics function to enable computation of underapproximate backward reachable sets through solutions of mixed-integer linear programs. We rigorously analyze the soundness of our algorithm and demonstrate it on a numerical example. Our work expands the class of properties that can be verified for learning-enabled systems.
TTT: A Temporal Refinement Heuristic for Tenuously Tractable Discrete Time Reachability Problems
Jul 19, 2024Abstract:Reachable set computation is an important tool for analyzing control systems. Simulating a control system can show that the system is generally functioning as desired, but a formal tool like reachability analysis can provide a guarantee of correctness. For linear systems, reachability analysis is straightforward and fast, but as more complex components are added to the control system such as nonlinear dynamics or a neural network controller, reachability analysis may slow down or become overly conservative. To address these challenges, much literature has focused on spatial refinement, e.g., tuning the discretization of the input sets and intermediate reachable sets. However, this paper addresses a different dimension: temporal refinement. The basic idea of temporal refinement is to automatically choose when along the horizon of the reachability problem to execute slow symbolic queries which incur less approximation error versus fast concrete queries which incur more approximation error. Temporal refinement can be combined with other refinement approaches and offers an additional ``tuning knob'' with which to trade off tractability and tightness in approximate reachable set computation. Here, we introduce an automatic framework for performing temporal refinement and we demonstrate the effectiveness of this technique on computing approximate reachable sets for nonlinear systems with neural network control policies. We demonstrate the calculation of reachable sets of varying approximation error under varying computational budget and show that our algorithm is able to generate approximate reachable sets with a similar amount of error to the baseline approach in 20-70% less time.
Backward Reachability Analysis of Neural Feedback Loops: Techniques for Linear and Nonlinear Systems
Sep 28, 2022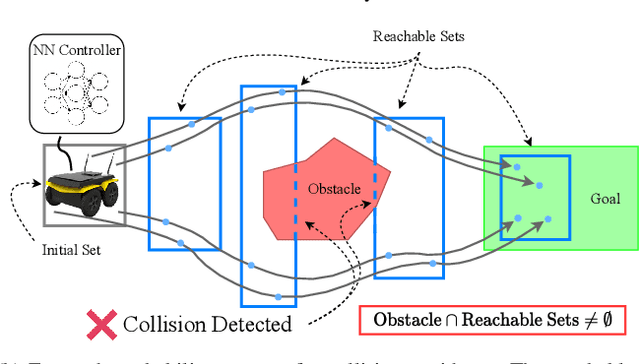


Abstract:The increasing prevalence of neural networks (NNs) in safety-critical applications calls for methods to certify safe behavior. This paper presents a backward reachability approach for safety verification of neural feedback loops (NFLs), i.e., closed-loop systems with NN control policies. While recent works have focused on forward reachability as a strategy for safety certification of NFLs, backward reachability offers advantages over the forward strategy, particularly in obstacle avoidance scenarios. Prior works have developed techniques for backward reachability analysis for systems without NNs, but the presence of NNs in the feedback loop presents a unique set of problems due to the nonlinearities in their activation functions and because NN models are generally not invertible. To overcome these challenges, we use existing forward NN analysis tools to efficiently find an over-approximation of the backprojection (BP) set, i.e., the set of states for which the NN control policy will drive the system to a given target set. We present frameworks for calculating BP over-approximations for both linear and nonlinear systems with control policies represented by feedforward NNs and propose computationally efficient strategies. We use numerical results from a variety of models to showcase the proposed algorithms, including a demonstration of safety certification for a 6D system.
Verifying Inverse Model Neural Networks
Feb 04, 2022


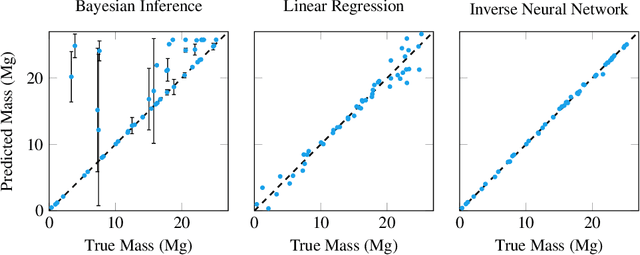
Abstract:Inverse problems exist in a wide variety of physical domains from aerospace engineering to medical imaging. The goal is to infer the underlying state from a set of observations. When the forward model that produced the observations is nonlinear and stochastic, solving the inverse problem is very challenging. Neural networks are an appealing solution for solving inverse problems as they can be trained from noisy data and once trained are computationally efficient to run. However, inverse model neural networks do not have guarantees of correctness built-in, which makes them unreliable for use in safety and accuracy-critical contexts. In this work we introduce a method for verifying the correctness of inverse model neural networks. Our approach is to overapproximate a nonlinear, stochastic forward model with piecewise linear constraints and encode both the overapproximate forward model and the neural network inverse model as a mixed-integer program. We demonstrate this verification procedure on a real-world airplane fuel gauge case study. The ability to verify and consequently trust inverse model neural networks allows their use in a wide variety of contexts, from aerospace to medicine.
OVERT: An Algorithm for Safety Verification of Neural Network Control Policies for Nonlinear Systems
Aug 03, 2021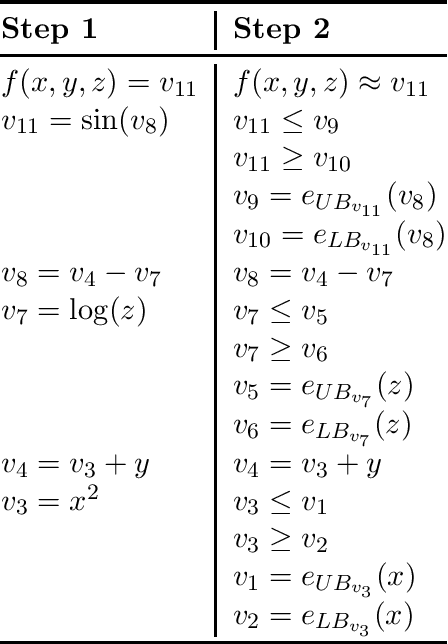



Abstract:Deep learning methods can be used to produce control policies, but certifying their safety is challenging. The resulting networks are nonlinear and often very large. In response to this challenge, we present OVERT: a sound algorithm for safety verification of nonlinear discrete-time closed loop dynamical systems with neural network control policies. The novelty of OVERT lies in combining ideas from the classical formal methods literature with ideas from the newer neural network verification literature. The central concept of OVERT is to abstract nonlinear functions with a set of optimally tight piecewise linear bounds. Such piecewise linear bounds are designed for seamless integration into ReLU neural network verification tools. OVERT can be used to prove bounded-time safety properties by either computing reachable sets or solving feasibility queries directly. We demonstrate various examples of safety verification for several classical benchmark examples. OVERT compares favorably to existing methods both in computation time and in tightness of the reachable set.
Machine Learning for Generalizable Prediction of Flood Susceptibility
Oct 15, 2019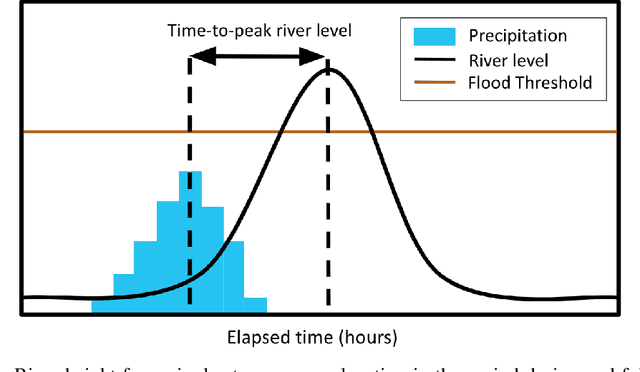

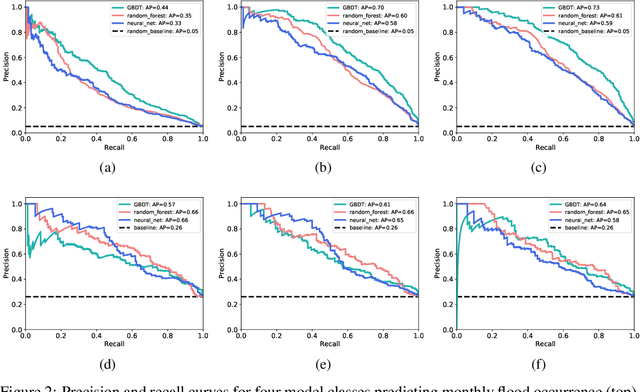
Abstract:Flooding is a destructive and dangerous hazard and climate change appears to be increasing the frequency of catastrophic flooding events around the world. Physics-based flood models are costly to calibrate and are rarely generalizable across different river basins, as model outputs are sensitive to site-specific parameters and human-regulated infrastructure. In contrast, statistical models implicitly account for such factors through the data on which they are trained. Such models trained primarily from remotely-sensed Earth observation data could reduce the need for extensive in-situ measurements. In this work, we develop generalizable, multi-basin models of river flooding susceptibility using geographically-distributed data from the USGS stream gauge network. Machine learning models are trained in a supervised framework to predict two measures of flood susceptibility from a mix of river basin attributes, impervious surface cover information derived from satellite imagery, and historical records of rainfall and stream height. We report prediction performance of multiple models using precision-recall curves, and compare with performance of naive baselines. This work on multi-basin flood prediction represents a step in the direction of making flood prediction accessible to all at-risk communities.
HG-DAgger: Interactive Imitation Learning with Human Experts
Mar 11, 2019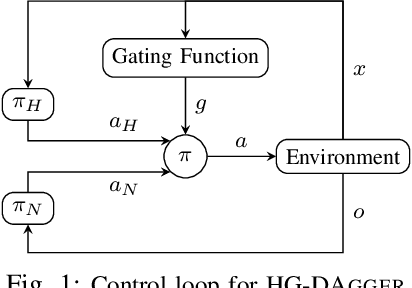

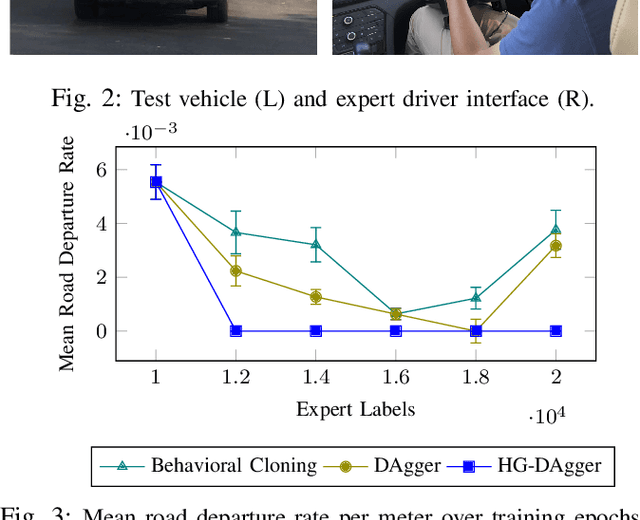
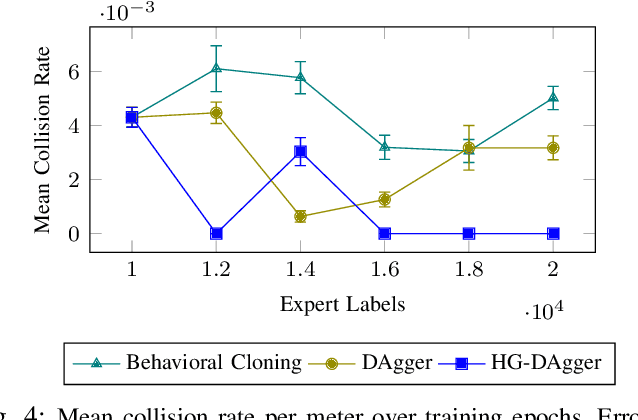
Abstract:Imitation learning has proven to be useful for many real-world problems, but approaches such as behavioral cloning suffer from data mismatch and compounding error issues. One attempt to address these limitations is the DAgger algorithm, which uses the state distribution induced by the novice to sample corrective actions from the expert. Such sampling schemes, however, require the expert to provide action labels without being fully in control of the system. This can decrease safety and, when using humans as experts, is likely to degrade the quality of the collected labels due to perceived actuator lag. In this work, we propose HG-DAgger, a variant of DAgger that is more suitable for interactive imitation learning from human experts in real-world systems. In addition to training a novice policy, HG-DAgger also learns a safety threshold for a model-uncertainty-based risk metric that can be used to predict the performance of the fully trained novice in different regions of the state space. We evaluate our method on both a simulated and real-world autonomous driving task, and demonstrate improved performance over both DAgger and behavioral cloning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge