DYNUS: Uncertainty-aware Trajectory Planner in Dynamic Unknown Environments

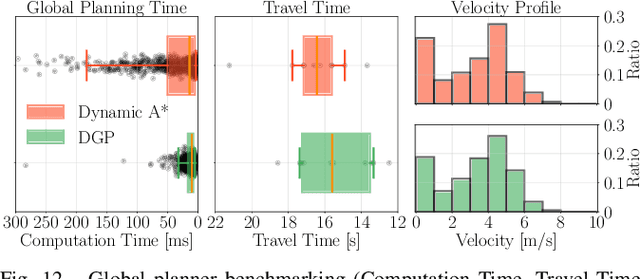
This paper introduces DYNUS, an uncertainty-aware trajectory planner designed for dynamic unknown environments. Operating in such settings presents many challenges -- most notably, because the agent cannot predict the ground-truth future paths of obstacles, a previously planned trajectory can become unsafe at any moment, requiring rapid replanning to avoid collisions. Recently developed planners have used soft-constraint approaches to achieve the necessary fast computation times; however, these methods do not guarantee collision-free paths even with static obstacles. In contrast, hard-constraint methods ensure collision-free safety, but typically have longer computation times. To address these issues, we propose three key contributions. First, the DYNUS Global Planner (DGP) and Temporal Safe Corridor Generation operate in spatio-temporal space and handle both static and dynamic obstacles in the 3D environment. Second, the Safe Planning Framework leverages a combination of exploratory, safe, and contingency trajectories to flexibly re-route when potential future collisions with dynamic obstacles are detected. Finally, the Fast Hard-Constraint Local Trajectory Formulation uses a variable elimination approach to reduce the problem size and enable faster computation by pre-computing dependencies between free and dependent variables while still ensuring collision-free trajectories. We evaluated DYNUS in a variety of simulations, including dense forests, confined office spaces, cave systems, and dynamic environments. Our experiments show that DYNUS achieves a success rate of 100% and travel times that are approximately 25.0% faster than state-of-the-art methods. We also evaluated DYNUS on multiple platforms -- a quadrotor, a wheeled robot, and a quadruped -- in both simulation and hardware experiments.

Safe Autonomy for Uncrewed Surface Vehicles Using Adaptive Control and Reachability Analysis

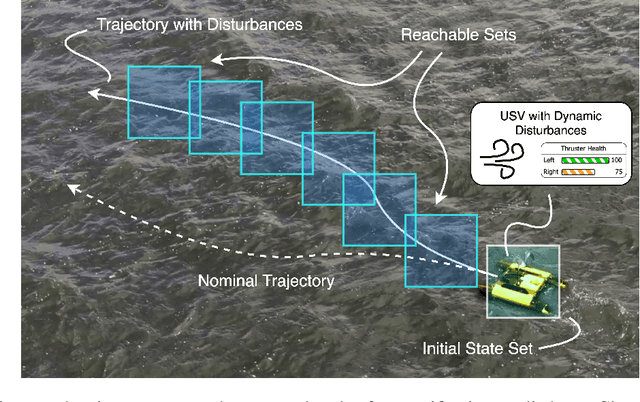
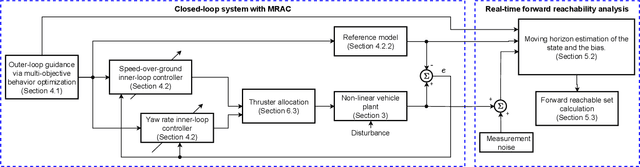
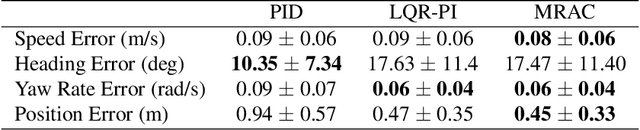
Marine robots must maintain precise control and ensure safety during tasks like ocean monitoring, even when encountering unpredictable disturbances that affect performance. Designing algorithms for uncrewed surface vehicles (USVs) requires accounting for these disturbances to control the vehicle and ensure it avoids obstacles. While adaptive control has addressed USV control challenges, real-world applications are limited, and certifying USV safety amidst unexpected disturbances remains difficult. To tackle control issues, we employ a model reference adaptive controller (MRAC) to stabilize the USV along a desired trajectory. For safety certification, we developed a reachability module with a moving horizon estimator (MHE) to estimate disturbances affecting the USV. This estimate is propagated through a forward reachable set calculation, predicting future states and enabling real-time safety certification. We tested our safe autonomy pipeline on a Clearpath Heron USV in the Charles River, near MIT. Our experiments demonstrated that the USV's MRAC controller and reachability module could adapt to disturbances like thruster failures and drag forces. The MRAC controller outperformed a PID baseline, showing a 45%-81% reduction in RMSE position error. Additionally, the reachability module provided real-time safety certification, ensuring the USV's safety. We further validated our pipeline's effectiveness in underway replenishment and canal scenarios, simulating relevant marine tasks.

Reduced Order Model of a Generic Submarine for Maneuvering Near the Surface

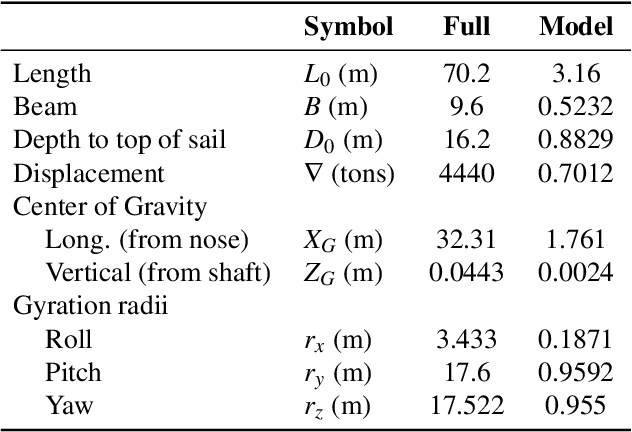
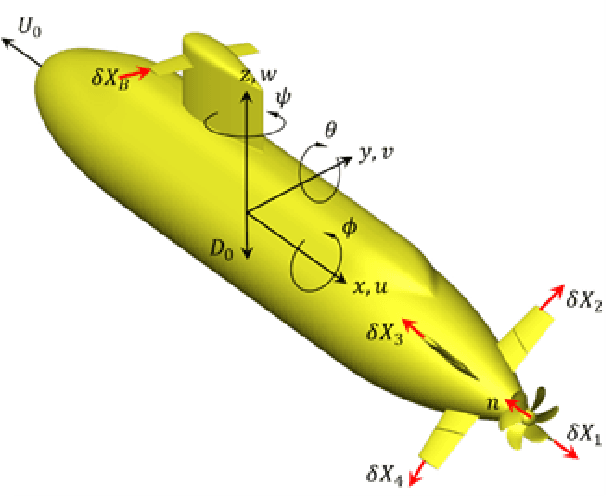
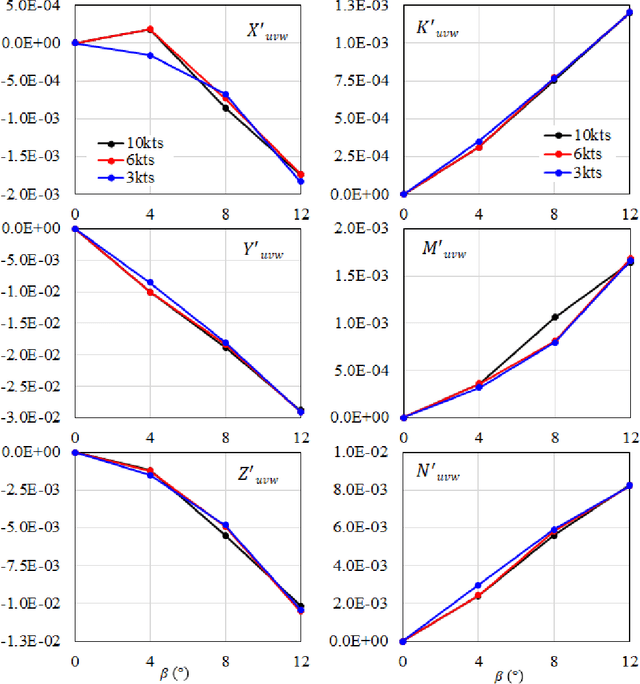
A reduced order model of a generic submarine is presented. Computational fluid dynamics (CFD) results are used to create and validate a model that includes depth dependence and the effect of waves on the craft. The model and the procedure to obtain its coefficients are discussed, and examples of the data used to obtain the model coefficients are presented. An example of operation following a complex path is presented and results from the reduced order model are compared to those from an equivalent CFD calculation. The controller implemented to complete these maneuvers is also presented.

A Hybrid Partitioning Strategy for Backward Reachability of Neural Feedback Loops

As neural networks become more integrated into the systems that we depend on for transportation, medicine, and security, it becomes increasingly important that we develop methods to analyze their behavior to ensure that they are safe to use within these contexts. The methods used in this paper seek to certify safety for closed-loop systems with neural network controllers, i.e., neural feedback loops, using backward reachability analysis. Namely, we calculate backprojection (BP) set over-approximations (BPOAs), i.e., sets of states that lead to a given target set that bounds dangerous regions of the state space. The system's safety can then be certified by checking its current state against the BPOAs. While over-approximating BPs is significantly faster than calculating exact BP sets, solving the relaxed problem leads to conservativeness. To combat conservativeness, partitioning strategies can be used to split the problem into a set of sub-problems, each less conservative than the unpartitioned problem. We introduce a hybrid partitioning method that uses both target set partitioning (TSP) and backreachable set partitioning (BRSP) to overcome a lower bound on estimation error that is present when using BRSP. Numerical results demonstrate a near order-of-magnitude reduction in estimation error compared to BRSP or TSP given the same computation time.

Backward Reachability Analysis of Neural Feedback Loops: Techniques for Linear and Nonlinear Systems

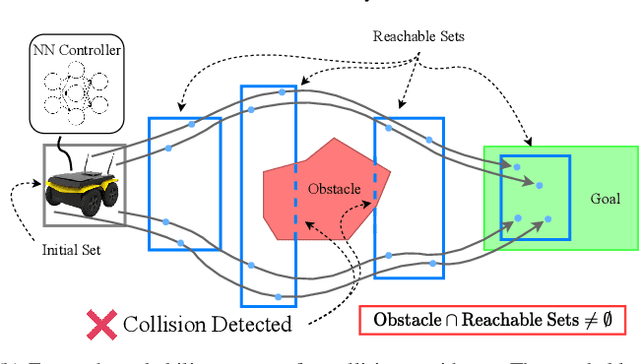
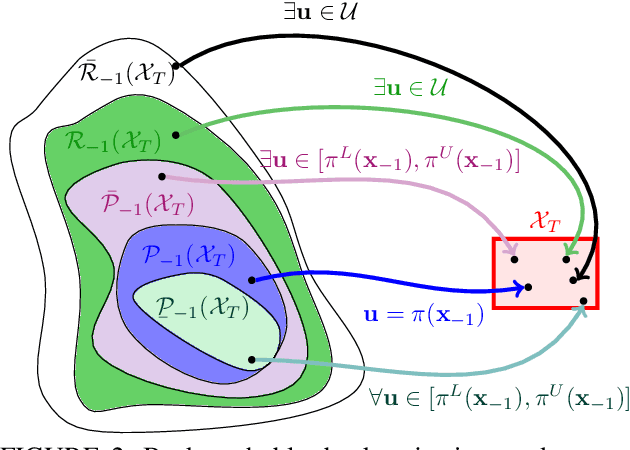
The increasing prevalence of neural networks (NNs) in safety-critical applications calls for methods to certify safe behavior. This paper presents a backward reachability approach for safety verification of neural feedback loops (NFLs), i.e., closed-loop systems with NN control policies. While recent works have focused on forward reachability as a strategy for safety certification of NFLs, backward reachability offers advantages over the forward strategy, particularly in obstacle avoidance scenarios. Prior works have developed techniques for backward reachability analysis for systems without NNs, but the presence of NNs in the feedback loop presents a unique set of problems due to the nonlinearities in their activation functions and because NN models are generally not invertible. To overcome these challenges, we use existing forward NN analysis tools to efficiently find an over-approximation of the backprojection (BP) set, i.e., the set of states for which the NN control policy will drive the system to a given target set. We present frameworks for calculating BP over-approximations for both linear and nonlinear systems with control policies represented by feedforward NNs and propose computationally efficient strategies. We use numerical results from a variety of models to showcase the proposed algorithms, including a demonstration of safety certification for a 6D system.

Backward Reachability Analysis for Neural Feedback Loops

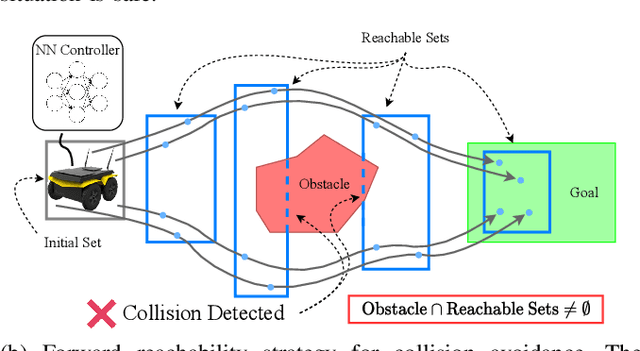
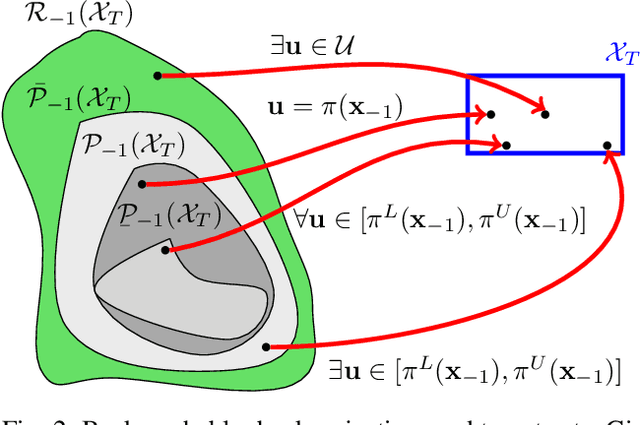
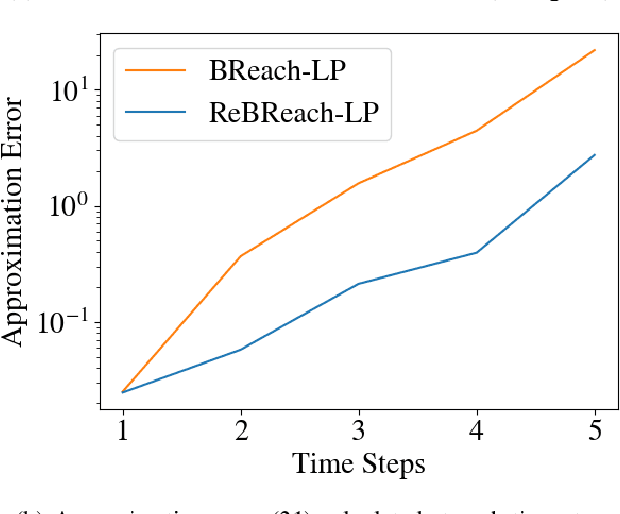
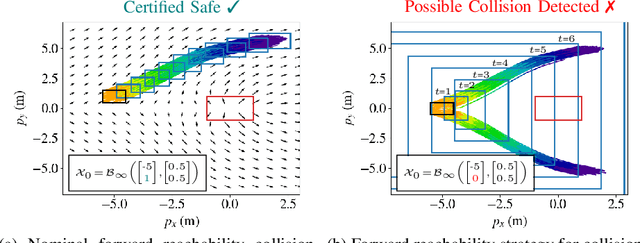
The increasing prevalence of neural networks (NNs) in safety-critical applications calls for methods to certify their behavior and guarantee safety. This paper presents a backward reachability approach for safety verification of neural feedback loops (NFLs), i.e., closed-loop systems with NN control policies. While recent works have focused on forward reachability as a strategy for safety certification of NFLs, backward reachability offers advantages over the forward strategy, particularly in obstacle avoidance scenarios. Prior works have developed techniques for backward reachability analysis for systems without NNs, but the presence of NNs in the feedback loop presents a unique set of problems due to the nonlinearities in their activation functions and because NN models are generally not invertible. To overcome these challenges, we use existing forward NN analysis tools to find affine bounds on the control inputs and solve a series of linear programs (LPs) to efficiently find an approximation of the backprojection (BP) set, i.e., the set of states for which the NN control policy will drive the system to a given target set. We present an algorithm to iteratively find BP set estimates over a given time horizon and demonstrate the ability to reduce conservativeness in the BP set estimates by up to 88% with low additional computational cost. We use numerical results from a double integrator model to verify the efficacy of these algorithms and demonstrate the ability to certify safety for a linearized ground robot model in a collision avoidance scenario where forward reachability fails.