Quasi-Static Continuum Model of Octopus-Like Soft Robot Arm Under Water Actuated by Twisted and Coiled Artificial Muscles (TCAMs)

The current work is a qualitative study that aims to explore the implementation of Twisted and Coiled Artificial Muscles (TCAMs) for actuating and replicating the bending motion of an octopus-like soft robot arm underwater. Additionally, it investigates the impact of hydrostatic and dynamic forces from steady-state fluid flow on the arm's motion. The artificial muscles are lightweight and low-cost actuators that generate a high power-to-weight ratio, producing tensile force up to 12,600 times their own weight, which is close to the functionality of biological muscles. The "extended" Cosserat theory of rods is employed to formulate a quasi-static continuum model of arm motion, where the arm's cross-section is not only capable of rigid rotation but also deforms within its plane. This planar deformation of the arm cross-section aligns with the biological behavior of the octopus arm, where the stiffness of the hydrostat is directly induced by the incompressibility of the tissues. In line with the main goal, a constitutive model is derived for the material of the octopus arm to capture its characteristic behavior.

Path Planning for Continuum Rods Using Bernstein Surfaces

This paper presents a method for optimal motion planning of continuum robots by employing Bernstein surfaces to approximate the system's dynamics and impose complex constraints, including collision avoidance. The main contribution is the approximation of infinite-dimensional continuous problems into their discrete counterparts, facilitating their solution using standard optimization solvers. This discretization leverages the unique properties of Bernstein surface, providing a framework that extends previous works which focused on ODEs approximated by Bernstein polynomials. Numerical validations are conducted through several numerical scenarios. The presented methodology offers a promising direction for solving complex optimal control problems in the realm of soft robotics.

Bioinspired Soft Robotics: state of the art, challenges, and future directions

Purpose of Review: This review provides an overview of the state of the art in bioinspired soft robotics with by examining advancements in actuation, functionality, modeling, and control. Recent Findings: Recent research into actuation methods, such as artificial muscles, have expanded the functionality and potential use of bioinspired soft robots. Additionally, the application of finite dimensional models has improved computational efficiency for modeling soft continuum systems, and garnered interest as a basis for controller formulation. Summary: Bioinspiration in the field of soft robotics has led to diverse approaches to problems in a range of task spaces. In particular, new capabilities in system simplification, miniaturization, and untethering have each contributed to the field's growth. There is still significant room for improvement in the streamlining of design and manufacturing for these systems, as well as in their control.

Reduced Order Model of a Generic Submarine for Maneuvering Near the Surface

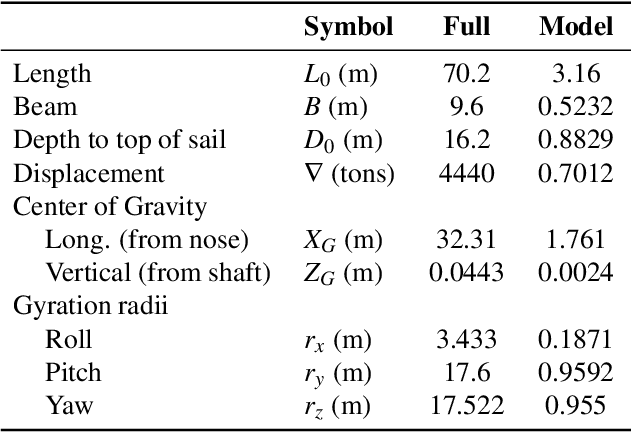
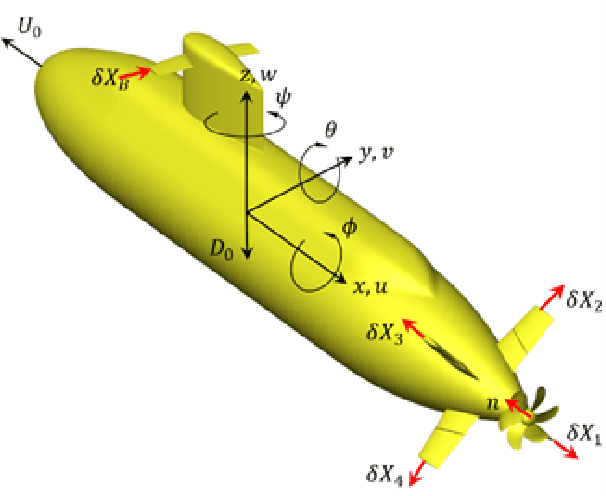
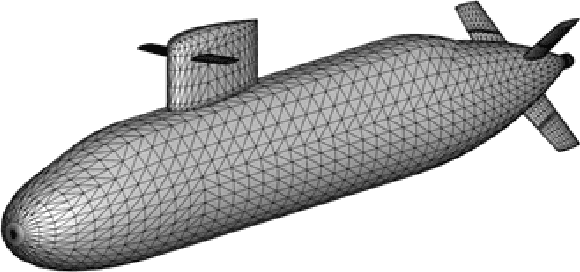
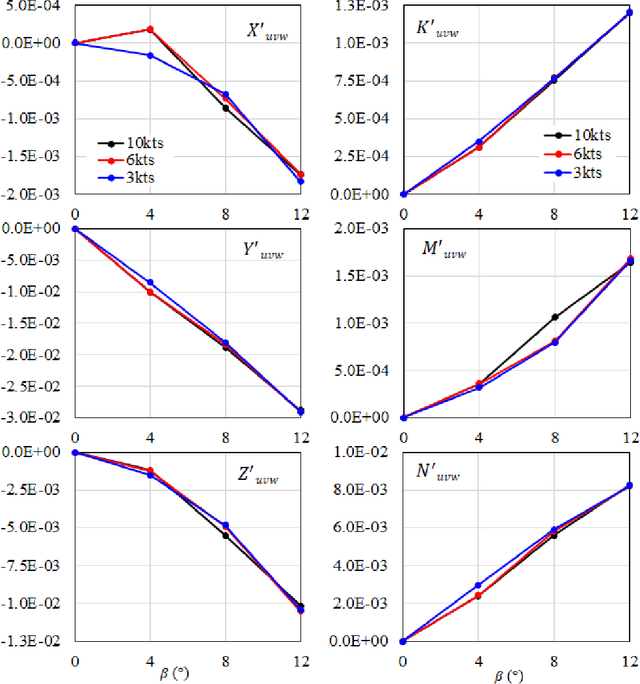
A reduced order model of a generic submarine is presented. Computational fluid dynamics (CFD) results are used to create and validate a model that includes depth dependence and the effect of waves on the craft. The model and the procedure to obtain its coefficients are discussed, and examples of the data used to obtain the model coefficients are presented. An example of operation following a complex path is presented and results from the reduced order model are compared to those from an equivalent CFD calculation. The controller implemented to complete these maneuvers is also presented.

Active Localization using Bernstein Distribution Functions

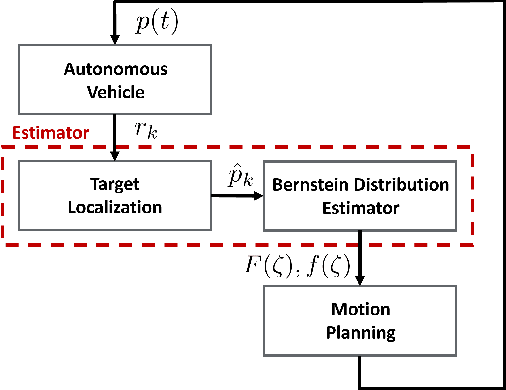
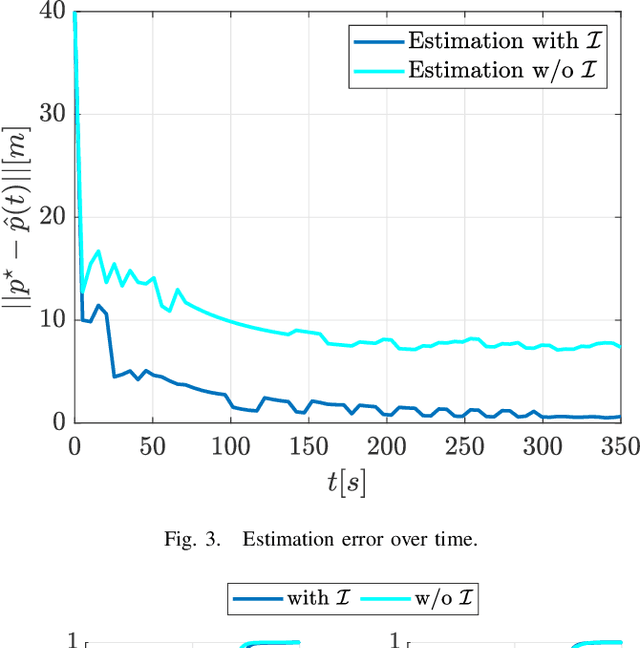
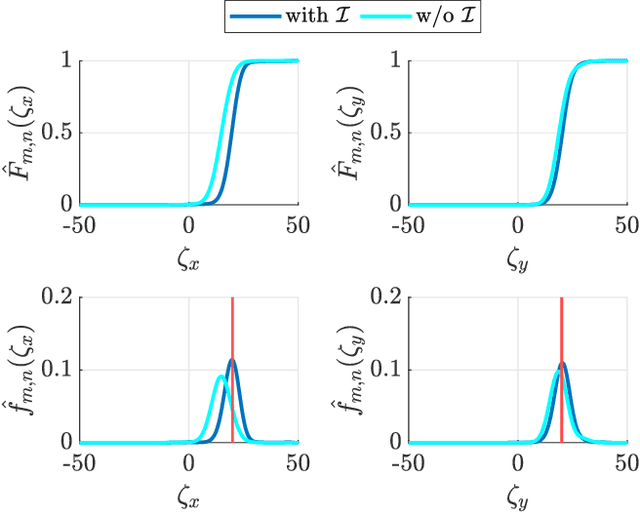
In this work, we present a framework that enables a vehicle to autonomously localize a target based on noisy range measurements computed from RSSI data. To achieve the mission objectives, we develop a control scheme composed of two main parts: an estimator and a motion planner. At each time step, new estimates of the target's position are computed and used to generate and update distribution functions using Bernstein polynomials. A metric of the efficiency of the estimator is derived based on the Fisher Information Matrix. Finally, the motion planning problem is formulated to react in real time to new information about the target and improve the estimator's performance.

Biologically Inspired Collision Avoidance Without Distance Information

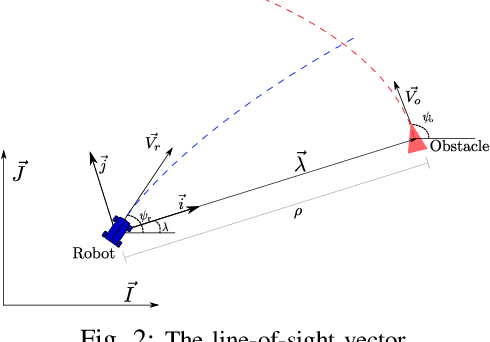
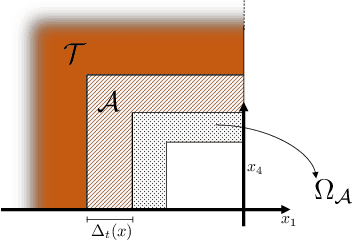
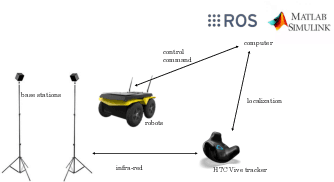
Biological evidence shows that animals are capable of evading eminent collision without using depth information, relying solely on looming stimuli. In robotics, collision avoidance among uncooperative vehicles requires measurement of relative distance to the obstacle. Small, low-cost mobile robots and UAVs might be unable to carry distance measuring sensors, like LIDARS and depth cameras. We propose a control framework suitable for a unicycle-like vehicle moving in a 2D plane that achieves collision avoidance. The control strategy is inspired by the reaction of invertebrates to approaching obstacles, relying exclusively on line-of-sight (LOS) angle, LOS angle rate, and time-to-collision as feedback. Those quantities can readily be estimated from a monocular camera vision system onboard a mobile robot. The proposed avoidance law commands the heading angle to circumvent a moving obstacle with unknown position, while the velocity controller is left as a degree of freedom to accomplish other mission objectives. Theoretical guarantees are provided to show that minimum separation between the vehicle and the obstacle is attained regardless of the exogenous tracking controller.

Bernstein polynomial-based transcription method for solving optimal trajectory generation problems

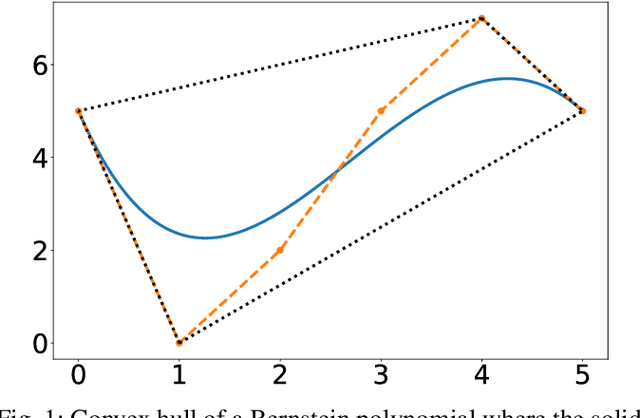
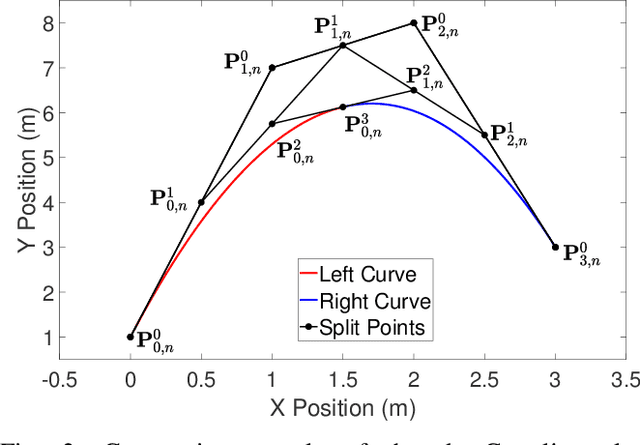
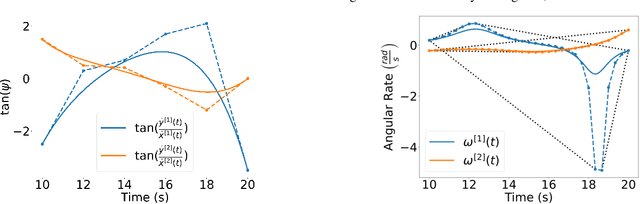
This paper presents a method and an open-source implementation, Bernstein/B\'ezier Optimal Trajectories (BeBOT), for the generation of trajectories for autonomous system operations. The proposed method is based on infinite dimensional optimal control formulations of trajectory generation problems. By approximating the trajectories using Bernstein polynomials, these problems can be transcribed as nonlinear programming problems, which can then be solved using off-the-shelf solvers. Bernstein polynomials possess favorable geometric properties that enable the trajectory planner to efficiently evaluate and enforce constraints along the vehicles' trajectories, including maximum speed and angular rates, minimum distance between trajectories and between the vehicles and obstacles. By virtue of these properties, feasibility and safety constraints typically imposed in autonomous vehicle operations can be enforced and guaranteed independently on the order of the polynomials. Thus, the trajectory generation algorithm can efficiently generate feasible and collision-free trajectories, and can be deployed for real-time safety critical applications in complex environments and for multiple vehicle missions.

Proximity Queries for Absolutely Continuous Parametric Curves

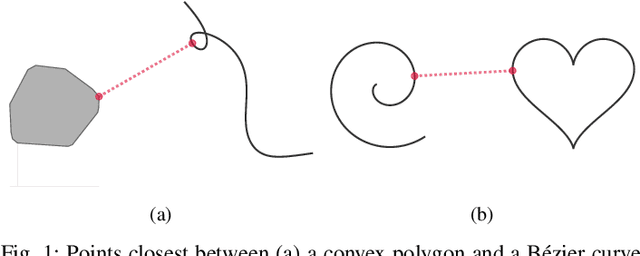
In motion planning problems for autonomous robots, such as self-driving cars, the robot must ensure that its planned path is not in close proximity to obstacles in the environment. However, the problem of evaluating the proximity is generally non-convex and serves as a significant computational bottleneck for motion planning algorithms. In this paper, we present methods for a general class of absolutely continuous parametric curves to compute: (i) the minimum separating distance, (ii) tolerance verification, and (iii) collision detection. Our methods efficiently compute bounds on obstacle proximity by bounding the curve in a convex region. This bound is based on an upper bound on the curve arc length that can be expressed in closed form for a useful class of parametric curves including curves with trigonometric or polynomial bases. We demonstrate the computational efficiency and accuracy of our approach through numerical simulations of several proximity problems.

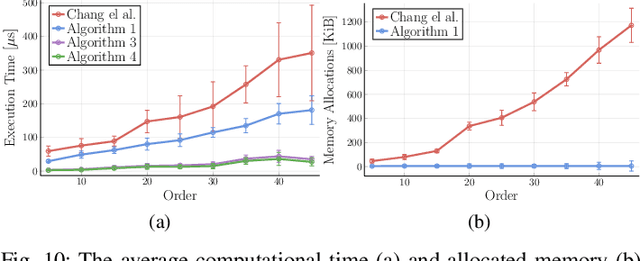
Bernstein approximation of optimal control problems

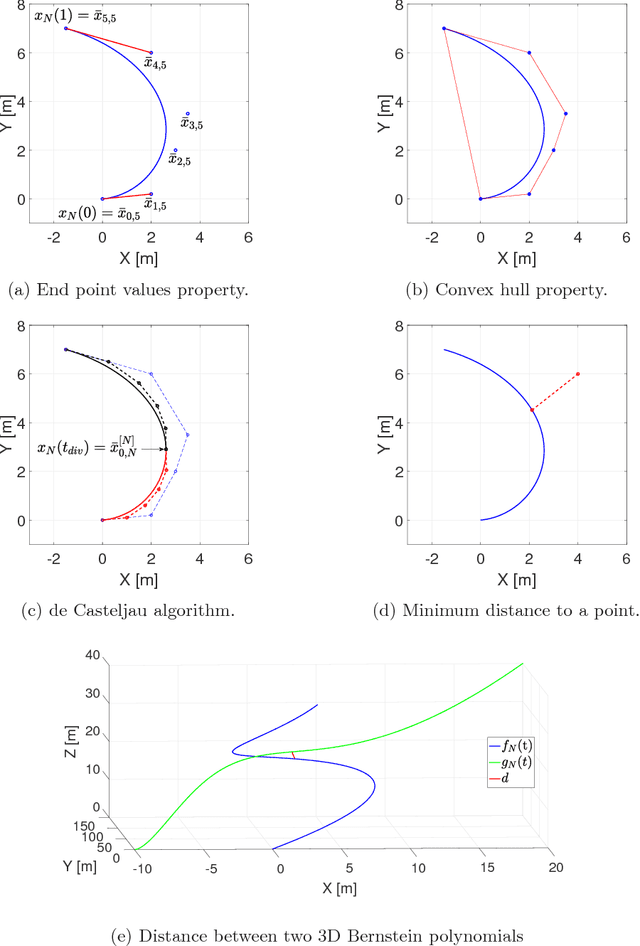
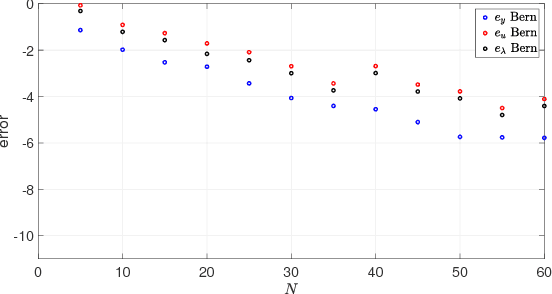
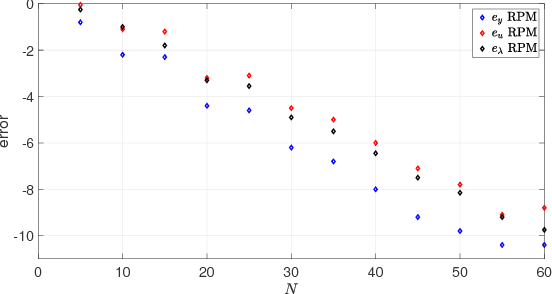
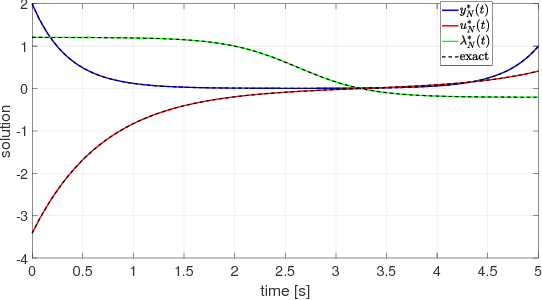
Bernstein polynomial approximation to a continuous function has a slower rate of convergence as compared to other approximation methods. "The fact seems to have precluded any numerical application of Bernstein polynomials from having been made. Perhaps they will find application when the properties of the approximant in the large are of more importance than the closeness of the approximation." -- has remarked P.J. Davis in his 1963 book Interpolation and Approximation. This paper presents a direct approximation method for nonlinear optimal control problems with mixed input and state constraints based on Bernstein polynomial approximation. We provide a rigorous analysis showing that the proposed method yields consistent approximations of time continuous optimal control problems. Furthermore, we demonstrate that the proposed method can also be used for costate estimation of the optimal control problems. This latter result leads to the formulation of the Covector Mapping Theorem for Bernstein polynomial approximation. Finally, we explore the numerical and geometric properties of Bernstein polynomials, and illustrate the advantages of the proposed approximation method through several numerical examples.