$\mathcal{L}_1$Quad: $\mathcal{L}_1$ Adaptive Augmentation of Geometric Control for Agile Quadrotors with Performance Guarantees

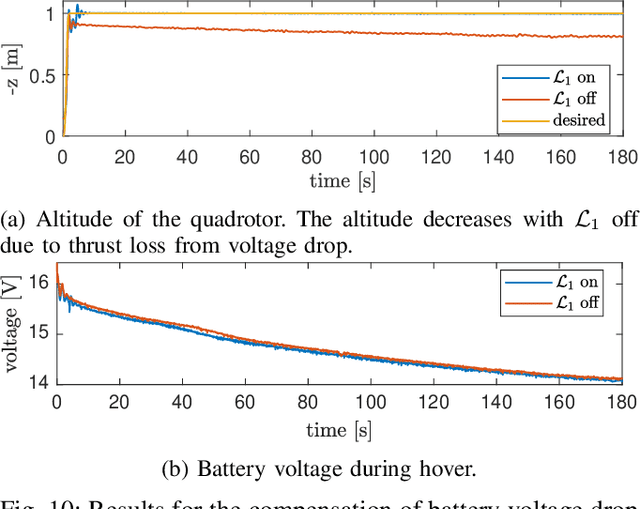
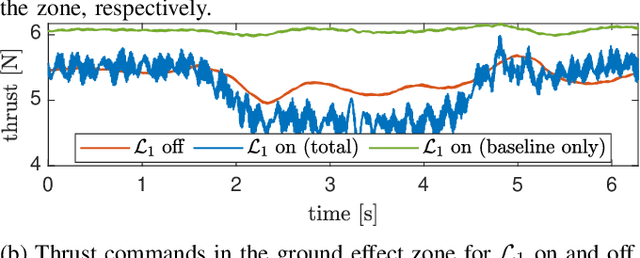
Quadrotors that can operate safely in the presence of imperfect model knowledge and external disturbances are crucial in safety-critical applications. We present L1Quad, a control architecture for quadrotors based on the L1 adaptive control. L1Quad enables safe tubes centered around a desired trajectory that the quadrotor is always guaranteed to remain inside. Our design applies to both the rotational and the translational dynamics of the quadrotor. We lump various types of uncertainties and disturbances as unknown nonlinear (time- and state-dependent) forces and moments. Without assuming or enforcing parametric structures, L1Quad can accurately estimate and compensate for these unknown forces and moments. Extensive experimental results demonstrate that L1Quad is able to significantly outperform baseline controllers under a variety of uncertainties with consistently small tracking errors.

$\mathcal{RL}_1$-$\mathcal{GP}$: Safe Simultaneous Learning and Control

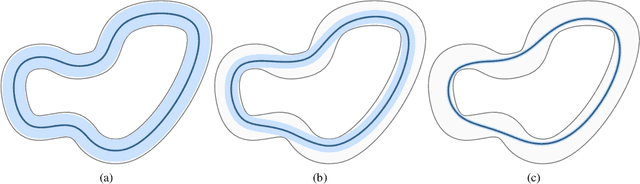
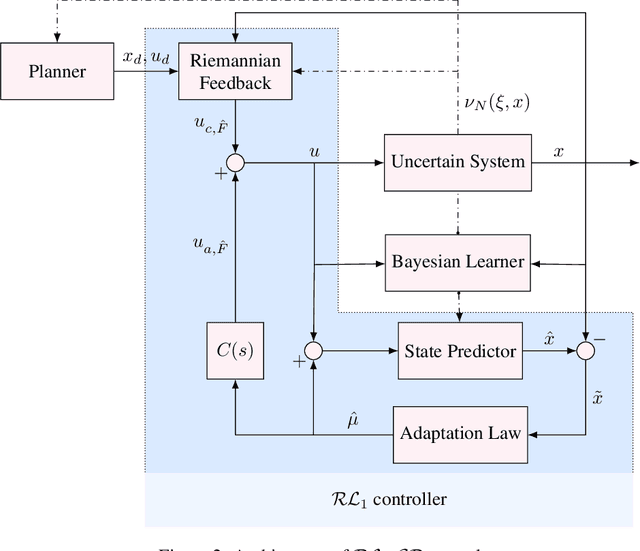
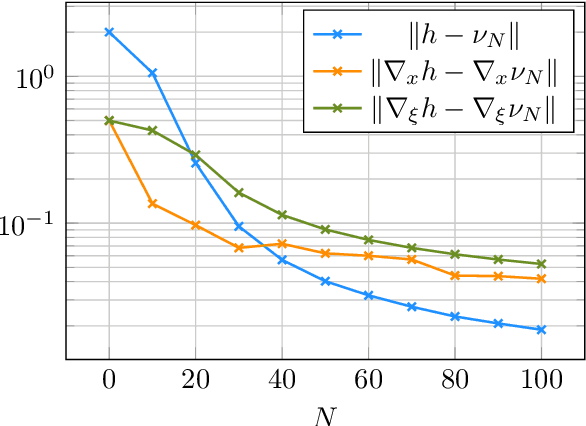
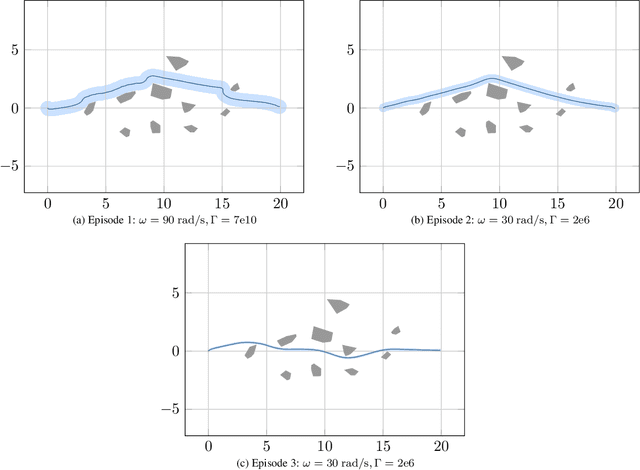
We present $\mathcal{RL}_1$-$\mathcal{GP}$, a control framework that enables safe simultaneous learning and control for systems subject to uncertainties. The two main constituents are Riemannian energy $\mathcal{L}_1$ ($\mathcal{RL}_1$) control and Bayesian learning in the form of Gaussian process (GP) regression. The $\mathcal{RL}_1$ controller ensures that control objectives are met while providing safety certificates. Furthermore, $\mathcal{RL}_1$-$\mathcal{GP}$ incorporates any available data into a GP model of uncertainties, which improves performance and enables the motion planner to achieve optimality safely. This way, the safe operation of the system is always guaranteed, even during the learning transients. We provide a few illustrative examples for the safe learning and control of planar quadrotor systems in a variety of environments.

Safe Feedback Motion Planning: A Contraction Theory and $\mathcal{L}_1$-Adaptive Control Based Approach

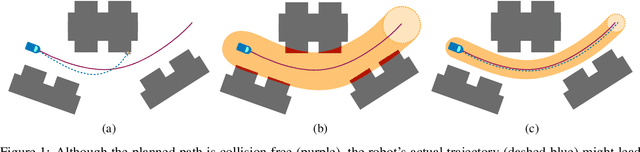
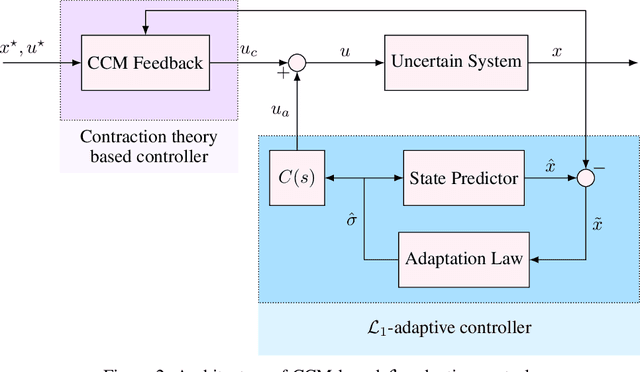
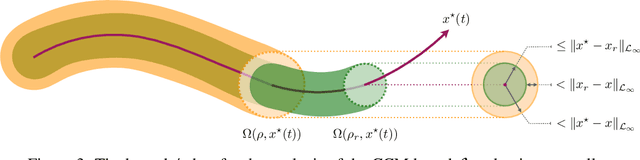
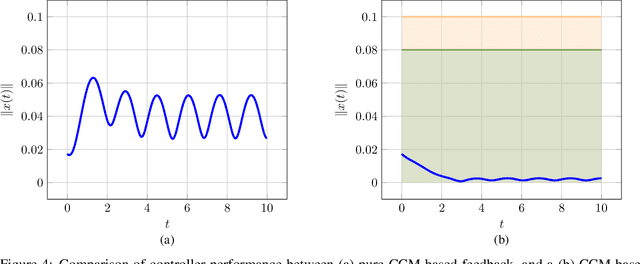
Autonomous robots that are capable of operating safely in the presence of imperfect model knowledge or external disturbances are vital in safety-critical applications. In this paper, we present a planner-agnostic framework to design and certify safe tubes around desired trajectories that the robot is always guaranteed to remain inside of. By leveraging recent results in contraction analysis and $\mathcal{L}_1$-adaptive control we synthesize an architecture that induces safe tubes for nonlinear systems with state and time-varying uncertainties. We demonstrate with a few illustrative examples how contraction theory-based $\mathcal{L}_1$-adaptive control can be used in conjunction with traditional motion planning algorithms to obtain provably safe trajectories.

Proximity Queries for Absolutely Continuous Parametric Curves

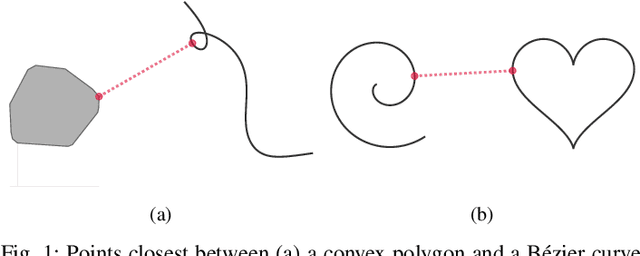
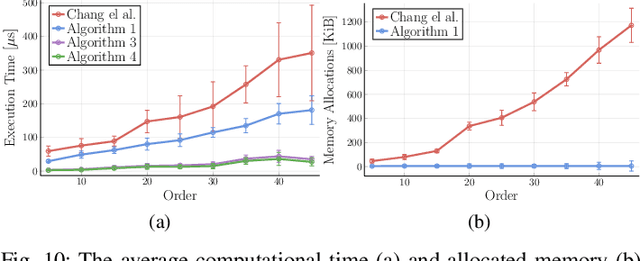
In motion planning problems for autonomous robots, such as self-driving cars, the robot must ensure that its planned path is not in close proximity to obstacles in the environment. However, the problem of evaluating the proximity is generally non-convex and serves as a significant computational bottleneck for motion planning algorithms. In this paper, we present methods for a general class of absolutely continuous parametric curves to compute: (i) the minimum separating distance, (ii) tolerance verification, and (iii) collision detection. Our methods efficiently compute bounds on obstacle proximity by bounding the curve in a convex region. This bound is based on an upper bound on the curve arc length that can be expressed in closed form for a useful class of parametric curves including curves with trigonometric or polynomial bases. We demonstrate the computational efficiency and accuracy of our approach through numerical simulations of several proximity problems.

Intent-Aware Probabilistic Trajectory Estimation for Collision Prediction with Uncertainty Quantification

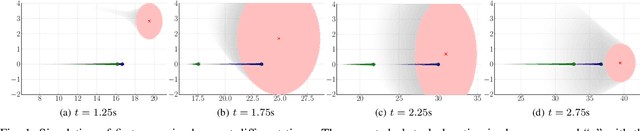
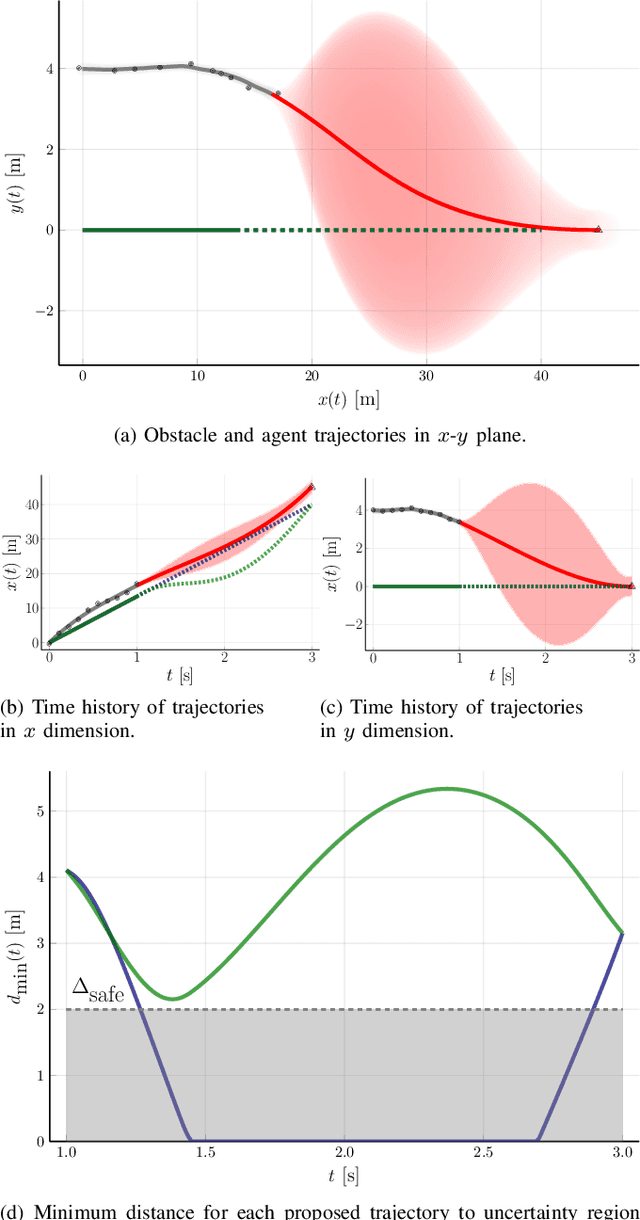
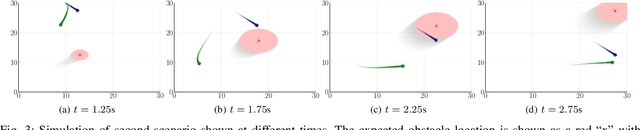
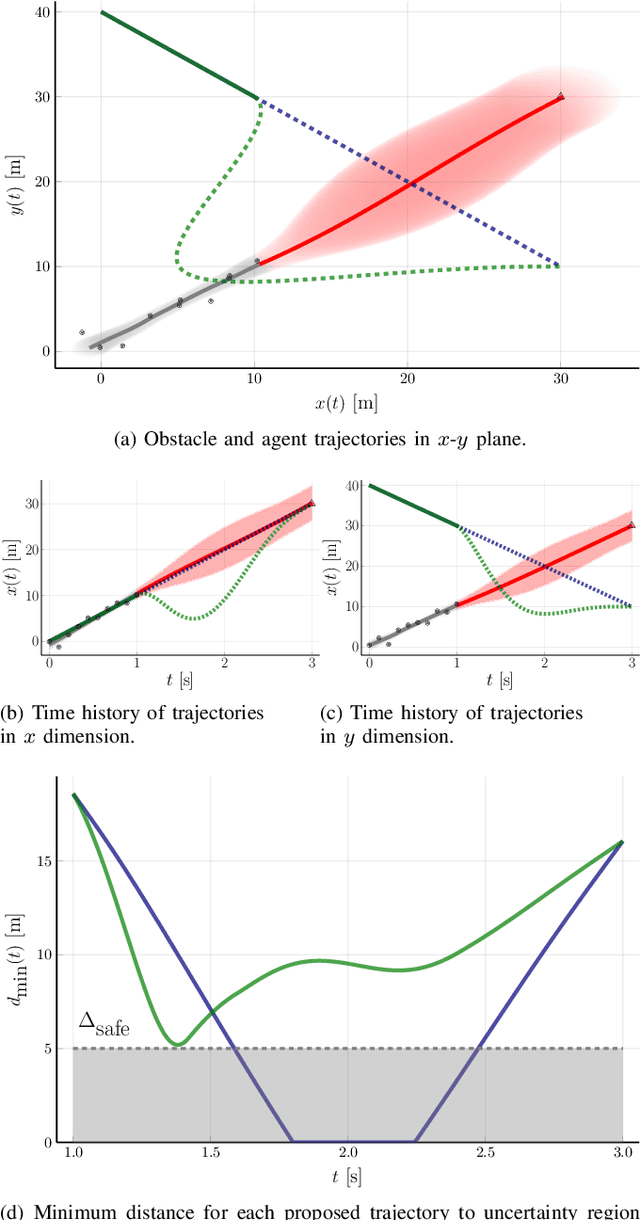
Collision prediction in a dynamic and unknown environment relies on knowledge of how the environment is changing. Many collision prediction methods rely on deterministic knowledge of how obstacles are moving in the environment. However, complete deterministic knowledge of the obstacles' motion is often unavailable. This work proposes a Gaussian process based prediction method that replaces the assumption of deterministic knowledge of each obstacle's future behavior with probabilistic knowledge, to allow a larger class of obstacles to be considered. The method solely relies on position and velocity measurements to predict collisions with dynamic obstacles. We show that the uncertainty region for obstacle positions can be expressed in terms of a combination of polynomials generated with Gaussian process regression. To control the growth of uncertainty over arbitrary time horizons, a probabilistic obstacle intention is assumed as a distribution over obstacle positions and velocities, which can be naturally included in the Gaussian process framework. Our approach is demonstrated in two case studies in which (i), an obstacle overtakes the agent and (ii), an obstacle crosses the agent's path perpendicularly. In these simulations we show that the collision can be predicted despite having limited knowledge of the obstacle's behavior.