Intent-Aware Probabilistic Trajectory Estimation for Collision Prediction with Uncertainty Quantification
Paper and Code
Apr 04, 2019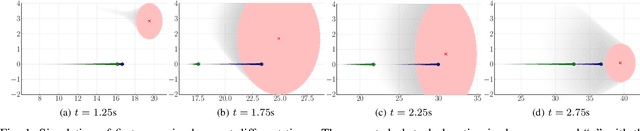
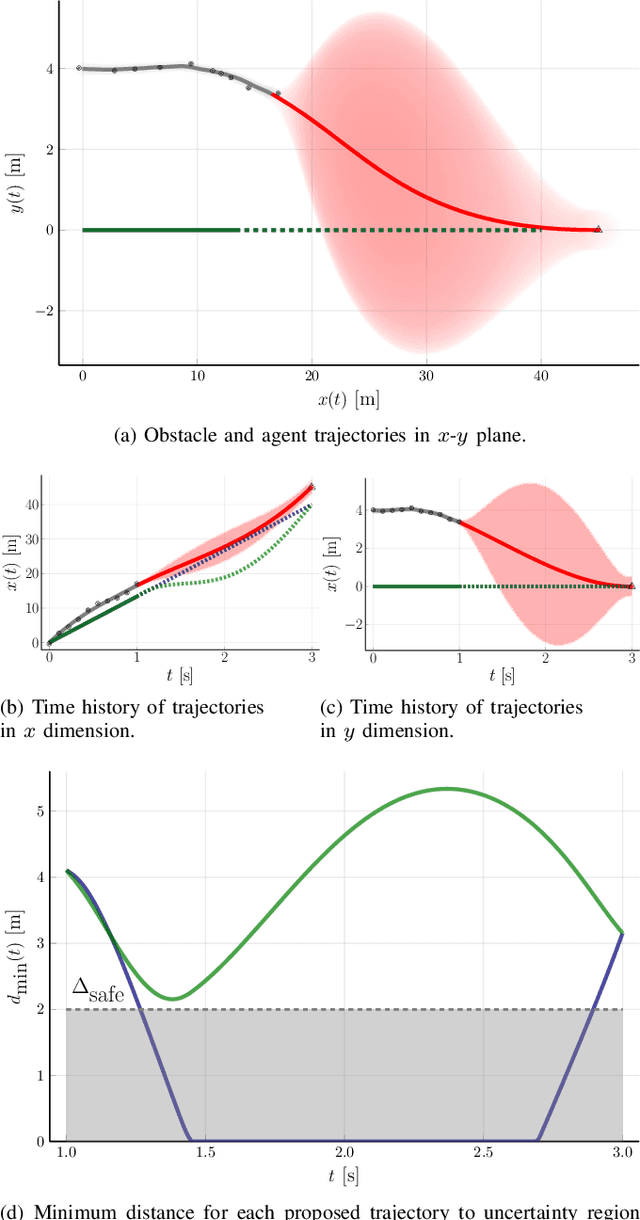
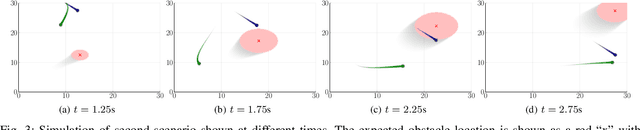
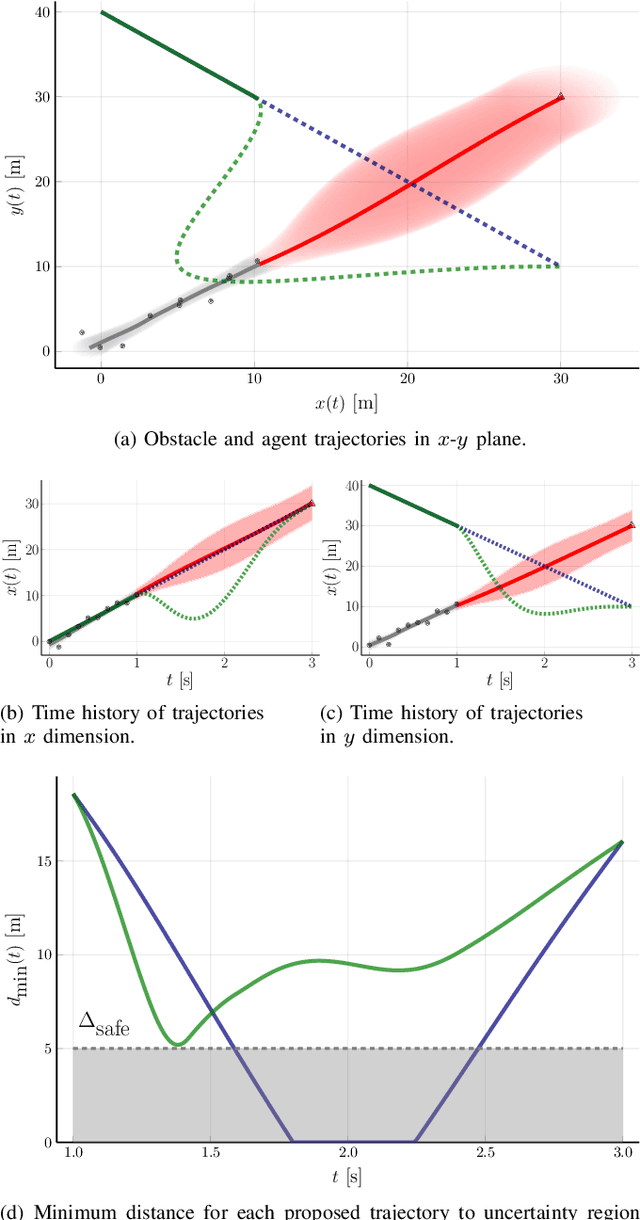
Collision prediction in a dynamic and unknown environment relies on knowledge of how the environment is changing. Many collision prediction methods rely on deterministic knowledge of how obstacles are moving in the environment. However, complete deterministic knowledge of the obstacles' motion is often unavailable. This work proposes a Gaussian process based prediction method that replaces the assumption of deterministic knowledge of each obstacle's future behavior with probabilistic knowledge, to allow a larger class of obstacles to be considered. The method solely relies on position and velocity measurements to predict collisions with dynamic obstacles. We show that the uncertainty region for obstacle positions can be expressed in terms of a combination of polynomials generated with Gaussian process regression. To control the growth of uncertainty over arbitrary time horizons, a probabilistic obstacle intention is assumed as a distribution over obstacle positions and velocities, which can be naturally included in the Gaussian process framework. Our approach is demonstrated in two case studies in which (i), an obstacle overtakes the agent and (ii), an obstacle crosses the agent's path perpendicularly. In these simulations we show that the collision can be predicted despite having limited knowledge of the obstacle's behavior.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge