Aditya Gahlawat
Robust Model Based Reinforcement Learning Using $\mathcal{L}_1$ Adaptive Control
Mar 21, 2024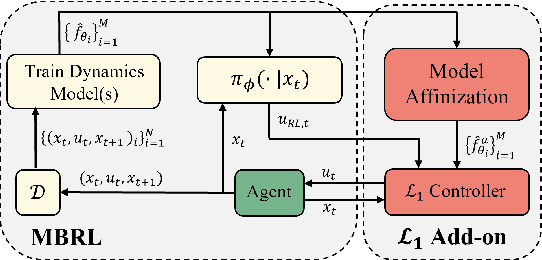
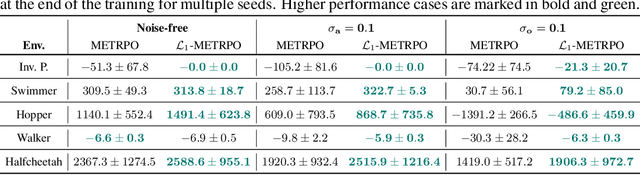
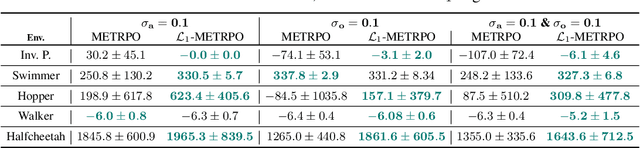
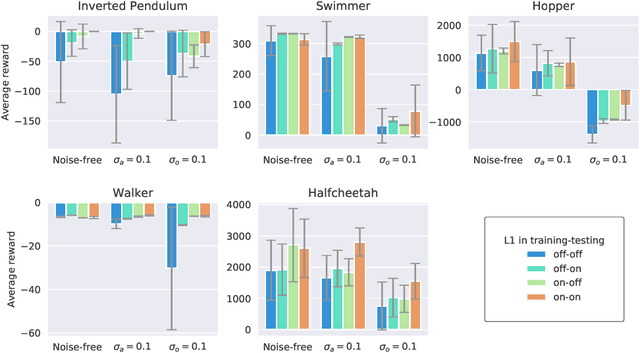
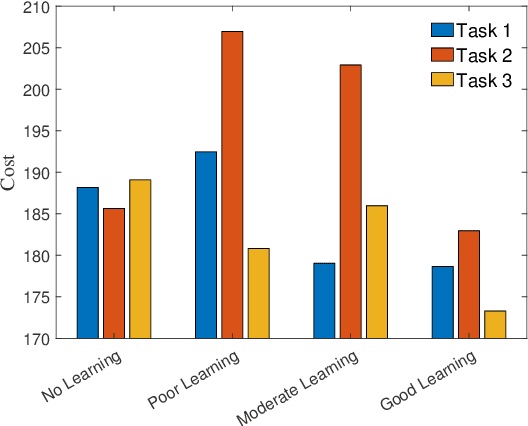
Abstract:We introduce $\mathcal{L}_1$-MBRL, a control-theoretic augmentation scheme for Model-Based Reinforcement Learning (MBRL) algorithms. Unlike model-free approaches, MBRL algorithms learn a model of the transition function using data and use it to design a control input. Our approach generates a series of approximate control-affine models of the learned transition function according to the proposed switching law. Using the approximate model, control input produced by the underlying MBRL is perturbed by the $\mathcal{L}_1$ adaptive control, which is designed to enhance the robustness of the system against uncertainties. Importantly, this approach is agnostic to the choice of MBRL algorithm, enabling the use of the scheme with various MBRL algorithms. MBRL algorithms with $\mathcal{L}_1$ augmentation exhibit enhanced performance and sample efficiency across multiple MuJoCo environments, outperforming the original MBRL algorithms, both with and without system noise.
$\mathcal{L}_1$Quad: $\mathcal{L}_1$ Adaptive Augmentation of Geometric Control for Agile Quadrotors with Performance Guarantees
Feb 14, 2023
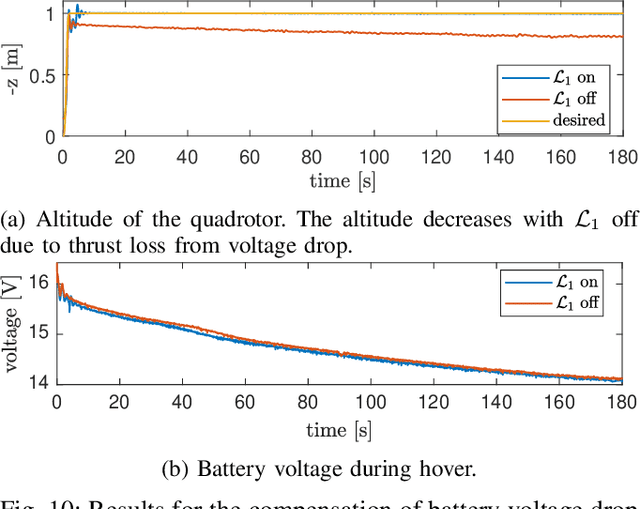

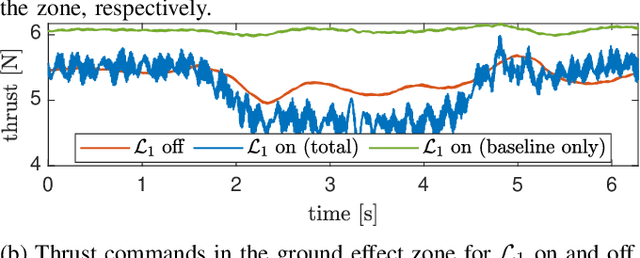
Abstract:Quadrotors that can operate safely in the presence of imperfect model knowledge and external disturbances are crucial in safety-critical applications. We present L1Quad, a control architecture for quadrotors based on the L1 adaptive control. L1Quad enables safe tubes centered around a desired trajectory that the quadrotor is always guaranteed to remain inside. Our design applies to both the rotational and the translational dynamics of the quadrotor. We lump various types of uncertainties and disturbances as unknown nonlinear (time- and state-dependent) forces and moments. Without assuming or enforcing parametric structures, L1Quad can accurately estimate and compensate for these unknown forces and moments. Extensive experimental results demonstrate that L1Quad is able to significantly outperform baseline controllers under a variety of uncertainties with consistently small tracking errors.
Guaranteed Contraction Control in the Presence of Imperfectly Learned Dynamics
Dec 15, 2021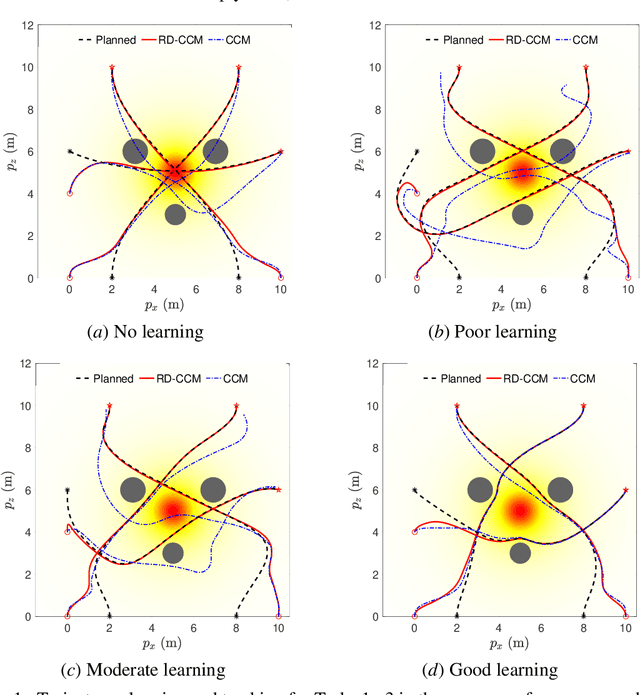
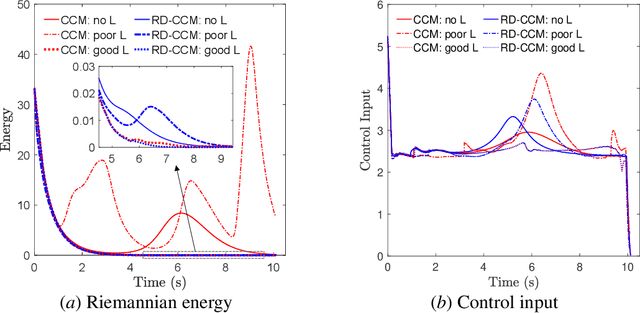
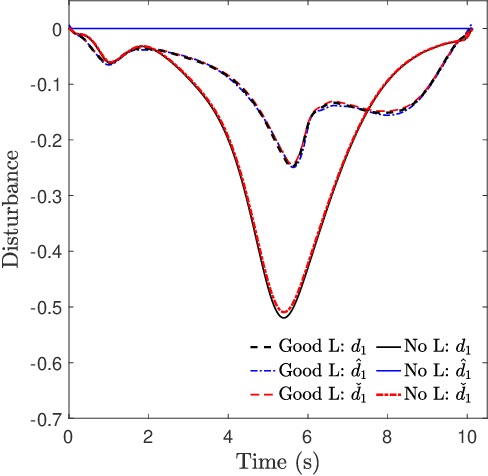
Abstract:This paper presents an approach for trajectory-centric learning control based on contraction metrics and disturbance estimation for nonlinear systems subject to matched uncertainties. The approach allows for the use of a broad class of model learning tools including deep neural networks to learn uncertain dynamics while still providing guarantees of transient tracking performance throughout the learning phase, including the special case of no learning. Within the proposed approach, a disturbance estimation law is proposed to estimate the pointwise value of the uncertainty, with pre-computable estimation error bounds (EEBs). The learned dynamics, the estimated disturbances, and the EEBs are then incorporated in a robust Riemannian energy condition to compute the control law that guarantees exponential convergence of actual trajectories to desired ones throughout the learning phase, even when the learned model is poor. On the other hand, with improved accuracy, the learned model can be incorporated in a high-level planner to plan better trajectories with improved performance, e.g., lower energy consumption and shorter travel time. The proposed framework is validated on a planar quadrotor navigation example.
Safe Sampling-Based Air-Ground Rendezvous Algorithm for Complex Urban Environments
Mar 12, 2021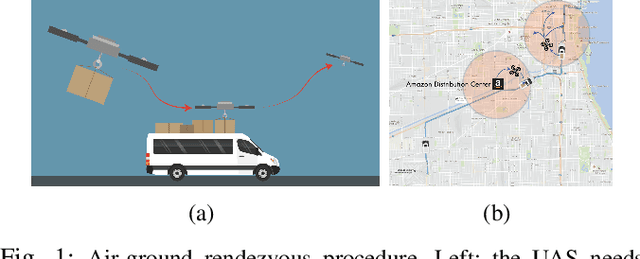
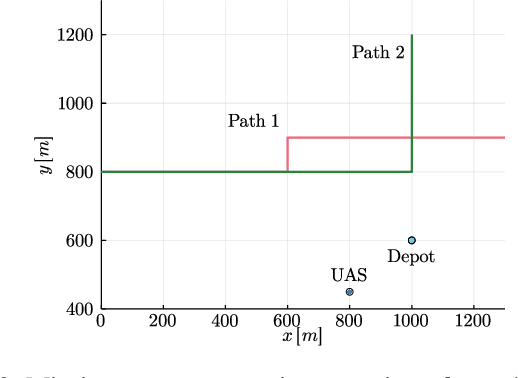
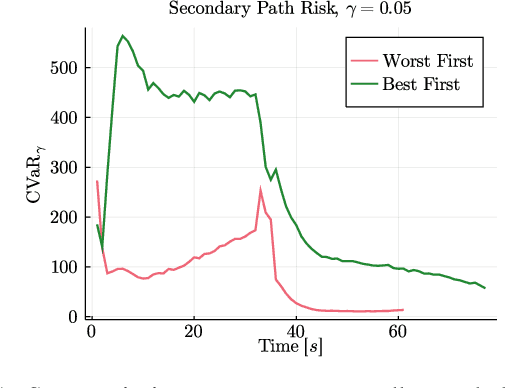
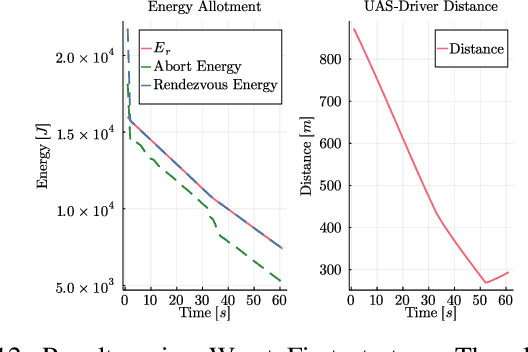
Abstract:Demand for fast and economical parcel deliveries in urban environments has risen considerably in recent years. A framework envisions efficient last-mile delivery in urban environments by leveraging a network of ride-sharing vehicles, where Unmanned Aerial Systems (UASs) drop packages on said vehicles, which then cover the majority of the distance before final aerial delivery. Notably, we consider the problem of planning a rendezvous path for the UAS to reach a human driver, who may choose between N possible paths and has uncertain behavior, while meeting strict safety constraints. The long planning horizon and safety constraints require robust heuristics that combine learning and optimal control using Gaussian Process Regression, sampling-based optimization, and Model Predictive Control. The resulting algorithm is computationally efficient and shown to be effective in a variety of qualitative scenarios.
Distributed Algorithms for Linearly-Solvable Optimal Control in Networked Multi-Agent Systems
Feb 18, 2021



Abstract:Distributed algorithms for both discrete-time and continuous-time linearly solvable optimal control (LSOC) problems of networked multi-agent systems (MASs) are investigated in this paper. A distributed framework is proposed to partition the optimal control problem of a networked MAS into several local optimal control problems in factorial subsystems, such that each (central) agent behaves optimally to minimize the joint cost function of a subsystem that comprises a central agent and its neighboring agents, and the local control actions (policies) only rely on the knowledge of local observations. Under this framework, we not only preserve the correlations between neighboring agents, but moderate the communication and computational complexities by decentralizing the sampling and computational processes over the network. For discrete-time systems modeled by Markov decision processes, the joint Bellman equation of each subsystem is transformed into a system of linear equations and solved using parallel programming. For continuous-time systems modeled by It\^o diffusion processes, the joint optimality equation of each subsystem is converted into a linear partial differential equation, whose solution is approximated by a path integral formulation and a sample-efficient relative entropy policy search algorithm, respectively. The learned control policies are generalized to solve the unlearned tasks by resorting to the compositionality principle, and illustrative examples of cooperative UAV teams are provided to verify the effectiveness and advantages of these algorithms.
Cooperative Path Integral Control for Stochastic Multi-Agent Systems
Sep 30, 2020
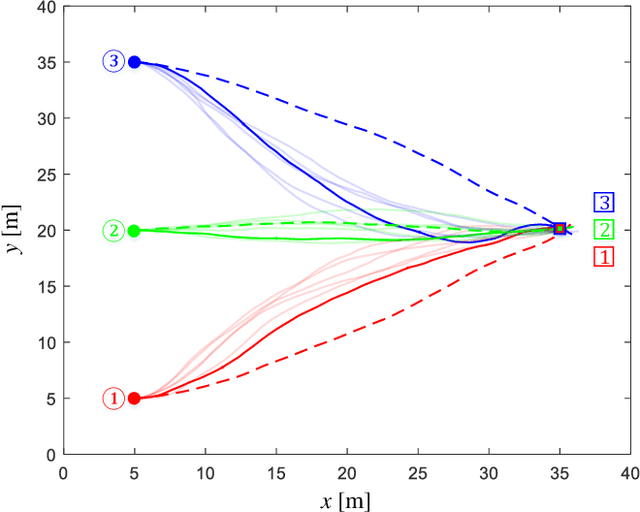

Abstract:A distributed stochastic optimal control solution is presented for cooperative multi-agent systems. The network of agents is partitioned into multiple factorial subsystems, each of which consists of a central agent and neighboring agents. Local control actions that rely only on agents' local observations are designed to optimize the joint cost functions of subsystems. When solving for the local control actions, the joint optimality equation for each subsystem is cast as a linear partial differential equation and solved using the Feynman-Kac formula. The solution and the optimal control action are then formulated as path integrals and approximated by a Monte-Carlo method. Numerical verification is provided through a simulation example consisting of a team of cooperative UAVs.
Compositionality of Linearly Solvable Optimal Control in Networked Multi-Agent Systems
Sep 28, 2020

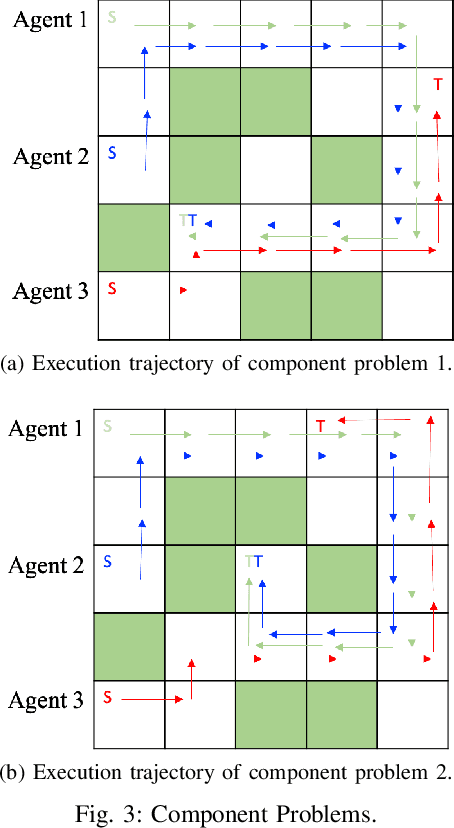

Abstract:In this paper, we discuss the methodology of generalizing the optimal control law from learned component tasks to unlearned composite tasks on Multi-Agent Systems (MASs), by using the linearity composition principle of linearly solvable optimal control (LSOC) problems. The proposed approach achieves both the compositionality and optimality of control actions simultaneously within the cooperative MAS framework in both discrete- and continuous-time in a sample-efficient manner, which reduces the burden of re-computation of the optimal control solutions for the new task on the MASs. We investigate the application of the proposed approach on the MAS with coordination between agents. The experiments show feasible results in investigated scenarios, including both discrete and continuous dynamical systems for task generalization without resampling.
$\mathcal{RL}_1$-$\mathcal{GP}$: Safe Simultaneous Learning and Control
Sep 08, 2020
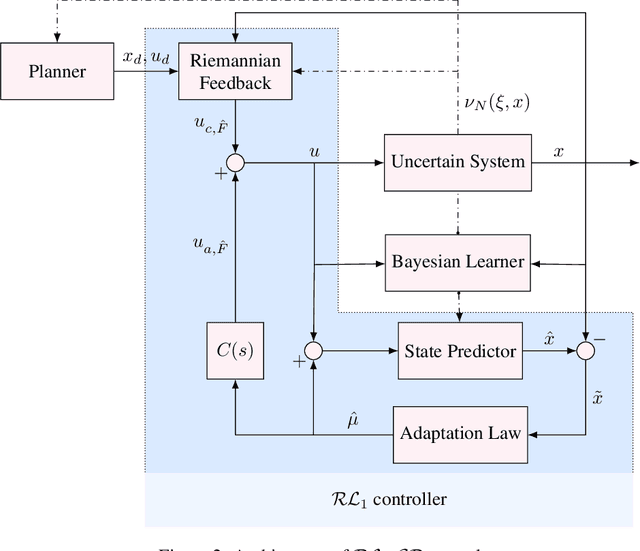
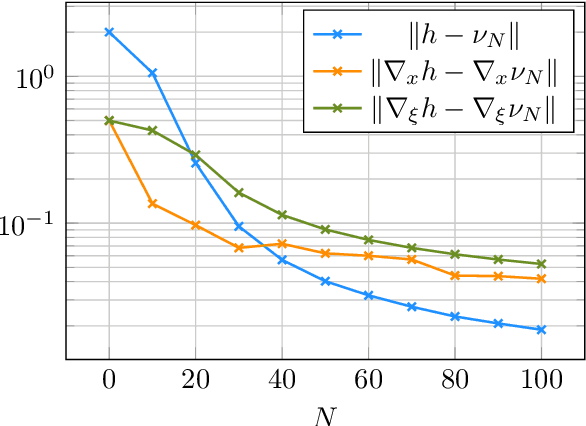
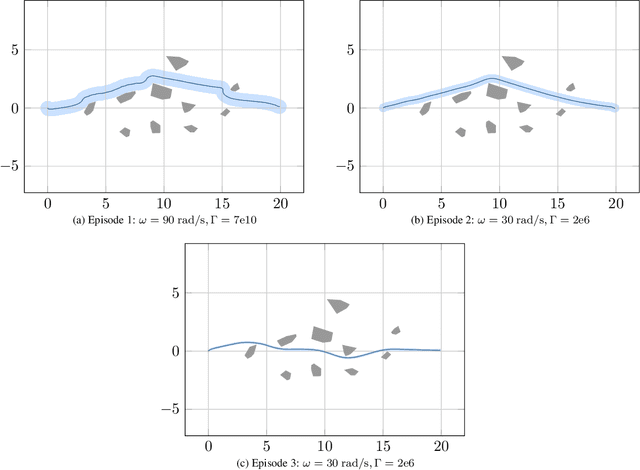
Abstract:We present $\mathcal{RL}_1$-$\mathcal{GP}$, a control framework that enables safe simultaneous learning and control for systems subject to uncertainties. The two main constituents are Riemannian energy $\mathcal{L}_1$ ($\mathcal{RL}_1$) control and Bayesian learning in the form of Gaussian process (GP) regression. The $\mathcal{RL}_1$ controller ensures that control objectives are met while providing safety certificates. Furthermore, $\mathcal{RL}_1$-$\mathcal{GP}$ incorporates any available data into a GP model of uncertainties, which improves performance and enables the motion planner to achieve optimality safely. This way, the safe operation of the system is always guaranteed, even during the learning transients. We provide a few illustrative examples for the safe learning and control of planar quadrotor systems in a variety of environments.
Safe Feedback Motion Planning: A Contraction Theory and $\mathcal{L}_1$-Adaptive Control Based Approach
Apr 02, 2020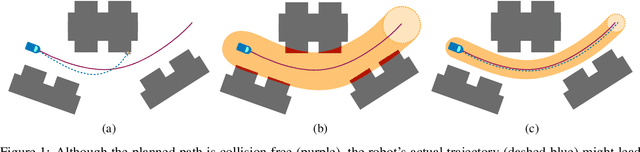
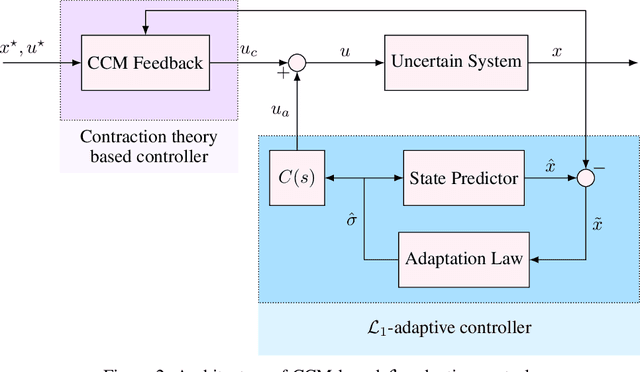
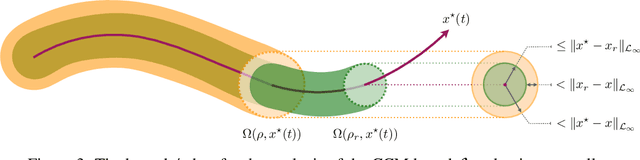
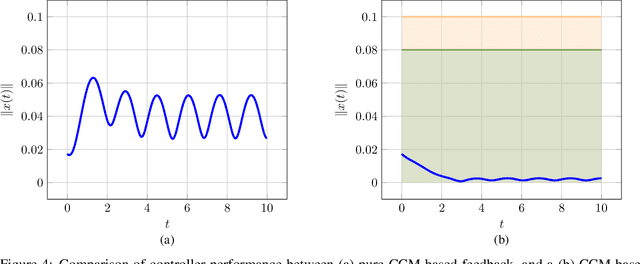
Abstract:Autonomous robots that are capable of operating safely in the presence of imperfect model knowledge or external disturbances are vital in safety-critical applications. In this paper, we present a planner-agnostic framework to design and certify safe tubes around desired trajectories that the robot is always guaranteed to remain inside of. By leveraging recent results in contraction analysis and $\mathcal{L}_1$-adaptive control we synthesize an architecture that induces safe tubes for nonlinear systems with state and time-varying uncertainties. We demonstrate with a few illustrative examples how contraction theory-based $\mathcal{L}_1$-adaptive control can be used in conjunction with traditional motion planning algorithms to obtain provably safe trajectories.
Learning Probabilistic Intersection Traffic Models for Trajectory Prediction
Feb 05, 2020



Abstract:Autonomous agents must be able to safely interact with other vehicles to integrate into urban environments. The safety of these agents is dependent on their ability to predict collisions with other vehicles' future trajectories for replanning and collision avoidance. The information needed to predict collisions can be learned from previously observed vehicle trajectories in a specific environment, generating a traffic model. The learned traffic model can then be incorporated as prior knowledge into any trajectory estimation method being used in this environment. This work presents a Gaussian process based probabilistic traffic model that is used to quantify vehicle behaviors in an intersection. The Gaussian process model provides estimates for the average vehicle trajectory, while also capturing the variance between the different paths a vehicle may take in the intersection. The method is demonstrated on a set of time-series position trajectories. These trajectories are reconstructed by removing object recognition errors and missed frames that may occur due to data source processing. To create the intersection traffic model, the reconstructed trajectories are clustered based on their source and destination lanes. For each cluster, a Gaussian process model is created to capture the average behavior and the variance of the cluster. To show the applicability of the Gaussian model, the test trajectories are classified with only partial observations. Performance is quantified by the number of observations required to correctly classify the vehicle trajectory. Both the intersection traffic modeling computations and the classification procedure are timed. These times are presented as results and demonstrate that the model can be constructed in a reasonable amount of time and the classification procedure can be used for online applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge