Distributed Algorithms for Linearly-Solvable Optimal Control in Networked Multi-Agent Systems

Distributed algorithms for both discrete-time and continuous-time linearly solvable optimal control (LSOC) problems of networked multi-agent systems (MASs) are investigated in this paper. A distributed framework is proposed to partition the optimal control problem of a networked MAS into several local optimal control problems in factorial subsystems, such that each (central) agent behaves optimally to minimize the joint cost function of a subsystem that comprises a central agent and its neighboring agents, and the local control actions (policies) only rely on the knowledge of local observations. Under this framework, we not only preserve the correlations between neighboring agents, but moderate the communication and computational complexities by decentralizing the sampling and computational processes over the network. For discrete-time systems modeled by Markov decision processes, the joint Bellman equation of each subsystem is transformed into a system of linear equations and solved using parallel programming. For continuous-time systems modeled by It\^o diffusion processes, the joint optimality equation of each subsystem is converted into a linear partial differential equation, whose solution is approximated by a path integral formulation and a sample-efficient relative entropy policy search algorithm, respectively. The learned control policies are generalized to solve the unlearned tasks by resorting to the compositionality principle, and illustrative examples of cooperative UAV teams are provided to verify the effectiveness and advantages of these algorithms.

Cooperative Path Integral Control for Stochastic Multi-Agent Systems

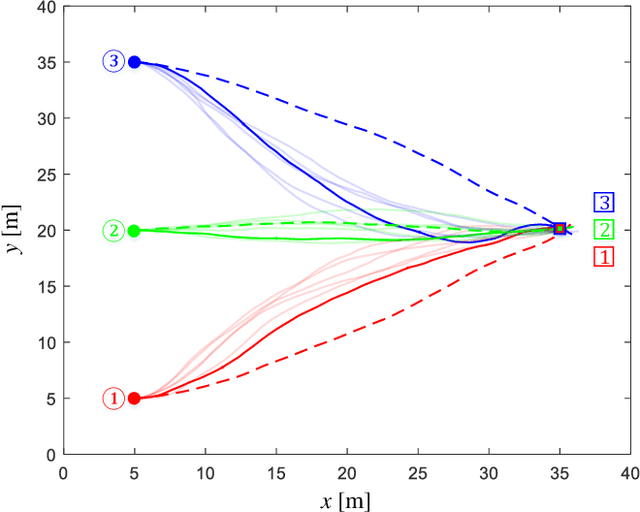
A distributed stochastic optimal control solution is presented for cooperative multi-agent systems. The network of agents is partitioned into multiple factorial subsystems, each of which consists of a central agent and neighboring agents. Local control actions that rely only on agents' local observations are designed to optimize the joint cost functions of subsystems. When solving for the local control actions, the joint optimality equation for each subsystem is cast as a linear partial differential equation and solved using the Feynman-Kac formula. The solution and the optimal control action are then formulated as path integrals and approximated by a Monte-Carlo method. Numerical verification is provided through a simulation example consisting of a team of cooperative UAVs.

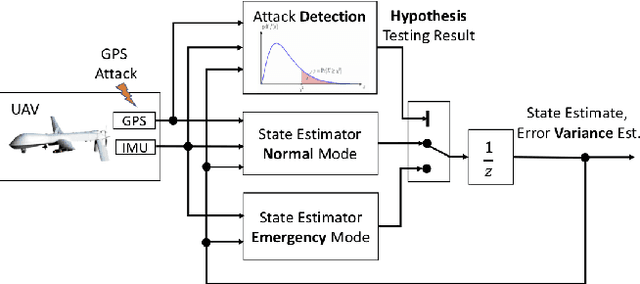
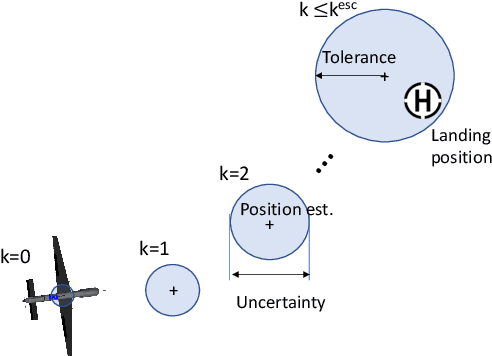
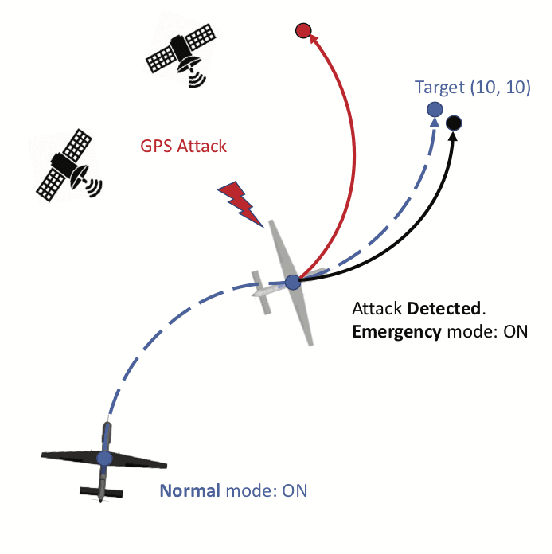
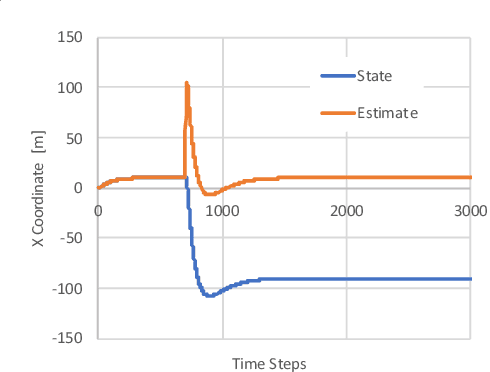
Towards Resilient UAV: Escape Time in GPS Denied Environment with Sensor Drift

This paper considers a resilient state estimation framework for unmanned aerial vehicles (UAVs) that integrates a Kalman filter-like state estimator and an attack detector. When an attack is detected, the state estimator uses only IMU signals as the GPS signals do not contain legitimate information. This limited sensor availability induces a sensor drift problem questioning the reliability of the sensor estimates. We propose a new resilience measure, escape time, as the safe time within which the estimation errors remain in a tolerable region with high probability. This paper analyzes the stability of the proposed resilient estimation framework and quantifies a lower bound for the escape time. Moreover, simulations of the UAV model demonstrate the performance of the proposed framework and provide analytical results.

Target Assignment in Robotic Networks: Distance Optimality Guarantees and Hierarchical Strategies

We study the problem of multi-robot target assignment to minimize the total distance traveled by the robots until they all reach an equal number of static targets. In the first half of the paper, we present a necessary and sufficient condition under which true distance optimality can be achieved for robots with limited communication and target-sensing ranges. Moreover, we provide an explicit, non-asymptotic formula for computing the number of robots needed to achieve distance optimality in terms of the robots' communication and target-sensing ranges with arbitrary guaranteed probabilities. The same bounds are also shown to be asymptotically tight. In the second half of the paper, we present suboptimal strategies for use when the number of robots cannot be chosen freely. Assuming first that all targets are known to all robots, we employ a hierarchical communication model in which robots communicate only with other robots in the same partitioned region. This hierarchical communication model leads to constant approximations of true distance-optimal solutions under mild assumptions. We then revisit the limited communication and sensing models. By combining simple rendezvous-based strategies with a hierarchical communication model, we obtain decentralized hierarchical strategies that achieve constant approximation ratios with respect to true distance optimality. Results of simulation show that the approximation ratio is as low as 1.4.