Cooperative Path Integral Control for Stochastic Multi-Agent Systems
Paper and Code
Sep 30, 2020
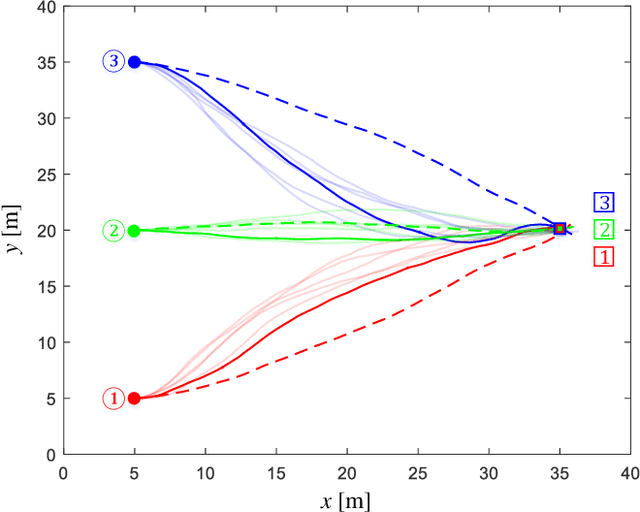

A distributed stochastic optimal control solution is presented for cooperative multi-agent systems. The network of agents is partitioned into multiple factorial subsystems, each of which consists of a central agent and neighboring agents. Local control actions that rely only on agents' local observations are designed to optimize the joint cost functions of subsystems. When solving for the local control actions, the joint optimality equation for each subsystem is cast as a linear partial differential equation and solved using the Feynman-Kac formula. The solution and the optimal control action are then formulated as path integrals and approximated by a Monte-Carlo method. Numerical verification is provided through a simulation example consisting of a team of cooperative UAVs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge