Neng Wan
Transformers for prompt-level EMA non-response prediction
Nov 01, 2021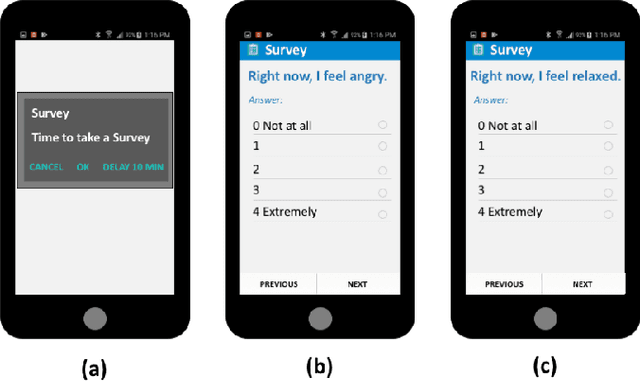
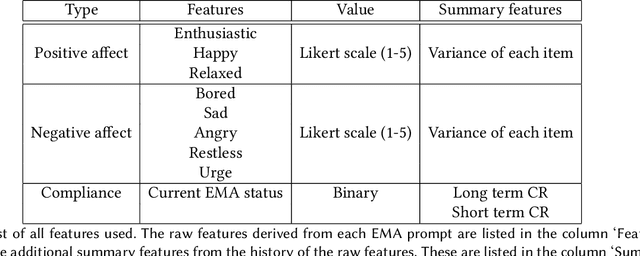
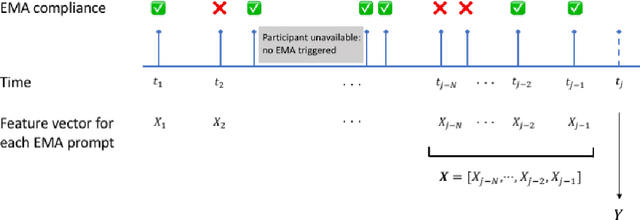

Abstract:Ecological Momentary Assessments (EMAs) are an important psychological data source for measuring current cognitive states, affect, behavior, and environmental factors from participants in mobile health (mHealth) studies and treatment programs. Non-response, in which participants fail to respond to EMA prompts, is an endemic problem. The ability to accurately predict non-response could be utilized to improve EMA delivery and develop compliance interventions. Prior work has explored classical machine learning models for predicting non-response. However, as increasingly large EMA datasets become available, there is the potential to leverage deep learning models that have been effective in other fields. Recently, transformer models have shown state-of-the-art performance in NLP and other domains. This work is the first to explore the use of transformers for EMA data analysis. We address three key questions in applying transformers to EMA data: 1. Input representation, 2. encoding temporal information, 3. utility of pre-training on improving downstream prediction task performance. The transformer model achieves a non-response prediction AUC of 0.77 and is significantly better than classical ML and LSTM-based deep learning models. We will make our a predictive model trained on a corpus of 40K EMA samples freely-available to the research community, in order to facilitate the development of future transformer-based EMA analysis works.
Distributed Algorithms for Linearly-Solvable Optimal Control in Networked Multi-Agent Systems
Feb 18, 2021



Abstract:Distributed algorithms for both discrete-time and continuous-time linearly solvable optimal control (LSOC) problems of networked multi-agent systems (MASs) are investigated in this paper. A distributed framework is proposed to partition the optimal control problem of a networked MAS into several local optimal control problems in factorial subsystems, such that each (central) agent behaves optimally to minimize the joint cost function of a subsystem that comprises a central agent and its neighboring agents, and the local control actions (policies) only rely on the knowledge of local observations. Under this framework, we not only preserve the correlations between neighboring agents, but moderate the communication and computational complexities by decentralizing the sampling and computational processes over the network. For discrete-time systems modeled by Markov decision processes, the joint Bellman equation of each subsystem is transformed into a system of linear equations and solved using parallel programming. For continuous-time systems modeled by It\^o diffusion processes, the joint optimality equation of each subsystem is converted into a linear partial differential equation, whose solution is approximated by a path integral formulation and a sample-efficient relative entropy policy search algorithm, respectively. The learned control policies are generalized to solve the unlearned tasks by resorting to the compositionality principle, and illustrative examples of cooperative UAV teams are provided to verify the effectiveness and advantages of these algorithms.
$f$-Divergence Variational Inference
Oct 20, 2020



Abstract:This paper introduces the $f$-divergence variational inference ($f$-VI) that generalizes variational inference to all $f$-divergences. Initiated from minimizing a crafty surrogate $f$-divergence that shares the statistical consistency with the $f$-divergence, the $f$-VI framework not only unifies a number of existing VI methods, e.g. Kullback-Leibler VI, R\'{e}nyi's $\alpha$-VI, and $\chi$-VI, but offers a standardized toolkit for VI subject to arbitrary divergences from $f$-divergence family. A general $f$-variational bound is derived and provides a sandwich estimate of marginal likelihood (or evidence). The development of the $f$-VI unfolds with a stochastic optimization scheme that utilizes the reparameterization trick, importance weighting and Monte Carlo approximation; a mean-field approximation scheme that generalizes the well-known coordinate ascent variational inference (CAVI) is also proposed for $f$-VI. Empirical examples, including variational autoencoders and Bayesian neural networks, are provided to demonstrate the effectiveness and the wide applicability of $f$-VI.
Cooperative Path Integral Control for Stochastic Multi-Agent Systems
Sep 30, 2020
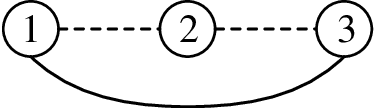
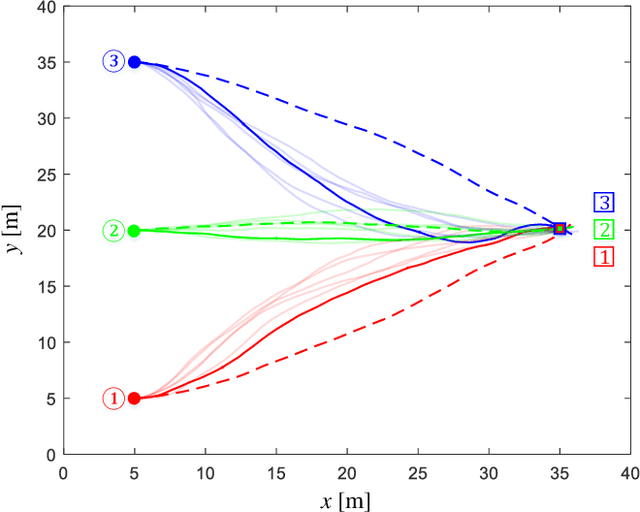

Abstract:A distributed stochastic optimal control solution is presented for cooperative multi-agent systems. The network of agents is partitioned into multiple factorial subsystems, each of which consists of a central agent and neighboring agents. Local control actions that rely only on agents' local observations are designed to optimize the joint cost functions of subsystems. When solving for the local control actions, the joint optimality equation for each subsystem is cast as a linear partial differential equation and solved using the Feynman-Kac formula. The solution and the optimal control action are then formulated as path integrals and approximated by a Monte-Carlo method. Numerical verification is provided through a simulation example consisting of a team of cooperative UAVs.
Compositionality of Linearly Solvable Optimal Control in Networked Multi-Agent Systems
Sep 28, 2020

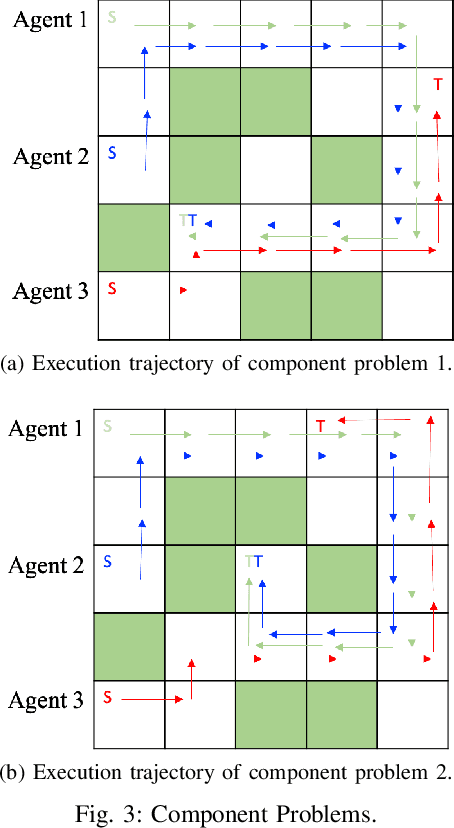

Abstract:In this paper, we discuss the methodology of generalizing the optimal control law from learned component tasks to unlearned composite tasks on Multi-Agent Systems (MASs), by using the linearity composition principle of linearly solvable optimal control (LSOC) problems. The proposed approach achieves both the compositionality and optimality of control actions simultaneously within the cooperative MAS framework in both discrete- and continuous-time in a sample-efficient manner, which reduces the burden of re-computation of the optimal control solutions for the new task on the MASs. We investigate the application of the proposed approach on the MAS with coordination between agents. The experiments show feasible results in investigated scenarios, including both discrete and continuous dynamical systems for task generalization without resampling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge