Cho Lam
Transformers for prompt-level EMA non-response prediction
Nov 01, 2021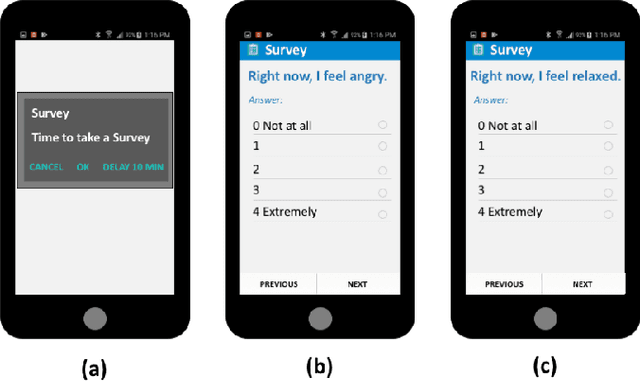
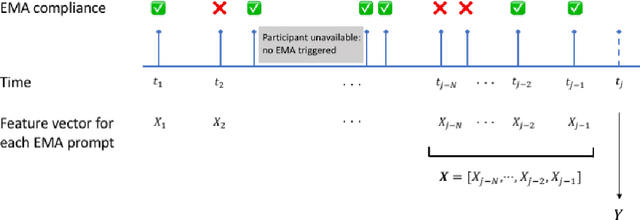

Abstract:Ecological Momentary Assessments (EMAs) are an important psychological data source for measuring current cognitive states, affect, behavior, and environmental factors from participants in mobile health (mHealth) studies and treatment programs. Non-response, in which participants fail to respond to EMA prompts, is an endemic problem. The ability to accurately predict non-response could be utilized to improve EMA delivery and develop compliance interventions. Prior work has explored classical machine learning models for predicting non-response. However, as increasingly large EMA datasets become available, there is the potential to leverage deep learning models that have been effective in other fields. Recently, transformer models have shown state-of-the-art performance in NLP and other domains. This work is the first to explore the use of transformers for EMA data analysis. We address three key questions in applying transformers to EMA data: 1. Input representation, 2. encoding temporal information, 3. utility of pre-training on improving downstream prediction task performance. The transformer model achieves a non-response prediction AUC of 0.77 and is significantly better than classical ML and LSTM-based deep learning models. We will make our a predictive model trained on a corpus of 40K EMA samples freely-available to the research community, in order to facilitate the development of future transformer-based EMA analysis works.
A Functional EM Algorithm for Panel Count Data with Missing Counts
Mar 28, 2020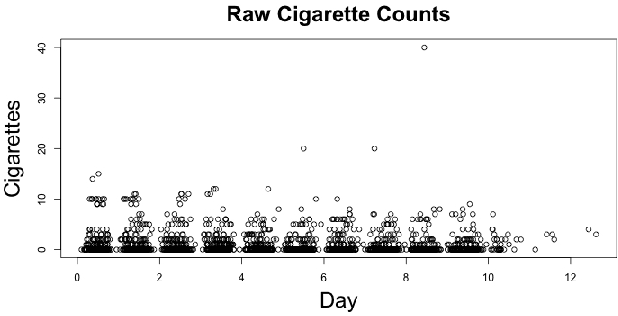
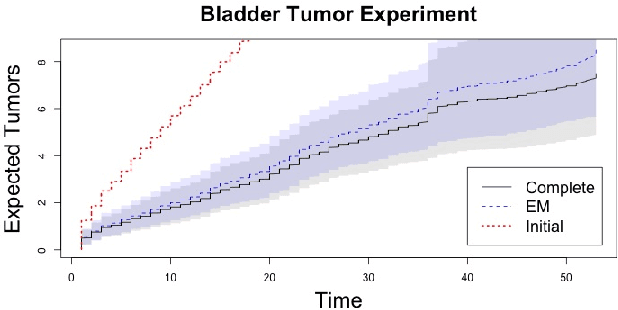
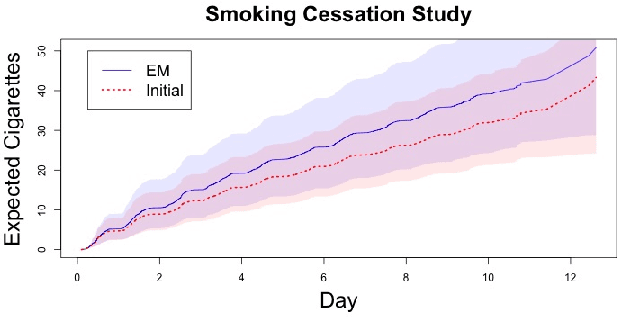
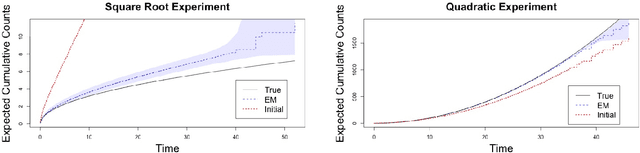
Abstract:Panel count data is recurrent events data where counts of events are observed at discrete time points. Panel counts naturally describe self-reported behavioral data, and the occurrence of missing or unreliable reports is common. Unfortunately, no prior work has tackled the problem of missingness in this setting. We address this gap in the literature by developing a novel functional EM algorithm that can be used as a wrapper around several popular panel count mean function inference methods when some counts are missing. We provide a novel theoretical analysis of our method showing strong consistency. Extending the methods in (Balakrishnan et al., 2017, Wu et al. 2016), we show that the functional EM algorithm recovers the true mean function of the counting process. We accomplish this by developing alternative regularity conditions for our objective function in order to show convergence of the population EM algorithm. We prove strong consistency of the M-step, thus giving strong consistency guarantees for the finite sample EM algorithm. We present experimental results for synthetic data, synthetic missingness on real data, and a smoking cessation study, where we find that participants may underestimate cigarettes smoked by approximately 18.6% over a 12 day period.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge