A Functional EM Algorithm for Panel Count Data with Missing Counts

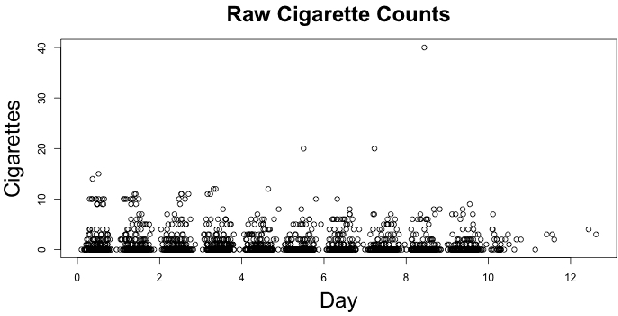
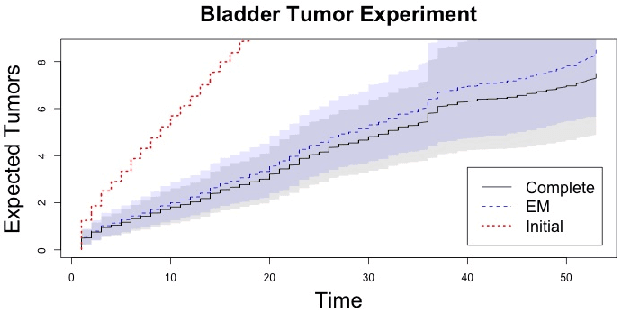
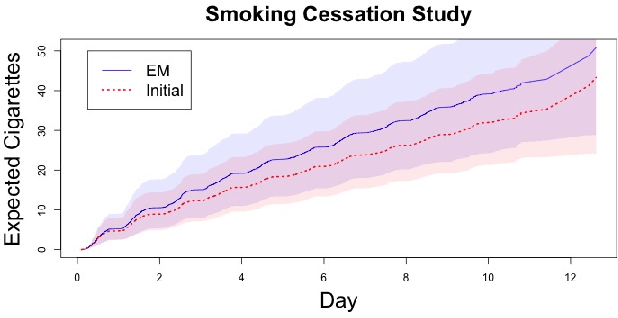
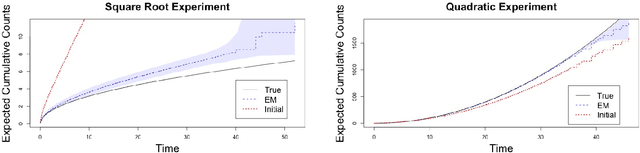
Panel count data is recurrent events data where counts of events are observed at discrete time points. Panel counts naturally describe self-reported behavioral data, and the occurrence of missing or unreliable reports is common. Unfortunately, no prior work has tackled the problem of missingness in this setting. We address this gap in the literature by developing a novel functional EM algorithm that can be used as a wrapper around several popular panel count mean function inference methods when some counts are missing. We provide a novel theoretical analysis of our method showing strong consistency. Extending the methods in (Balakrishnan et al., 2017, Wu et al. 2016), we show that the functional EM algorithm recovers the true mean function of the counting process. We accomplish this by developing alternative regularity conditions for our objective function in order to show convergence of the population EM algorithm. We prove strong consistency of the M-step, thus giving strong consistency guarantees for the finite sample EM algorithm. We present experimental results for synthetic data, synthetic missingness on real data, and a smoking cessation study, where we find that participants may underestimate cigarettes smoked by approximately 18.6% over a 12 day period.