Selective Inference for Time-Varying Effect Moderation

Causal effect moderation investigates how the effect of interventions (or treatments) on outcome variables changes based on observed characteristics of individuals, known as potential effect moderators. With advances in data collection, datasets containing many observed features as potential moderators have become increasingly common. High-dimensional analyses often lack interpretability, with important moderators masked by noise, while low-dimensional, marginal analyses yield many false positives due to strong correlations with true moderators. In this paper, we propose a two-step method for selective inference on time-varying causal effect moderation that addresses the limitations of both high-dimensional and marginal analyses. Our method first selects a relatively smaller, more interpretable model to estimate a linear causal effect moderation using a Gaussian randomization approach. We then condition on the selection event to construct a pivot, enabling uniformly asymptotic semi-parametric inference in the selected model. Through simulations and real data analyses, we show that our method consistently achieves valid coverage rates, even when existing conditional methods and common sample splitting techniques fail. Moreover, our method yields shorter, bounded intervals, unlike existing methods that may produce infinitely long intervals.

Non-Stationary Latent Auto-Regressive Bandits

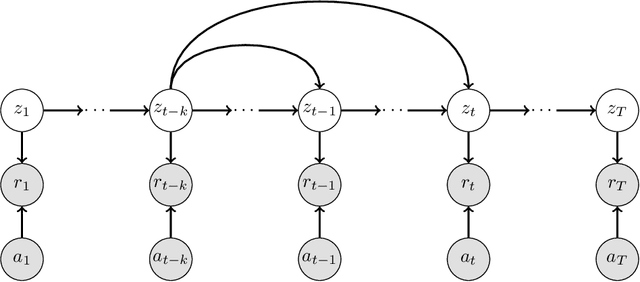
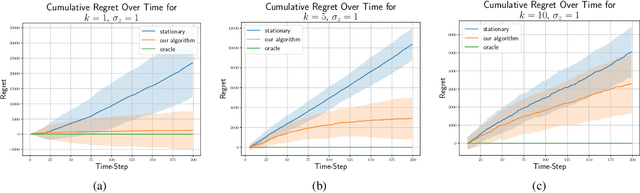
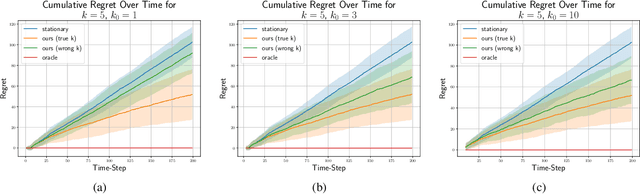
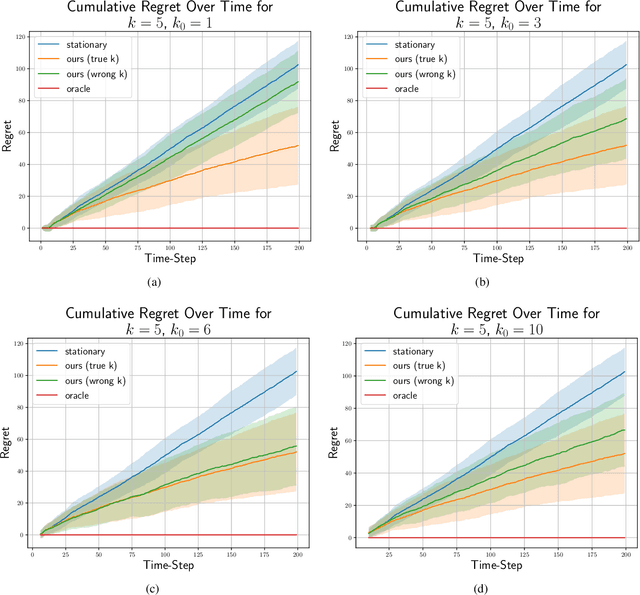
We consider the stochastic multi-armed bandit problem with non-stationary rewards. We present a novel formulation of non-stationarity in the environment where changes in the mean reward of the arms over time are due to some unknown, latent, auto-regressive (AR) state of order $k$. We call this new environment the latent AR bandit. Different forms of the latent AR bandit appear in many real-world settings, especially in emerging scientific fields such as behavioral health or education where there are few mechanistic models of the environment. If the AR order $k$ is known, we propose an algorithm that achieves $\tilde{O}(k\sqrt{T})$ regret in this setting. Empirically, our algorithm outperforms standard UCB across multiple non-stationary environments, even if $k$ is mis-specified.

A Meta-Learning Method for Estimation of Causal Excursion Effects to Assess Time-Varying Moderation

Twin revolutions in wearable technologies and smartphone-delivered digital health interventions have significantly expanded the accessibility and uptake of mobile health (mHealth) interventions across various health science domains. Sequentially randomized experiments called micro-randomized trials (MRTs) have grown in popularity to empirically evaluate the effectiveness of these mHealth intervention components. MRTs have given rise to a new class of causal estimands known as "causal excursion effects", which enable health scientists to assess how intervention effectiveness changes over time or is moderated by individual characteristics, context, or responses in the past. However, current data analysis methods for estimating causal excursion effects require pre-specified features of the observed high-dimensional history to construct a working model of an important nuisance parameter. While machine learning algorithms are ideal for automatic feature construction, their naive application to causal excursion estimation can lead to bias under model misspecification, potentially yielding incorrect conclusions about intervention effectiveness. To address this issue, this paper revisits the estimation of causal excursion effects from a meta-learner perspective, where the analyst remains agnostic to the choices of supervised learning algorithms used to estimate nuisance parameters. The paper presents asymptotic properties of the novel estimators and compares them theoretically and through extensive simulation experiments, demonstrating relative efficiency gains and supporting the recommendation for a doubly robust alternative to existing methods. Finally, the practical utility of the proposed methods is demonstrated by analyzing data from a multi-institution cohort of first-year medical residents in the United States (NeCamp et al., 2020).

Kernel Deformed Exponential Families for Sparse Continuous Attention

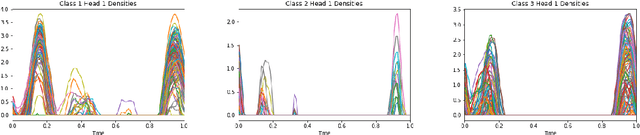
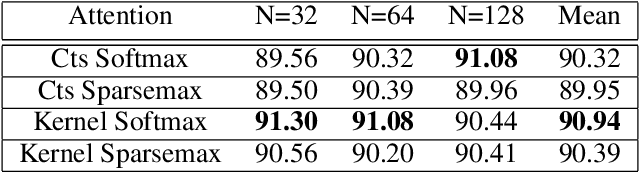
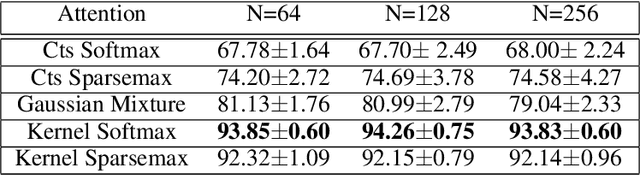
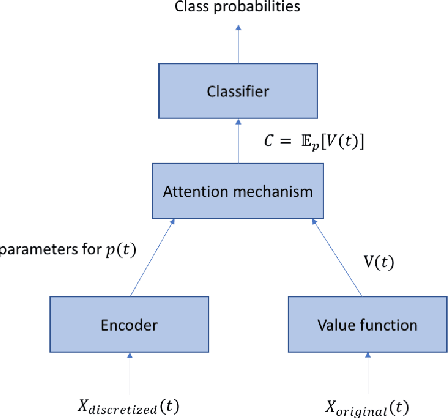
Attention mechanisms take an expectation of a data representation with respect to probability weights. This creates summary statistics that focus on important features. Recently, (Martins et al. 2020, 2021) proposed continuous attention mechanisms, focusing on unimodal attention densities from the exponential and deformed exponential families: the latter has sparse support. (Farinhas et al. 2021) extended this to use Gaussian mixture attention densities, which are a flexible class with dense support. In this paper, we extend this to two general flexible classes: kernel exponential families and our new sparse counterpart kernel deformed exponential families. Theoretically, we show new existence results for both kernel exponential and deformed exponential families, and that the deformed case has similar approximation capabilities to kernel exponential families. Experiments show that kernel deformed exponential families can attend to multiple compact regions of the data domain.

A Functional EM Algorithm for Panel Count Data with Missing Counts

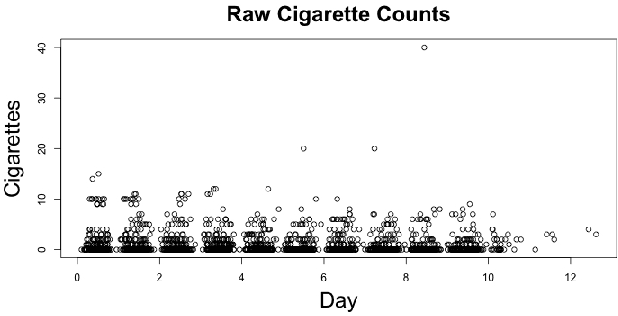
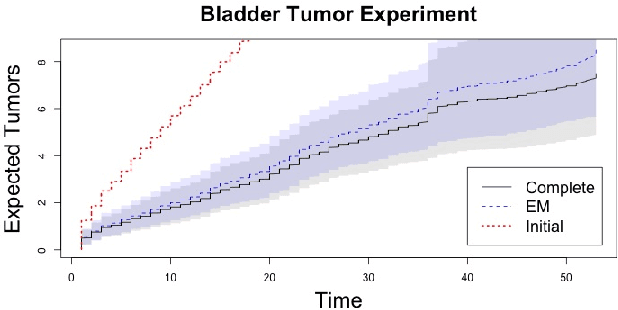
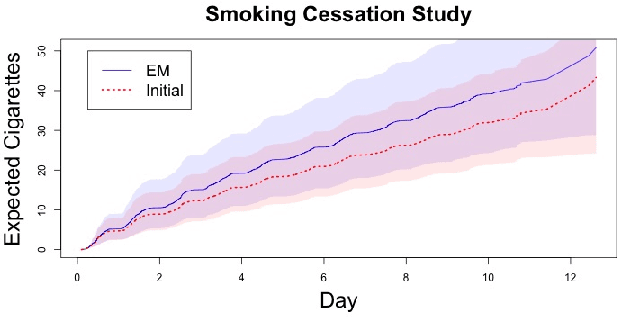
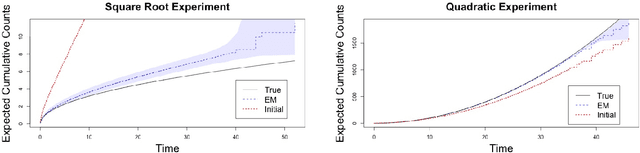
Panel count data is recurrent events data where counts of events are observed at discrete time points. Panel counts naturally describe self-reported behavioral data, and the occurrence of missing or unreliable reports is common. Unfortunately, no prior work has tackled the problem of missingness in this setting. We address this gap in the literature by developing a novel functional EM algorithm that can be used as a wrapper around several popular panel count mean function inference methods when some counts are missing. We provide a novel theoretical analysis of our method showing strong consistency. Extending the methods in (Balakrishnan et al., 2017, Wu et al. 2016), we show that the functional EM algorithm recovers the true mean function of the counting process. We accomplish this by developing alternative regularity conditions for our objective function in order to show convergence of the population EM algorithm. We prove strong consistency of the M-step, thus giving strong consistency guarantees for the finite sample EM algorithm. We present experimental results for synthetic data, synthetic missingness on real data, and a smoking cessation study, where we find that participants may underestimate cigarettes smoked by approximately 18.6% over a 12 day period.