Kernel Deformed Exponential Families for Sparse Continuous Attention
Paper and Code
Nov 12, 2021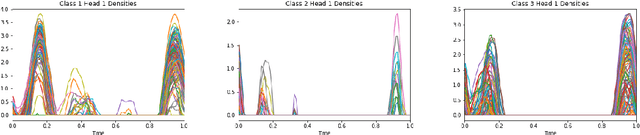
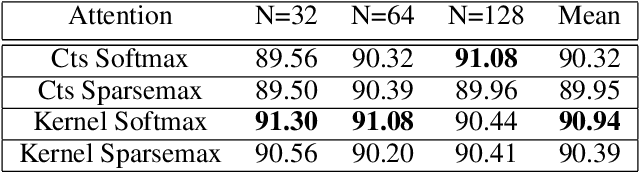
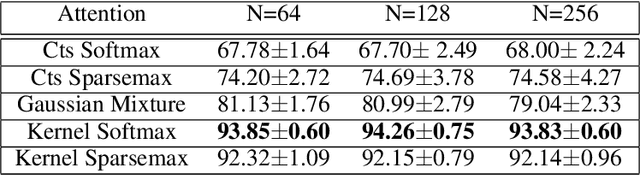
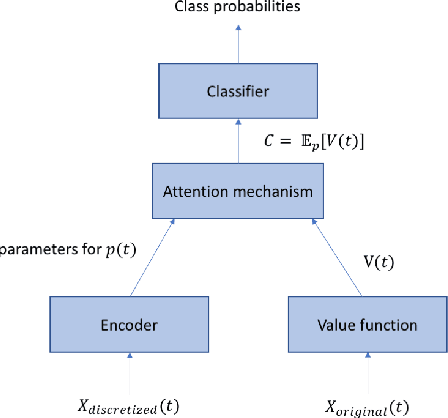
Attention mechanisms take an expectation of a data representation with respect to probability weights. This creates summary statistics that focus on important features. Recently, (Martins et al. 2020, 2021) proposed continuous attention mechanisms, focusing on unimodal attention densities from the exponential and deformed exponential families: the latter has sparse support. (Farinhas et al. 2021) extended this to use Gaussian mixture attention densities, which are a flexible class with dense support. In this paper, we extend this to two general flexible classes: kernel exponential families and our new sparse counterpart kernel deformed exponential families. Theoretically, we show new existence results for both kernel exponential and deformed exponential families, and that the deformed case has similar approximation capabilities to kernel exponential families. Experiments show that kernel deformed exponential families can attend to multiple compact regions of the data domain.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge