K2-Think: A Parameter-Efficient Reasoning System

K2-Think is a reasoning system that achieves state-of-the-art performance with a 32B parameter model, matching or surpassing much larger models like GPT-OSS 120B and DeepSeek v3.1. Built on the Qwen2.5 base model, our system shows that smaller models can compete at the highest levels by combining advanced post-training and test-time computation techniques. The approach is based on six key technical pillars: Long Chain-of-thought Supervised Finetuning, Reinforcement Learning with Verifiable Rewards (RLVR), Agentic planning prior to reasoning, Test-time Scaling, Speculative Decoding, and Inference-optimized Hardware, all using publicly available open-source datasets. K2-Think excels in mathematical reasoning, achieving state-of-the-art scores on public benchmarks for open-source models, while also performing strongly in other areas such as Code and Science. Our results confirm that a more parameter-efficient model like K2-Think 32B can compete with state-of-the-art systems through an integrated post-training recipe that includes long chain-of-thought training and strategic inference-time enhancements, making open-source reasoning systems more accessible and affordable. K2-Think is freely available at k2think.ai, offering best-in-class inference speeds of over 2,000 tokens per second per request via the Cerebras Wafer-Scale Engine.

PyPulse: A Python Library for Biosignal Imputation

We introduce PyPulse, a Python package for imputation of biosignals in both clinical and wearable sensor settings. Missingness is commonplace in these settings and can arise from multiple causes, such as insecure sensor attachment or data transmission loss. PyPulse's framework provides a modular and extendable framework with high ease-of-use for a broad userbase, including non-machine-learning bioresearchers. Specifically, its new capabilities include using pre-trained imputation methods out-of-the-box on custom datasets, running the full workflow of training or testing a baseline method with a single line of code, and comparing baseline methods in an interactive visualization tool. We released PyPulse under the MIT License on Github and PyPI. The source code can be found at: https://github.com/rehg-lab/pulseimpute.

Debiased Machine Learning and Network Cohesion for Doubly-Robust Differential Reward Models in Contextual Bandits

A common approach to learning mobile health (mHealth) intervention policies is linear Thompson sampling. Two desirable mHealth policy features are (1) pooling information across individuals and time and (2) incorporating a time-varying baseline reward. Previous approaches pooled information across individuals but not time, failing to capture trends in treatment effects over time. In addition, these approaches did not explicitly model the baseline reward, which limited the ability to precisely estimate the parameters in the differential reward model. In this paper, we propose a novel Thompson sampling algorithm, termed ''DML-TS-NNR'' that leverages (1) nearest-neighbors to efficiently pool information on the differential reward function across users and time and (2) the Double Machine Learning (DML) framework to explicitly model baseline rewards and stay agnostic to the supervised learning algorithms used. By explicitly modeling baseline rewards, we obtain smaller confidence sets for the differential reward parameters. We offer theoretical guarantees on the pseudo-regret, which are supported by empirical results. Importantly, the DML-TS-NNR algorithm demonstrates robustness to potential misspecifications in the baseline reward model.

Retrieval-Based Reconstruction For Time-series Contrastive Learning

The success of self-supervised contrastive learning hinges on identifying positive data pairs that, when pushed together in embedding space, encode useful information for subsequent downstream tasks. However, in time-series, this is challenging because creating positive pairs via augmentations may break the original semantic meaning. We hypothesize that if we can retrieve information from one subsequence to successfully reconstruct another subsequence, then they should form a positive pair. Harnessing this intuition, we introduce our novel approach: REtrieval-BAsed Reconstruction (REBAR) contrastive learning. First, we utilize a convolutional cross-attention architecture to calculate the REBAR error between two different time-series. Then, through validation experiments, we show that the REBAR error is a predictor of mutual class membership, justifying its usage as a positive/negative labeler. Finally, once integrated into a contrastive learning framework, our REBAR method can learn an embedding that achieves state-of-the-art performance on downstream tasks across various modalities.

KrADagrad: Kronecker Approximation-Domination Gradient Preconditioned Stochastic Optimization

Second order stochastic optimizers allow parameter update step size and direction to adapt to loss curvature, but have traditionally required too much memory and compute for deep learning. Recently, Shampoo [Gupta et al., 2018] introduced a Kronecker factored preconditioner to reduce these requirements: it is used for large deep models [Anil et al., 2020] and in production [Anil et al., 2022]. However, it takes inverse matrix roots of ill-conditioned matrices. This requires 64-bit precision, imposing strong hardware constraints. In this paper, we propose a novel factorization, Kronecker Approximation-Domination (KrAD). Using KrAD, we update a matrix that directly approximates the inverse empirical Fisher matrix (like full matrix AdaGrad), avoiding inversion and hence 64-bit precision. We then propose KrADagrad$^\star$, with similar computational costs to Shampoo and the same regret. Synthetic ill-conditioned experiments show improved performance over Shampoo for 32-bit precision, while for several real datasets we have comparable or better generalization.

SKI to go Faster: Accelerating Toeplitz Neural Networks via Asymmetric Kernels

Toeplitz Neural Networks (TNNs) (Qin et. al. 2023) are a recent sequence model with impressive results. They require O(n log n) computational complexity and O(n) relative positional encoder (RPE) multi-layer perceptron (MLP) and decay bias calls. We aim to reduce both. We first note that the RPE is a non-SPD (symmetric positive definite) kernel and the Toeplitz matrices are pseudo-Gram matrices. Further 1) the learned kernels display spiky behavior near the main diagonals with otherwise smooth behavior; 2) the RPE MLP is slow. For bidirectional models, this motivates a sparse plus low-rank Toeplitz matrix decomposition. For the sparse component's action, we do a small 1D convolution. For the low rank component, we replace the RPE MLP with linear interpolation and use asymmetric Structured Kernel Interpolation (SKI) (Wilson et. al. 2015) for O(n) complexity: we provide rigorous error analysis. For causal models, "fast" causal masking (Katharopoulos et. al. 2020) negates SKI's benefits. Working in the frequency domain, we avoid an explicit decay bias. To enforce causality, we represent the kernel via the real part of its frequency response using the RPE and compute the imaginary part via a Hilbert transform. This maintains O(n log n) complexity but achieves an absolute speedup. Modeling the frequency response directly is also competitive for bidirectional training, using one fewer FFT. We set a speed state of the art on Long Range Arena (Tay et. al. 2020) with minimal score degradation.

PulseImpute: A Novel Benchmark Task for Pulsative Physiological Signal Imputation

The promise of Mobile Health (mHealth) is the ability to use wearable sensors to monitor participant physiology at high frequencies during daily life to enable temporally-precise health interventions. However, a major challenge is frequent missing data. Despite a rich imputation literature, existing techniques are ineffective for the pulsative signals which comprise many mHealth applications, and a lack of available datasets has stymied progress. We address this gap with PulseImpute, the first large-scale pulsative signal imputation challenge which includes realistic mHealth missingness models, an extensive set of baselines, and clinically-relevant downstream tasks. Our baseline models include a novel transformer-based architecture designed to exploit the structure of pulsative signals. We hope that PulseImpute will enable the ML community to tackle this significant and challenging task.

Kernel Deformed Exponential Families for Sparse Continuous Attention

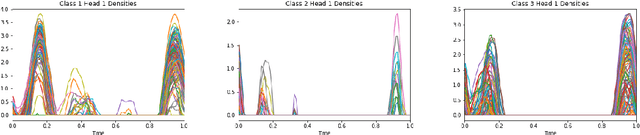
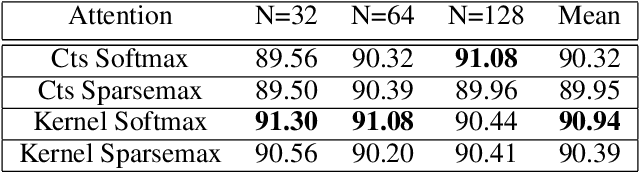
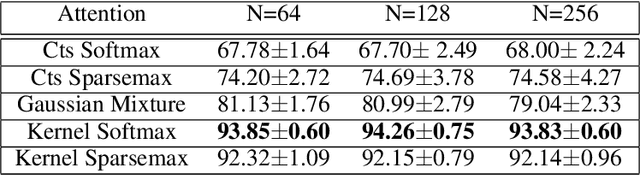
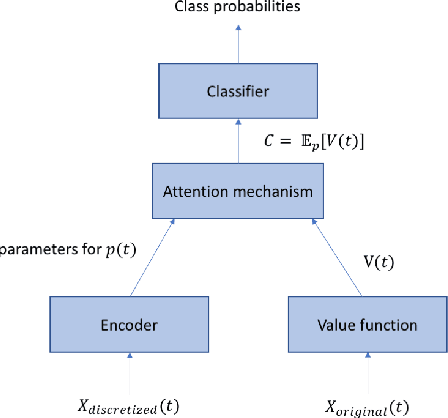
Attention mechanisms take an expectation of a data representation with respect to probability weights. This creates summary statistics that focus on important features. Recently, (Martins et al. 2020, 2021) proposed continuous attention mechanisms, focusing on unimodal attention densities from the exponential and deformed exponential families: the latter has sparse support. (Farinhas et al. 2021) extended this to use Gaussian mixture attention densities, which are a flexible class with dense support. In this paper, we extend this to two general flexible classes: kernel exponential families and our new sparse counterpart kernel deformed exponential families. Theoretically, we show new existence results for both kernel exponential and deformed exponential families, and that the deformed case has similar approximation capabilities to kernel exponential families. Experiments show that kernel deformed exponential families can attend to multiple compact regions of the data domain.

Transformers for prompt-level EMA non-response prediction

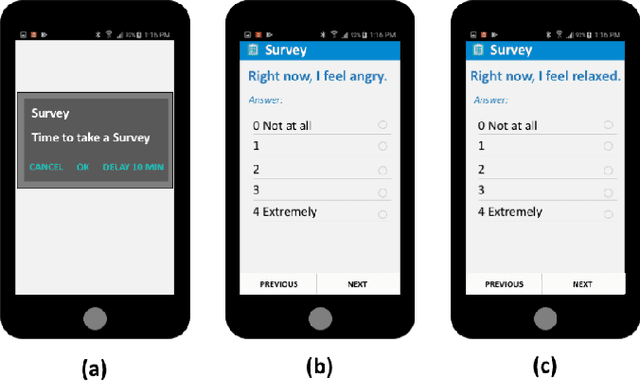
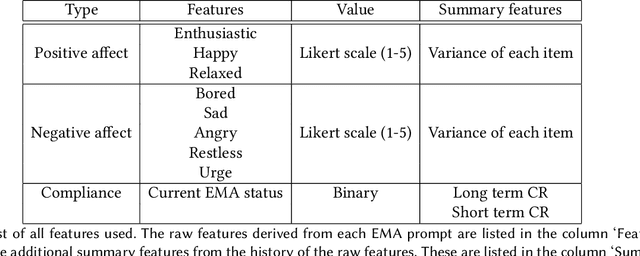
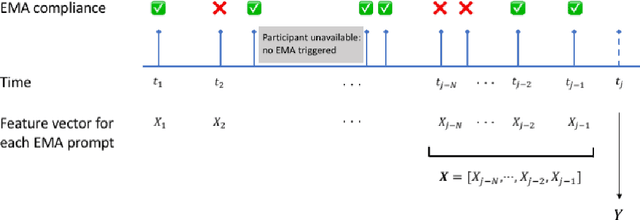
Ecological Momentary Assessments (EMAs) are an important psychological data source for measuring current cognitive states, affect, behavior, and environmental factors from participants in mobile health (mHealth) studies and treatment programs. Non-response, in which participants fail to respond to EMA prompts, is an endemic problem. The ability to accurately predict non-response could be utilized to improve EMA delivery and develop compliance interventions. Prior work has explored classical machine learning models for predicting non-response. However, as increasingly large EMA datasets become available, there is the potential to leverage deep learning models that have been effective in other fields. Recently, transformer models have shown state-of-the-art performance in NLP and other domains. This work is the first to explore the use of transformers for EMA data analysis. We address three key questions in applying transformers to EMA data: 1. Input representation, 2. encoding temporal information, 3. utility of pre-training on improving downstream prediction task performance. The transformer model achieves a non-response prediction AUC of 0.77 and is significantly better than classical ML and LSTM-based deep learning models. We will make our a predictive model trained on a corpus of 40K EMA samples freely-available to the research community, in order to facilitate the development of future transformer-based EMA analysis works.

Efficient Learning and Decoding of the Continuous-Time Hidden Markov Model for Disease Progression Modeling

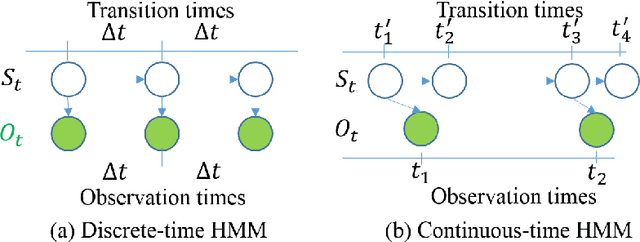
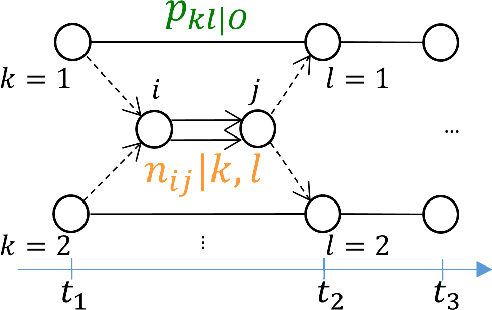
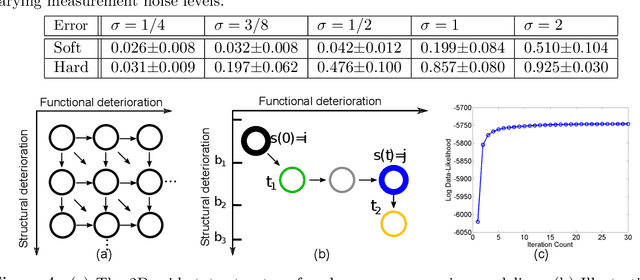
The Continuous-Time Hidden Markov Model (CT-HMM) is an attractive approach to modeling disease progression due to its ability to describe noisy observations arriving irregularly in time. However, the lack of an efficient parameter learning algorithm for CT-HMM restricts its use to very small models or requires unrealistic constraints on the state transitions. In this paper, we present the first complete characterization of efficient EM-based learning methods for CT-HMM models, as well as the first solution to decoding the optimal state transition sequence and the corresponding state dwelling time. We show that EM-based learning consists of two challenges: the estimation of posterior state probabilities and the computation of end-state conditioned statistics. We solve the first challenge by reformulating the estimation problem as an equivalent discrete time-inhomogeneous hidden Markov model. The second challenge is addressed by adapting three distinct approaches from the continuous time Markov chain (CTMC) literature to the CT-HMM domain. Additionally, we further improve the efficiency of the most efficient method by a factor of the number of states. Then, for decoding, we incorporate a state-of-the-art method from the (CTMC) literature, and extend the end-state conditioned optimal state sequence decoding to the CT-HMM case with the computation of the expected state dwelling time. We demonstrate the use of CT-HMMs with more than 100 states to visualize and predict disease progression using a glaucoma dataset and an Alzheimer's disease dataset, and to decode and visualize the most probable state transition trajectory for individuals on the glaucoma dataset, which helps to identify progressing phenotypes in a comprehensive way. Finally, we apply the CT-HMM modeling and decoding strategy to investigate the progression of language acquisition and development.