Yu-Ying Liu
Efficient Learning and Decoding of the Continuous-Time Hidden Markov Model for Disease Progression Modeling
Oct 26, 2021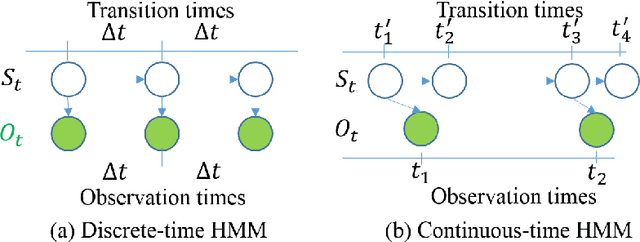

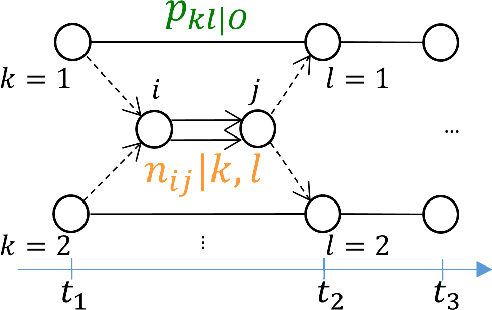
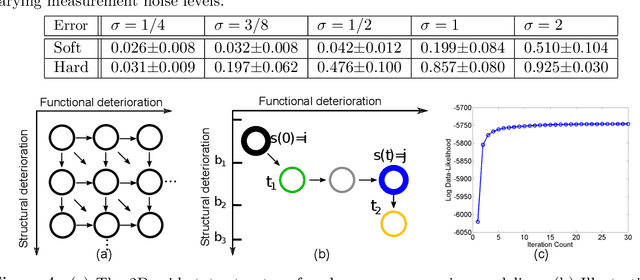
Abstract:The Continuous-Time Hidden Markov Model (CT-HMM) is an attractive approach to modeling disease progression due to its ability to describe noisy observations arriving irregularly in time. However, the lack of an efficient parameter learning algorithm for CT-HMM restricts its use to very small models or requires unrealistic constraints on the state transitions. In this paper, we present the first complete characterization of efficient EM-based learning methods for CT-HMM models, as well as the first solution to decoding the optimal state transition sequence and the corresponding state dwelling time. We show that EM-based learning consists of two challenges: the estimation of posterior state probabilities and the computation of end-state conditioned statistics. We solve the first challenge by reformulating the estimation problem as an equivalent discrete time-inhomogeneous hidden Markov model. The second challenge is addressed by adapting three distinct approaches from the continuous time Markov chain (CTMC) literature to the CT-HMM domain. Additionally, we further improve the efficiency of the most efficient method by a factor of the number of states. Then, for decoding, we incorporate a state-of-the-art method from the (CTMC) literature, and extend the end-state conditioned optimal state sequence decoding to the CT-HMM case with the computation of the expected state dwelling time. We demonstrate the use of CT-HMMs with more than 100 states to visualize and predict disease progression using a glaucoma dataset and an Alzheimer's disease dataset, and to decode and visualize the most probable state transition trajectory for individuals on the glaucoma dataset, which helps to identify progressing phenotypes in a comprehensive way. Finally, we apply the CT-HMM modeling and decoding strategy to investigate the progression of language acquisition and development.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge