Non-Stationary Latent Auto-Regressive Bandits
Paper and Code
Feb 05, 2024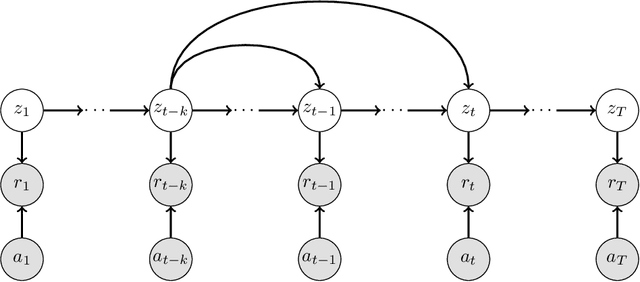
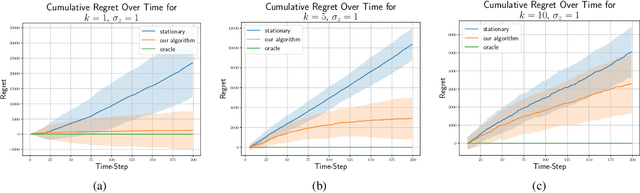
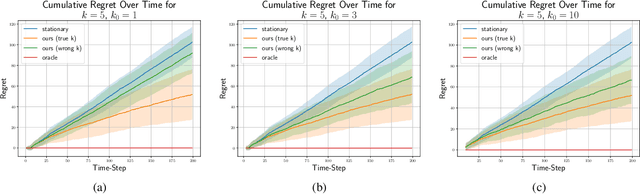
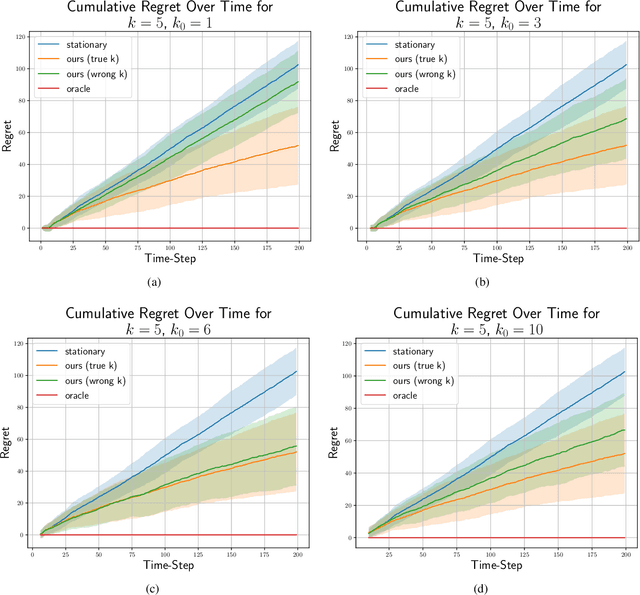
We consider the stochastic multi-armed bandit problem with non-stationary rewards. We present a novel formulation of non-stationarity in the environment where changes in the mean reward of the arms over time are due to some unknown, latent, auto-regressive (AR) state of order $k$. We call this new environment the latent AR bandit. Different forms of the latent AR bandit appear in many real-world settings, especially in emerging scientific fields such as behavioral health or education where there are few mechanistic models of the environment. If the AR order $k$ is known, we propose an algorithm that achieves $\tilde{O}(k\sqrt{T})$ regret in this setting. Empirically, our algorithm outperforms standard UCB across multiple non-stationary environments, even if $k$ is mis-specified.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge