Robust Out-of-Order Retrieval for Grid-Based Storage at Maximum Capacity

This paper proposes a framework for improving the operational efficiency of automated storage systems under uncertainty. It considers a 2D grid-based storage for uniform-sized loads (e.g., containers, pallets, or totes), which are moved by a robot (or other manipulator) along a collision-free path in the grid. The loads are labeled (i.e., unique) and must be stored in a given sequence, and later be retrieved in a different sequence -- an operational pattern that arises in logistics applications, such as last-mile distribution centers and shipyards. The objective is to minimize the load relocations to ensure efficient retrieval. A previous result guarantees a zero-relocation solution for known storage and retrieval sequences, even for storage at full capacity, provided that the side of the grid through which loads are stored/retrieved is at least 3 cells wide. However, in practice, the retrieval sequence can change after the storage phase. To address such uncertainty, this work investigates \emph{$k$-bounded perturbations} during retrieval, under which any two loads may depart out of order if they are originally at most $k$ positions apart. We prove that a $Θ(k)$ grid width is necessary and sufficient for eliminating relocations at maximum capacity. We also provide an efficient solver for computing a storage arrangement that is robust to such perturbations. To address the higher-uncertainty case where perturbations exceed $k$, a strategy is introduced to effectively minimize relocations. Extensive experiments show that, for $k$ up to half the grid width, the proposed storage-retrieval framework essentially eliminates relocations. For $k$ values up to the full grid width, relocations are reduced by $50\%+$.

High-Performance Dual-Arm Task and Motion Planning for Tabletop Rearrangement

We propose Synchronous Dual-Arm Rearrangement Planner (SDAR), a task and motion planning (TAMP) framework for tabletop rearrangement, where two robot arms equipped with 2-finger grippers must work together in close proximity to rearrange objects whose start and goal configurations are strongly entangled. To tackle such challenges, SDAR tightly knit together its dependency-driven task planner (SDAR-T) and synchronous dual-arm motion planner (SDAR-M), to intelligently sift through a large number of possible task and motion plans. Specifically, SDAR-T applies a simple yet effective strategy to decompose the global object dependency graph induced by the rearrangement task, to produce more optimal dual-arm task plans than solutions derived from optimal task plans for a single arm. Leveraging state-of-the-art GPU SIMD-based motion planning tools, SDAR-M employs a layered motion planning strategy to sift through many task plans for the best synchronous dual-arm motion plan while ensuring high levels of success rate. Comprehensive evaluation demonstrates that SDAR delivers a 100% success rate in solving complex, non-monotone, long-horizon tabletop rearrangement tasks with solution quality far exceeding the previous state-of-the-art. Experiments on two UR-5e arms further confirm SDAR directly and reliably transfers to robot hardware.

Fully Packed and Ready to Go: High-Density, Rearrangement-Free, Grid-Based Storage and Retrieval

Grid-based storage systems with uniformly shaped loads (e.g., containers, pallets, totes) are commonplace in logistics, industrial, and transportation domains. A key performance metric for such systems is the maximization of space utilization, which requires some loads to be placed behind or below others, preventing direct access to them. Consequently, dense storage settings bring up the challenge of determining how to place loads while minimizing costly rearrangement efforts necessary during retrieval. This paper considers the setting involving an inbound phase, during which loads arrive, followed by an outbound phase, during which loads depart. The setting is prevalent in distribution centers, automated parking garages, and container ports. In both phases, minimizing the number of rearrangement actions results in more optimal (e.g., fast, energy-efficient, etc.) operations. In contrast to previous work focusing on stack-based systems, this effort examines the case where loads can be freely moved along the grid, e.g., by a mobile robot, expanding the range of possible motions. We establish that for a range of scenarios, such as having limited prior knowledge of the loads' arrival sequences or grids with a narrow opening, a (best possible) rearrangement-free solution always exists, including when the loads fill the grid to its capacity. In particular, when the sequences are fully known, we establish an intriguing characterization showing that rearrangement can always be avoided if and only if the open side of the grid (used to access the storage) is at least 3 cells wide. We further discuss useful practical implications of our solutions.

PROBE: Proprioceptive Obstacle Detection and Estimation while Navigating in Clutter

In critical applications, including search-and-rescue in degraded environments, blockages can be prevalent and prevent the effective deployment of certain sensing modalities, particularly vision, due to occlusion and the constrained range of view of onboard camera sensors. To enable robots to tackle these challenges, we propose a new approach, Proprioceptive Obstacle Detection and Estimation while navigating in clutter PROBE, which instead relies only on the robot's proprioception to infer the presence or absence of occluded rectangular obstacles while predicting their dimensions and poses in SE(2). The proposed approach is a Transformer neural network that receives as input a history of applied torques and sensed whole-body movements of the robot and returns a parameterized representation of the obstacles in the environment. The effectiveness of PROBE is evaluated on simulated environments in Isaac Gym and with a real Unitree Go1 quadruped robot.

Optimally Solving Colored Generalized Sliding-Tile Puzzles: Complexity and Bounds

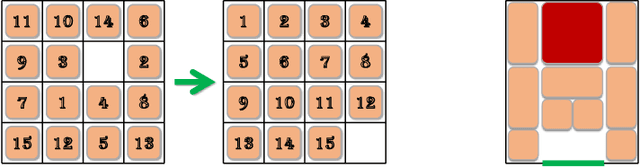
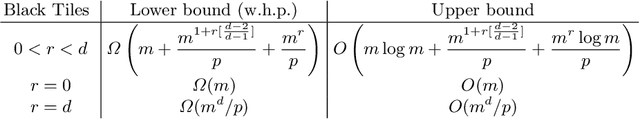
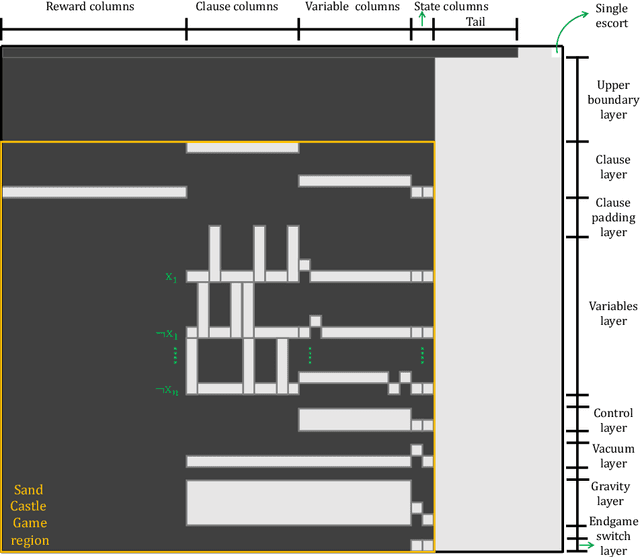
The Generalized Sliding-Tile Puzzle (GSTP), allowing many square tiles on a board to move in parallel while enforcing natural geometric collision constraints on the movement of neighboring tiles, provide a high-fidelity mathematical model for many high-utility existing and future multi-robot applications, e.g., at mobile robot-based warehouses or autonomous garages. Motivated by practical relevance, this work examines a further generalization of GSTP called the Colored Generalized Sliding-Tile Puzzle (CGSP), where tiles can now assume varying degrees of distinguishability, a common occurrence in the aforementioned applications. Our study establishes the computational complexity of CGSP and its key sub-problems under a broad spectrum of possible conditions and characterizes solution makespan lower and upper bounds that differ by at most a logarithmic factor. These results are further extended to higher-dimensional versions of the puzzle game.

Asymptotically-Optimal Multi-Query Path Planning for Moving A Convex Polygon in 2D

The classical shortest-path roadmaps, also known as reduced visibility graphs, provide a multi-query method for quickly computing optimal paths in two-dimensional environments. Combined with Minkowski sum computations, shortest-path roadmaps can compute optimal paths for a translating robot in 2D. In this study, we explore the intuitive idea of stacking up a set of reduced visibility graphs at different orientations for a convex-shaped holonomic robot, to support the fast computation of near-optimal paths allowing simultaneous 2D translation and rotation. The resulting algorithm, rotation-stacked visibility graph (RVG), is shown to be resolution-complete and asymptotically optimal. RVG out-performs SOTA single-query sampling-based methods including BIT* and AIT* on both computation time and solution optimality fronts.

Expected $1.x$-Makespan-Optimal MAPF on Grids in Low-Poly Time

Multi-Agent Path Finding (MAPF) is NP-hard to solve optimally, even on graphs, suggesting no polynomial-time algorithms can compute exact optimal solutions for them. This raises a natural question: How optimal can polynomial-time algorithms reach? Whereas algorithms for computing constant-factor optimal solutions have been developed, the constant factor is generally very large, limiting their application potential. In this work, among other breakthroughs, we propose the first low-polynomial-time MAPF algorithms delivering $1$-$1.5$ (resp., $1$-$1.67$) asymptotic makespan optimality guarantees for 2D (resp., 3D) grids for random instances at a very high $1/3$ agent density, with high probability. Moreover, when regularly distributed obstacles are introduced, our methods experience no performance degradation. These methods generalize to support $100\%$ agent density. Regardless of the dimensionality and density, our high-quality methods are enabled by a unique hierarchical integration of two key building blocks. At the higher level, we apply the labeled Grid Rearrangement Algorithm (RTA), capable of performing efficient reconfiguration on grids through row/column shuffles. At the lower level, we devise novel methods that efficiently simulate row/column shuffles returned by RTA. Our implementations of RTA-based algorithms are highly effective in extensive numerical evaluations, demonstrating excellent scalability compared to other SOTA methods. For example, in 3D settings, \rta-based algorithms readily scale to grids with over $370,000$ vertices and over $120,000$ agents and consistently achieve conservative makespan optimality approaching $1.5$, as predicted by our theoretical analysis.

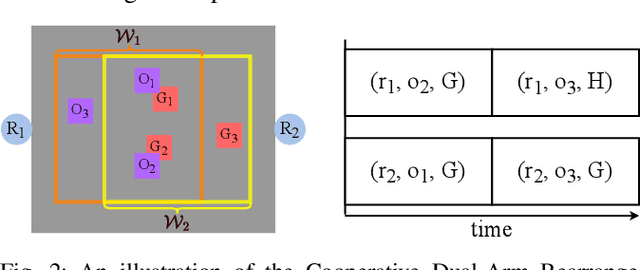
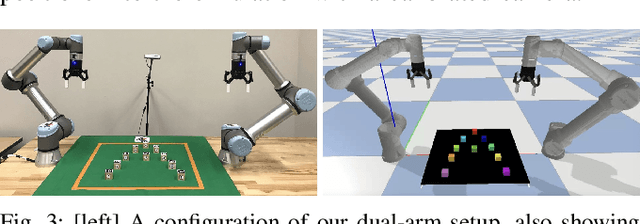
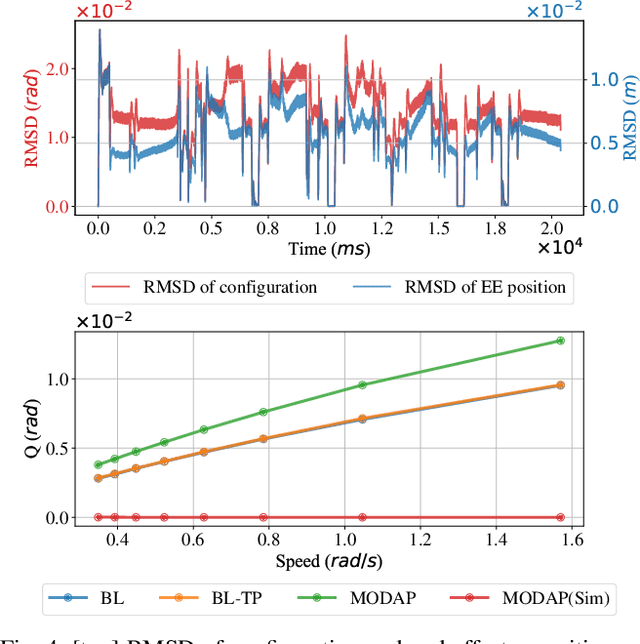
Toward Holistic Planning and Control Optimization for Dual-Arm Rearrangement

Long-horizon task and motion planning (TAMP) is notoriously difficult to solve, let alone optimally, due to the tight coupling between the interleaved (discrete) task and (continuous) motion planning phases, where each phase on its own is frequently an NP-hard or even PSPACE-hard computational challenge. In this study, we tackle the even more challenging goal of jointly optimizing task and motion plans for a real dual-arm system in which the two arms operate in close vicinity to solve highly constrained tabletop multi-object rearrangement problems. Toward that, we construct a tightly integrated planning and control optimization pipeline, Makespan-Optimized Dual-Arm Planner (MODAP) that combines novel sampling techniques for task planning with state-of-the-art trajectory optimization techniques. Compared to previous state-of-the-art, MODAP produces task and motion plans that better coordinate a dual-arm system, delivering significantly improved execution time improvements while simultaneously ensuring that the resulting time-parameterized trajectory conforms to specified acceleration and jerk limits.

Decentralized Lifelong Path Planning for Multiple Ackerman Car-Like Robots

Path planning for multiple non-holonomic robots in continuous domains constitutes a difficult robotics challenge with many applications. Despite significant recent progress on the topic, computationally efficient and high-quality solutions are lacking, especially in lifelong settings where robots must continuously take on new tasks. In this work, we make it possible to extend key ideas enabling state-of-the-art (SOTA) methods for multi-robot planning in discrete domains to the motion planning of multiple Ackerman (car-like) robots in lifelong settings, yielding high-performance centralized and decentralized planners. Our planners compute trajectories that allow the robots to reach precise $SE(2)$ goal poses. The effectiveness of our methods is thoroughly evaluated and confirmed using both simulation and real-world experiments.

Well-Connected Set and Its Application to Multi-Robot Path Planning

Parking lots and autonomous warehouses for accommodating many vehicles/robots adopt designs in which the underlying graphs are \emph{well-connected} to simplify planning and reduce congestion. In this study, we formulate and delve into the \emph{largest well-connected set} (LWCS) problem and explore its applications in layout design for multi-robot path planning. Roughly speaking, a well-connected set over a connected graph is a set of vertices such that there is a path on the graph connecting any pair of vertices in the set without passing through any additional vertices of the set. Identifying an LWCS has many potential high-utility applications, e.g., for determining parking garage layout and capacity, as prioritized planning can be shown to be complete when start/goal configurations belong to an LWCS. In this work, we establish that computing an LWCS is NP-complete. We further develop optimal and near-optimal LWCS algorithms, with the near-optimal algorithm targeting large maps. A complete prioritized planning method is given for planning paths for multiple robots residing on an LWCS.