Optimally Solving Colored Generalized Sliding-Tile Puzzles: Complexity and Bounds

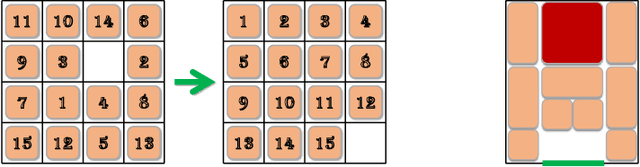
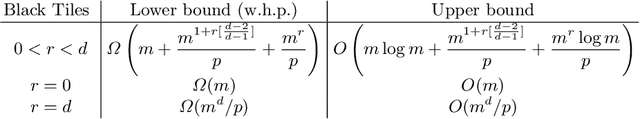
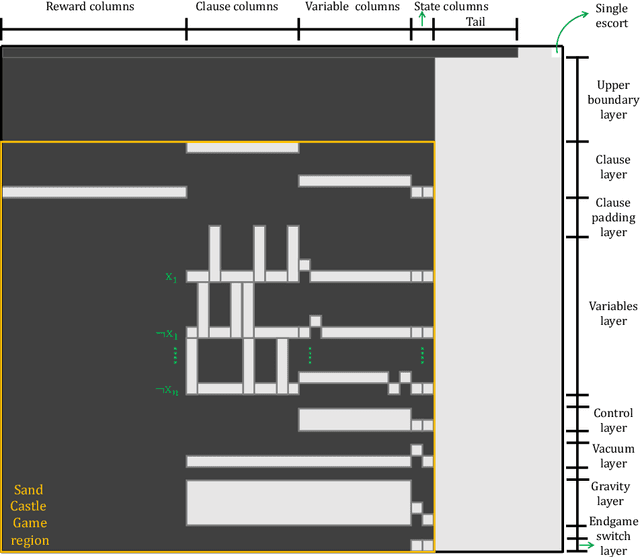
The Generalized Sliding-Tile Puzzle (GSTP), allowing many square tiles on a board to move in parallel while enforcing natural geometric collision constraints on the movement of neighboring tiles, provide a high-fidelity mathematical model for many high-utility existing and future multi-robot applications, e.g., at mobile robot-based warehouses or autonomous garages. Motivated by practical relevance, this work examines a further generalization of GSTP called the Colored Generalized Sliding-Tile Puzzle (CGSP), where tiles can now assume varying degrees of distinguishability, a common occurrence in the aforementioned applications. Our study establishes the computational complexity of CGSP and its key sub-problems under a broad spectrum of possible conditions and characterizes solution makespan lower and upper bounds that differ by at most a logarithmic factor. These results are further extended to higher-dimensional versions of the puzzle game.

On Computing Makespan-Optimal Solutions for Generalized Sliding-Tile Puzzles

In the $15$-puzzle game, $15$ labeled square tiles are reconfigured on a $4\times 4$ board through an escort, wherein each (time) step, a single tile neighboring it may slide into it, leaving the space previously occupied by the tile as the new escort. We study a generalized sliding-tile puzzle (GSTP) in which (1) there are $1+$ escorts and (2) multiple tiles can move synchronously in a single time step. Compared with popular discrete multi-agent/robot motion models, GSTP provides a more accurate model for a broad array of high-utility applications, including warehouse automation and autonomous garage parking, but is less studied due to the more involved tile interactions. In this work, we analyze optimal GSTP solution structures, establishing that computing makespan-optimal solutions for GSTP is NP-complete and developing polynomial time algorithms yielding makespans approximating the minimum with expected/high probability constant factors, assuming randomized start and goal configurations.