Safe Feedback Motion Planning: A Contraction Theory and $\mathcal{L}_1$-Adaptive Control Based Approach
Paper and Code
Apr 02, 2020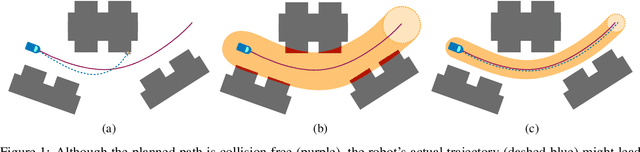
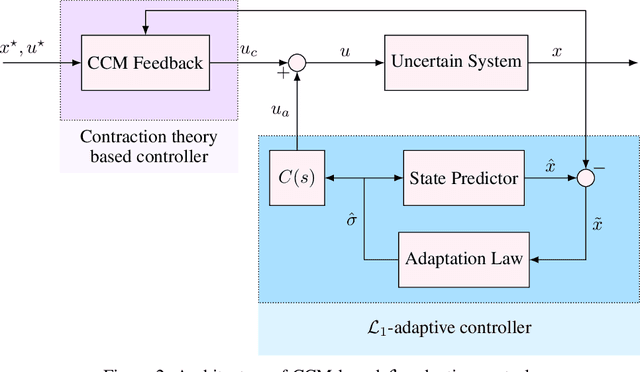
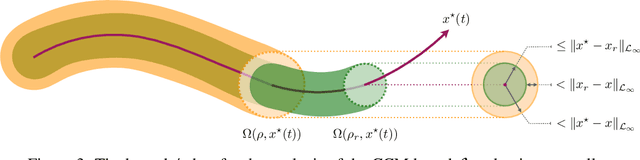
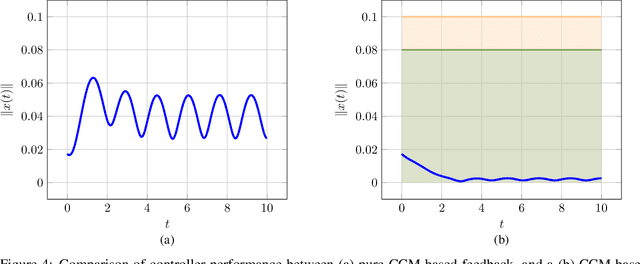
Autonomous robots that are capable of operating safely in the presence of imperfect model knowledge or external disturbances are vital in safety-critical applications. In this paper, we present a planner-agnostic framework to design and certify safe tubes around desired trajectories that the robot is always guaranteed to remain inside of. By leveraging recent results in contraction analysis and $\mathcal{L}_1$-adaptive control we synthesize an architecture that induces safe tubes for nonlinear systems with state and time-varying uncertainties. We demonstrate with a few illustrative examples how contraction theory-based $\mathcal{L}_1$-adaptive control can be used in conjunction with traditional motion planning algorithms to obtain provably safe trajectories.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge